PSO算法优化BP神经网络的EIT图像重建算法

谢莉莉，汪 鹏，陈 丽

XIE Li-li1，WANG Peng2，CHEN Li3

（1.天津职业大学 电子信息工程学院，天津 300410；2.河北工业大学 计算机科学与软件学院，天津 300401；

3.河北工程大学 信息与电气工程学院，邯郸 056038）

0 引言

电阻抗成像（EIT）是利用对物体表面的电测量来重建反映物体内部结构及功能变化图像的一种新颖的计算机影像技术。EIT在工业监测、无损探伤等方面也引起工业界极大关注[1]。EIT的实现一般是通过在物体表面设置一定数量的电极，在选定的电极上施加一定模式的电流，然后测量各电极的电压，再将这些已知的电流、电压数据，依据图象重建算法，构造出物体内部的未知阻抗图像[2]。

我们构造了一套实时电阻抗成像的实验系统，系统具有32个电极，采用相邻电极注入电流及相邻电极测量电压采集。如图1所示，不同模式的电流由恒流源通过多路选择开关施加到物体表面电极，由高精度的A/D采集模块通过多路选择开关采集各相邻电极的电压数据，最后由微控制器（51单片机）将数据预处理并控制传输给计算机，再重建出阻抗分布图像。

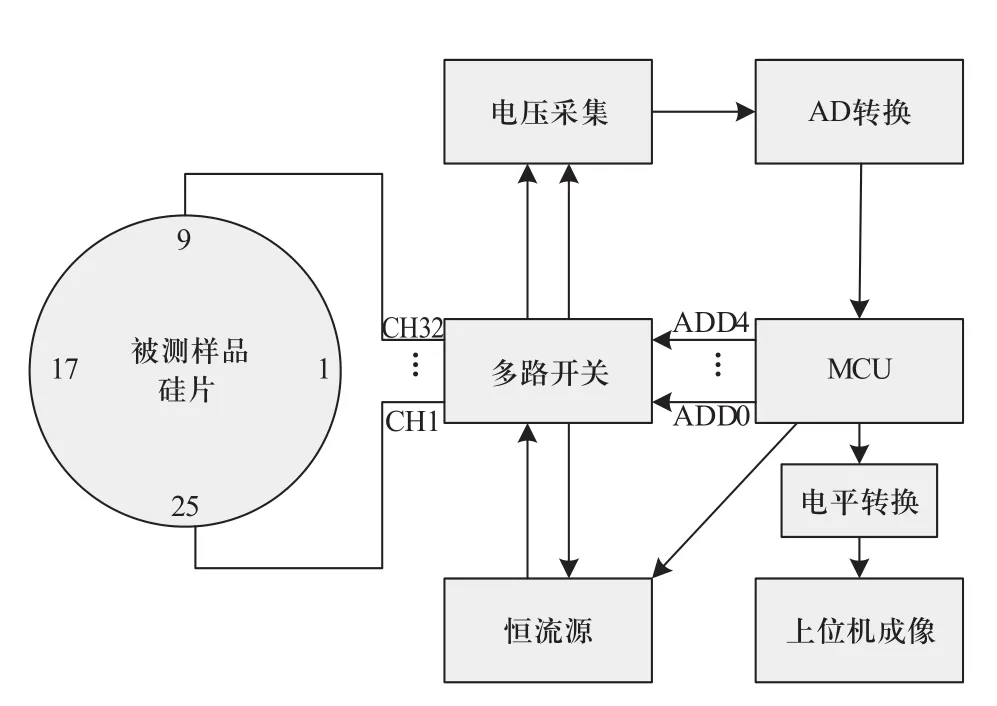
图1 采集系统结构图

EIT图象重建是一个高度病态、非线性的反问题，它是目前EIT技术中关键的研究课题。目前成像算法主要分为基于非迭代的线性动态成像和基于迭代的非线性静态成像两类[3]。最早由Barber和 Brown提出的反投影重建算法，是目前唯一应用于临床的算法，尽管这种算法有很好的鲁棒性，但成像分辨率和对比度太差。Newton-Raphson法是基于非线性迭代的静态成像技术，被普遍认为是目前EIT图像重建最有成效的方法，但是这些方法实现起来相当复杂，成像速度慢，达不到临床成像的要求。另外有文献提出了基于线性神经网络的成像方法，但这些方法不能适应EIT中复杂的病态非线性特性。有些文献提出了基于BP神经网络的成像方法，但由于BP网络本身的缺点造成成像速度慢，成像效果不佳。

基于PSO优化BP神经网络的方法进行EIT图像重建是在基本BP神经网络结构的基础上，再引入PSO算法进行权值修正。不仅能很好地适应EIT的病态非线性特性，而且可以克服基本BP算法收敛速度慢和易陷于局部极值的局限。该方法较好地提高了BP神经网络学习能力及泛化能力。

1 EIT图像重建数学模型

如图2所示，在二维场中，设被测物场区域为D，D的边界为∂D。D内阻抗分布为ρ（x，y），电位分布为 φ（x，y），由于场内没有电流源和电流汇，满足Laplace方程[4]：

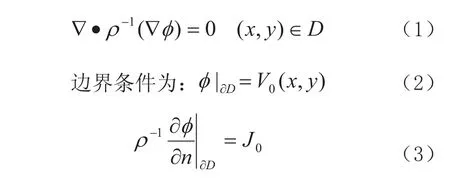
公式中 为Laplace 算子，V0为边界处的测量电压，J0为边界处的电流密度，∂D为区域边界，n是边界外法线方向。EIT问题就是从已知边界处的J0和V0求解阻抗分布ρ。它是一个非线性的反问题，在求解反问题的过程中又涉及到求解正问题。所谓正问题就是已知阻抗分布ρ和激励电流模式J0计算出电位分布φ。在现有的EIT图象重建方法中对正问题的求解均借助于有限元方法（FEM），对反问题的求解通常使用迭代的方法。

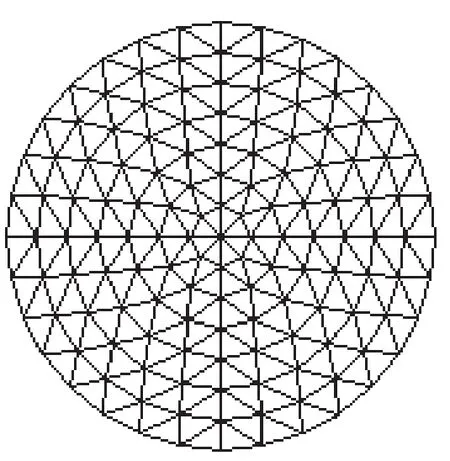
图2 圆形样品

2 BP-PSO实现EIT图像重建

BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层（hide layer）和输出层（output layer）。

粒子群算法（Particle Swarm Optimization，PSO）是模拟鸟类觅食行为的一种启发式搜索方法[5]。PSO算法使用下面公式（7）和（8）更新空间位置和速度。每代粒子根据适应度函数得到最优粒子，经过若干次迭代后最优粒子即为所求最优解。

2.1 神经网络构造及参数设置

将圆形样品均匀剖分成7层，如图2所示，共141个节点、248个单元。最外层有32个节点，将32个电极均匀放置在外层32个节点上。采用相邻电极驱动及相邻电极测量，进行32轮电流注入，每轮可获得29个独立边界电压，共928个数据。

根据图3所示的网络结构，设置网络，928个测量数据对应输入层的输入信息个数m，248个单元对应输出层的输出信息个数q。设置隐含层节点个数n为248个。连接权值和阈值学习参数α＝ β＝0.6。PSO搜索空间维数（BP网络权值和阈值数目）：D＝m×n＋n×q＋n＋q。PSO算法的最小适应度（最小训练停止误差）γ＝10－6；PSO的学习因子c1＝c2＝2；惯性权值u＝1.0；PSO算法初始群体个体数目设为50；最大迭代遍数T＝1000；PSO初始样本生成：随机初始化50*D个初始值。

2.2 神经网络样本的产生

随机生成100个样本，每个样本的期望输出采用有限元法计算。先随机生成每个样本的输出（248个单元的电导率），再利用有限元法计算出928个边界电压值，作为一个样本。

2.3 用PSO训练神经网络过程

根据神经网络输出层单元的新激活值计算公式计算出每个粒子坐标所对应的神经网络的输出O，假设期望输出为A（O 和A均为q×1维向量），代入适应度函数：

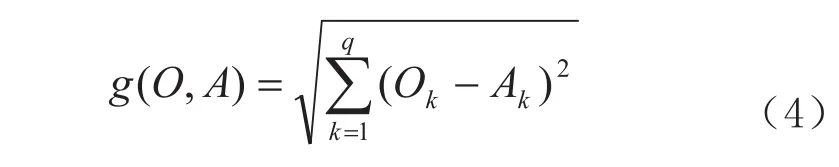
式中，Ok和Ak分别为输出层第k个单元的实际输出值和期望输出值。

PSO算法优化的目标，就是找到这样一个粒子坐标（BP神经网络的权值和阈值），使得适应度函数得到最小值。

POS算法的过程为：首先初始化粒子群坐标Xi和速度Vi；初始化Pi＝Xi。根据公式（4）计算所有粒子的适应度，并将取得最小适应度的粒子坐标付给Pg。

3 重建图像及结论

根据以上论述建立BP神经网络，用PSO算法对网络权值和阈值进行优化训练，重建圆形样品的电导率分布，成像结果如图3所示。

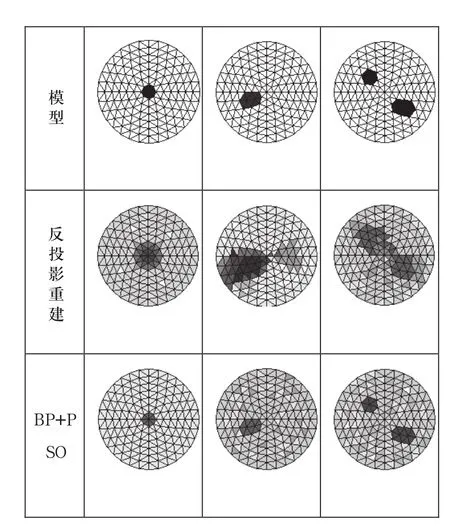
图3 不同算法的电阻抗成像效果

由图像重建方法及重建结果得到如下结论：

1）图像的质量及神经网络的泛化能力与输入输出的样本对数有直接关系，样本越多效果越好。

2）采用BP-PSO的EIT图像重建算法，可离线充分训练，可使成像速度提高，其速度要优于动态反投影重建算法及静态成像算法。

3）在样品区域中的不同位置改变电导率，该算法的成像效果要优于反投影重建算法。

4）基于PSO优化BP神经网络的方法，较其它基于神经网络的EIT图像重建方法收敛速度更快并且不易陷于局部极值。

[1]Cheney M.Electrical impedance tomography [J].S IAM Review，1999，41（1）：85-101．

[2]Bertrand M，Boulay C，Guardo R,et al.An experimental study in electrical impedance tomography using backprojection reconstruction.IEEE Trans Biomed Eng，1991；38（7）：617.

[3]Jan C de Munck，Theo J C Faes，Rob M Heethaar.The Boundary Element Method in the Forward and Inverse Problem of Electrical Impedance Tomography[J].IEEE Trans Biomed Eng 2000,47（6）：792-800.

[4]Webster J G（Ed）.Electrical Impedance Tomography.Bristol,England：Adam.Hilger,1990：1-205.

[5]SECRESTBR，LAMONT G B.Visualizing Particle Swarm optimization.In Proceedings of the 2003 IEEE Swarm Intelligence Symposium，SIS’03.Indianapolis（IN，USA）：2003.198-204.