基于矢量阵测量的局部近场全息技术研究
胡 博,杨德森
(哈尔滨工程大学 水声工程学院,哈尔滨 150001)
近场声全息技术[1-3](NAH)是上世纪80年代由全息领域脱颖而出的一项全息成像技术。相对于传统全息技术,在测量系统的动态范围选取适当的情况下,NAH技术不仅可以重建出空间点上的声压标量,还可以获得空间点的质点振速、声强等矢量,以及远场指向性等重要声学信息。因此基于以上特点,NAH技术被广泛应用于噪声源的识别与应用,特别是低频场源特性判别,结构振动的声辐射、声散射等问题的研究统计最优近场声全息技术[4](SONAH)是 Patch NAH技术中一种典型的算法,它不存在卷积运算,所以可以从根本上解决困扰传统NAH技术的窗效应和卷绕误差[5,6]。对于该算法,国内外的学者都进行了一系列的研究。其中,Cho等人[7]将SONAH算法推广到柱面坐标系中,实现了对圆柱体辐射声场的重建,拓展了算法应用范围。Hald等人[8]又基于双全息面测量,成功地将改进的SONAH用于封闭环境声场的重建。合肥工业大学的李卫兵等人[9]提出了适用于统计最优平面近场声全息的双平面测量的空间声场分离技术,该技术可以准确地分离出全息面两侧声源分别在每个全息面上产生的声压,进而通过分离声压来重建声源面上的各种声学量,从而可以实现全息面两侧均有声源的声场重建与预测。
虽然国内外对该方法很关注,但都只局限于使用声压信息进行处理,而淡忘了振速这个同样带有声场信息的量。近几年的研究发现[10],在近场声全息数据的测量过程中,如果利用质点振速进行声场重构,重构效果要比声压测量的效果理想。同时,在水声测量仪器方面,人们也只限于使用声压水听器,虽然测量结果也十分准确,但测量所需水听器数量多,工作量大,耗时长,在如此长的时间内,声源的辐射声场有可能发生变化。因此,如果能使用一种更加便捷的测量仪器同时得到声压和振速,并找到一种更加有效的算法能够利用二者的关联和差别,对它们进行联合处理,使得信息处理系统具有更多的途径和方法来实现声场重构,一定会较以往的测量方法具有更大的优越性,这也会为解决一系列的声全息重构和测量问题提供新的解决办法。
为此,本文在统计最优柱面近场声全息技术的基础上,主要推导了基于振速重构的SONAH技术的基本公式,通过仿真把该方法与基于声压测量的处理效果相比较,突出其重构特点,结果表明理论推导的正确性及适用性。最后本文设计矢量阵进行了水池近场声全息实验研究,通过实验研究验证该算法的正确性及矢量阵用于近场声全息测量的可行性,为该技术的实际应用提供了理论依据。
1 基本原理
1.1 基于声压测量的全息重建公式
根据文献[4]中的定义,定义由波数矢量K=(n,kz)确定的半径为r的柱面上的空间频率域单元柱面波为:

假设rHn=(rH,θn,zn)(n=1,2,…,N)为全息柱面上N个声压测量点,rS=(rS,θ,z)为重构面上对应的重构点。根据波场的叠加原理可知:重建柱面上任意点处波数矢量的单元柱面波只能由全息面上所有点处的波数矢量Km的单元柱面波叠加而得到,即:

式中N为全息柱面压测量点数,M为重建柱面和全息柱面上复声压所包含的单元柱面波的数目,Cn(rS)为叠加系数。令:

其中,p(rS,θ,z)为柱坐标下的声压,再由式(2),确定的M个线性方程所构成的方程组:

并且为了保证方程组具有唯一解,必须要求M≥N,则方程组可以表示为:
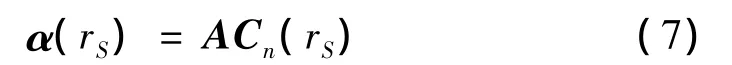
为了得到系数矩阵Cn(rS),可以通过正则化法来抑制小幅度倏逝波的影响,可得上式的正则化解为:

式中AH为矩阵A的共轭转置矩阵,θ为正则化参数,I为单位对角矩阵。文献[4]中给出了一定条件下,根据信噪比来确定正则化参数θ的公式:

式中:d为重构面距离,SNR未包含所有随机误差和噪声的信噪比。将式(8)带入(3)中,得到:

式中:pT=[p(rH1),…,p(rHN)],pT为 p的转置。由欧拉公式,同样可得到重构径向振速结果:
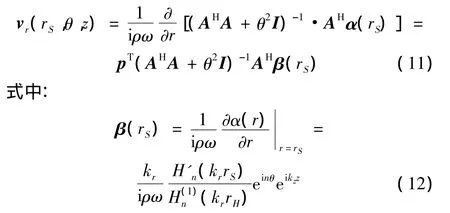
1.2 基于振速测量的全息重建公式
由欧拉公式,可以得到:

式中 Vn(kz,r)是径向振速 vr(r,θ,z)的二维傅氏变换。与上一节的推导过程相同,根据波场的叠加原理,同理可以得到基于质点振速测量的柱面SONAH技术的重建公式为:

然后,还可以得到基于径向振速测量的复声压重构公式为:

以上推导了基于振速测量的统计最优柱面近场声全息技术的基本公式。由式(14)和式(15)可以通过测量质点径向振速,可以得到柱面上任意点处的复声压和径向振速。
2 仿真验证
利用MATLAB软件编制程序进行数值仿真,验证该算法的有效性和可行性。假设在柱坐标系中,以柱体的中心为坐标原点,圆柱的中心轴为z坐标轴,柱坐标系中在原点处有一单极子点源,振源频率为1 000 Hz,全息柱面半径rH=0.25 m,重构柱面半径rS=0.24 m,两圆柱体的高均为L=2 m,轴向和周向的采样点数都为10,水中声速c=1 500 m/s,水密度ρ=1 000 kg/m3。为方便起见,只画出了柱面上θ=0母线上的声压及径向振速幅值,而对于基于声压和基于质点振速重构的SONAH技术,我们在这里简称为声压法和质点振速法。为了更详细地比较重构效果,定义相对幅值误差ε为:

式中:are为重构柱面上声压或径向振速的理论值,al是重构柱面上声压或径向振速重建值。
首先验证理论的正确性,为了突出SONAH技术在处理有限全息孔径方面的优势,在不同全息柱面高度的条件下比较重构效果,结果如图1所示。需要说明的是,这里之所以只改变全息柱面高度而不改变全息柱面半径,主要是因为全息柱面的特殊性,即改变全息柱面半径的同时全息距离也会随之变化,这使得全息面大小在周向的选取必须考虑重建距离的影响,所以本文只考察柱体高度对重构结果的影响。

图1 不同全息柱面高度时的重构效果Fig.1 Comparison of reconstructed results of different ZH
从图1中可以看到,当全息柱面高度与重构柱面高度之比ZH/ZS分别为2、1和0.5的条件下,无论是对于声压法还是质点振速法,SONAH技术都能识别出声源的位置和声辐射的大小,能够达到预期的声源识别目的,经计算当ZH/ZS=0.5时声压幅值误差和径向振速幅值误差最小分别为-27.3 dB和-25.6 dB,而如果采用文献[10]中的传统基于空间声场变换的近场声全息技术,两误差分别为-12.5 dB和-11.9 dB,这就验证了SONAH技术可以从根本上解决窗效应和卷绕误差,并且对测量孔径面积的要求没有基于空间声场变换的近场声全息技术那么严格,可以很方便地实现空间声场重建的特点;对于重构的声压结果,声压法得到的结果较好,符合理论值的分布规律,对于重构的径向振速结果则正好相反,质点振速法得到的重构效果最好,这不仅体现在其结果分布基本符合点源声场的声辐射特性,同时在边缘处振速法的衰减速度更快,不连续性较小,而声压法得到的重构结果与理论值存在很大的误差。

图2 不同全息距离时的重构误差Fig.2 Comparison of reconstructed errors of different d
进一步,改变全息距离考察全息距离d对重构效果的影响,结果如图2中所示。可以发现,随着d的增加,重构误差也随之增大,当d≤0.04 m时,误差曲线的上升斜率很大,误差随重构距离的增大变化很快,当d≥0.04 m时,曲线上升趋势趋于平缓。分析原因,主要是因为在全息柱面高度和重构柱面相同的条件下,改变重构距离d的同时柱体的半径也改变了,其结果使全息柱面的测量孔径也发生了变化,当d≥0.04 m时测量孔径增大到所带来的好处可以抵消一部分重构距离增大带来的误差,此时误差曲线的上升就会变得比较缓慢,这也验证了之前的分析结果。
3 实验研究
3.1 实验系统介绍
为检验以上理论,在消声水池采用矢量阵进行了水中声全息测量实验。水池的尺寸为4 m×3.6 m×3.6 m,可六面消声,消声频率 ≥3 kHz。整个实验系统由机械扫描系统、发射系统和数据采集系统三部分组成。


水池中装配的多自由度机械系统由微机控制,机械系统中两个行车可以在驱动电机的控制下分别进行上下、左右、前后及360°旋转的四自由度移动,平动扫描精度小于0.5 mm,旋转扫描精度小于0.2°,实验时矢量阵和发射换能器分别垂直固定在机械扫描系统的两个支架下方,实验系统布置如图3所示。发射端采用柱形换能器发射幅值为100 mV正弦波信号,数据采集系统由八元矢量水听器阵列、前置放大器、32通道可编程滤波放大器、PULSE多通道采集器和微机分析软件组成。其中,采集器的采样频率为32 kHz,功放的声压和振速放大量分别为40 dB和20 dB,声全息测量系统采用八元矢量水听器阵列,阵元间隔0.25 m,阵长1.75 m,使用前阵列经灵敏度校准,每只矢量水听器的测量频率范围为200 kHz~8 kHz,矢量阵如图4所示。

图5 六号水听器声传播衰减曲线Fig.5 Attenuation curve of No.6 vector sensor

表1 各水听器声压传播衰减量(dB/倍距离)Tab.1 Radiated attenuation of each vector sensor
由于矢量水听器测量的特殊要求使得在近场测量时,阵架及水听器之间的声散射现象可能会使测量值与真实信号间产生失真,因此在近场测量之前有必要对矢量阵的声散射影响进行检测。其具体检测方法在文献[11]中已有详细说明,这里不再赘述,经计算给出各水听器的每倍距离传播衰减量见表1,其中六号阵元的声压传播衰减曲线见图5。明显的,各个水听器的测量曲线满足球面波衰减规律,因此整个矢量阵作为近场测量是合适的。
实验时,矢量阵固定不动,发射换能器距矢量阵0.52 m,由微机控制进行周向旋转逐点测量,每次旋转角度为5°,由于一次扫描难以完成声场全部测量,因此采用调整发射换能器深度,垂直方向变深2次,每次移动0.08 m,进行插补测量。整个实验的测量点数为Nθ×Nz=72×24,Δz=0.08 m,Δθ=5°。数据采集后,进行了灵敏度补偿和放大量修正,再按空间位置关系重新排列数据顺序。
3.2 数据处理
采用柱面SONAH技术进行声场重建,研究柱体声源的辐射特性及重构面声压径向振速分布情况。为了突出该算法特点,使全息面与重构面尺寸相同,分别利用两种重构方法的柱体SONAH技术对获取数据进行重构,理论值及对比结果如图6所示。
图6给出了基于两种重构方法的统计最优法重构结果,由于声源位于原点,因此重构柱面的声场分布应该是对称的,在这里只给出了0≤θ≤π面的重构结果。对比发现:在全息柱面与重构面柱高度相同的情况下,SONAH技术同样能获得理想的重构效果,其重建的声场结果依然很好的延续全息面声场信息的分布趋势,在边缘处的振荡误差很小,能够实现声源的准确定位,这说明它的可信度还是很高的;对于重构声压和径向振速结果,声压法和振速法的仍然具有比较明显的优势,其处理结果与点声源辐射声场分布非常吻合,其中声压—声压的重构误差为-15.98 dB,振速—振速的重构误差为-15.42 dB;图中在2.4≤θ≤3范围内,重建的声场分布会出现一个突出点,这可能是由于测量位置误差或柱形发射换能器的表面振动不均匀产生的,具体原因还有待进一步研究。

图6 两种统计最优法的重构结果比较Fig.6 Comparison of reconstructed results of two SONAH methods
4 结论
本文研究了基于矢量阵测量的局部近场声全息技术,推导了基于振速重构的重构公式,在多种测量条件下,通过仿真计算讨论其适用条件,与其它方法对比分析,结果表明利用基于振速测量的SONAH技术具有很大的优势,可以进行局部近场声场重构,扩大了常规平面全息技术的应用范围。最后,设计了基于矢量阵测量的水池近场声全息实验,实验结果表明:本实验设计的八元矢量阵通过一次测量就能共点、同时测量声压和振速信息,不仅位置信息准确,而且获得的声场信息丰富,与传统声压测量法相比测量系统的复杂程度降低,测量效率明显提高,可以说矢量阵的采用为近场声全息技术的水中应用提供了方便和保障;验证了基于振速测量的SONAH算法的有效性,对于全息孔径有限的情况,该技术能够获得较高的重构精度,完全可以用于水中柱体的噪声源识别过程中。可以说本文的研究为柱面SONAH技术在实际工程中的应用提供了理论依据和实践基础,对于诸如电动机、火车等柱状或类柱状物体的噪声源识别和定位具有比较积极的意义。
[1]Williams E G.Continuation of acoustic near-field[J].J Acoust.Sco.Am.,2003,113:1273-1281.
[2]万 泉,蒋伟康.有关循环平稳近场声全息的重建参数的若干确定准则[J].振动与冲击,2008,27(9):17-19.
[3]张海滨,蒋伟康,薛玮飞,等.基于HELS法的多源相干声场重建研究[J].振动与冲击,2008,27(1):93-96.
[4] Hald J.Patch near-field acoustic holography using a new statistically optimal method[C].Proceedings of INTERNOISE 2003,2003,2203-2210.
[5]李卫兵,陈 剑,毕传兴,等.统计最优球面近场声全息在噪声源识别中的应用[J].振动工程学报,2004,17(S):958-961.
[6]杨 超,陈 进,李加庆,等.局部近场声全息的仿真与实验研究[J].振动与冲击,2007,26(12):138-140.
[7] Cho Y T, Bolton JS. Sourcevisualization byusing statistically optimized near-field acoustical holography in cylindrical coordinates[J].J Acoust.Soc.Am,2005,118(4):2355-2364.
[8]Hald J.Patch holography in cabin environments using a twolayer handheld array with an extended SONAH algorithm[C].Proceeding of Euro-noise 2006,Tampere,Finland.
[9]李卫兵,陈 剑,于 飞,等.统计最优平面近场声全息原理与声场分离技术[J].物理学报,2005,54(3):1253-1260.
[10] Jacobsen F,Liu Y.Near-field acoustic holography with particle velocity transducers[J].J Acoust.Soc.Am,2005,118(5):3139-3144.
[11]胡 博,杨德森,孙 玉.采用矢量阵测量的水中宽带近场声全息技术研究[J].振动与冲击,2010,29(5):29-33.

