基于提升小波包和模糊模式识别的结构有限元模型修正
谭冬梅,瞿伟廉
(武汉理工大学 道路桥梁与结构工程湖北省重点实验室,武汉 430070)
为了对土木工程结构进行损伤识别、健康诊断以及结构工作状态评估与预测,通常需要一个比较准确的有限元分析模型来了解结构的动力性能。然而,在建立大多数有限元模型过程中,都是根据结构设计图纸,采用较多的理想化假定和简化,由此有限元模型计算的结构动力特性和动力响应往往与现场实验结果存在一定的误差。当结构模态特性的实测值与有限元理论值之间存在较大的差异时,将导致模型计算结果与实际测量结果有较大出入,甚至会超出工程中所允许的精度。因此则需要对结构的有限元模型进行修正,使得结构模态特性的理论值趋近于实测值。目前己有的模型修正方法大致可分为基于优化的方法、灵敏度分析方法和特征结构分配方法。Jaishi[1]提出了基于多目标优化技术,利用特征值和残余应变能对有限元模型进行修正。Bell[2]利用无损测试数据,将多响应参数估计应用于结构的模型修正。Pavic[3]利用振动台,将灵敏度自动模型修正方法用于结构的有限元模型修正。这些模型修正方法已在简支梁、悬臂桁架等简单结构上得到验证。但是,对于大型复杂结构(如空间网架结构),由于有限元模型中存在大量的材料、几何特性及联结条件的不确定性,模型修正变得困难而复杂。
在空间网架中,节点形式多种多样,有近似铰接、近似完全刚接或是介于刚性连接和铰接之间的一种半刚性连接节点。但空间网架在计算过程中,通常是采用普通的空间铰接桁架理想化模型进行分析,因此铰节点的假设与空间网架中存在的实际节点条件明显地有所不同。在考虑半刚性节点的结构模型修正研究中,Law,Chan和Wu[4]提出了在模型修正中考虑半刚性节点的超单元,其半刚性节点的考虑主要是在单元刚度矩阵中引入弹簧刚度,由改进的求逆特征灵敏度方法修正结构的超单元模型。Terrell[5]等也考虑了节点的复杂性,利用约束的遗传子空间变换对结构有限元模型进行修正。
结构发生损伤后,会引起固有频率、振型、阻尼等模态参数发生变化,经过测试得到的振动信号包含有非平稳成分,因此经典小波变换、二代小波变换被广泛的应用于非平稳信号处理。其中同经典小波相比,二代小波变换是一种在时域内基于提升框架[6]构造小波的方法,不但计算速度快、计算方法简单,节省缓存空间,而且适于自适应、非线性和整数到整数的变换,具有极大的灵活性,非常易于实现。此外,运用提升小波分析还可以发现其它信号分析方法不能找到隐藏数据之中的表征结构特性的信息。因此,结构动力响应经提升小波包分解后得到的小波包分量能量虽然不是结构固有的动力特性参数,但小波包分量能量与模态频率和振型相比具有更好的损伤敏感性。DAVIS等[7]对多小波的提升方法进行了初步的研究,给出了多小波提升框架。为了有效地对结构进行健康监测,考虑模型的不确定性,可以将模糊系统与损伤特征向量相结合。Reda等[8]提出了在结构健康监测中基于模糊模式识别的损伤识别方法,其中智能健康监测系统的实现主要是利用模糊子集来提高模式分类。
本文提出了以提升小波包分量能量为特征向量,利用模糊模式识别理论对网架结构进行有限元模型修正的方法。首先建立半刚性节点固结系数表示的空间网架单元刚度矩阵,再对网架结构模型进行激振,得到结构的加速度响应信号,然后由基于提升框架的提升小波包变换对测得的信号进行分解,提取提升小波包分量能量建立特征向量,以此作为模糊模式识别的模糊子集,最后利用模糊模式识别方法对网架结构进行损伤识别,并研究了噪声对该算法的影响。数值模拟结果表明本文所采用的方法是可行的。
1 半刚性节点固结系数表示的空间网架单元刚度矩阵
建立空间网架结构单元的有限元模型,提出根据结构的节点抗转动刚度的变化来描述节点连接特性的变化,定义了节点固结系数来描述节点的连接特性[9,10]。

图1 端部半刚性连接梁单元模型Fig.1 Kinematics of a deformed beam element with semi-rigid connections
可以用图1来表示端部半刚性连接梁单元的有限元模型,其中弹簧用来模拟端部节点连接特性发生的变化。对于节点为刚接的结构,图中弹簧的抗转动刚度为无限大,即弹簧自身不发生转动;而对于节点为铰接的结构,弹簧自身将不能承受弯矩。因此,结构的节点连接特性的变化可以通过弹簧抗转动刚度的变化来表现。图中为梁左端转角,包括杆件自身弯曲引起转角及弹簧转动引起的转角为杆件自身弯曲引起的左端转角。由图1可知,弹簧转角φ=θ*-。定义节点抗转动刚度为:

式中,M1、M2分别为梁两端所承受的弯矩。分别定义梁两端的节点固结系数为:
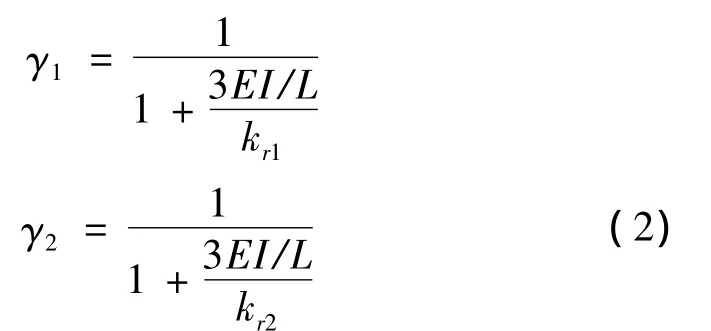
式中EI/L为梁的线刚度,节点固结系数与结构梁端节点的连接状态直接相关,可以用来表现结构中节点连接特性发生的变化。根据已有的试验研究可知,对于实际结构中的近似铰节点,0≤γ<0.143;对于半刚性连结节点,0.143≤γ<0.891;而对于近似刚性连结节点,0.891≤γ <1。
由本文中的数值算例结果表明,结构单元刚度矩阵中的扭矩对结构的动力特性影响很小。为了简化计算,忽略扭矩对结构单元刚度矩阵的影响,在单元刚度矩阵中扭矩项用零表示。因此,可以由以节点固结系数表示的平面框架结构单元的单元刚度矩阵,得到以节点固结系数表示的空间网架单元的单元刚度矩阵。

式中:f1=γ1+γ2+γ1γ2;f2=γ1(2+γ2);f3=3γ1;f4=3γ2;f5=3γ1γ2;f6=γ2(2+γ1);f7=4-γ1γ2。当 γ1=γ2=1时,式(3)即为以固结系数表示的空间网架结构梁单元的单元刚度矩阵。
节点固结系数的变化引起结构动力特性相应变化。所以,以节点固结系数表示的半刚性连结梁单元刚度矩阵可以有效的应用于结构有限元模型修正中。基于以上分析,利用半刚性连接梁单元的单元刚度矩阵公式,可以建立空间网架结构的有限元模型。
2 提升小波包分析
2.1 提升框架
提升框架方法是一种基于空间域的小波构造方法[11],通过提升框架改善小波特性构造出具有期望特性的小波基函数,成为构造第二代小波的基本工具。提升框架给出了双正交小波简单有效的构造方法,它通过使用多项式插值法来获得信号的高频分量,构建尺度函数获得信号的低频分量,主要包括分割、预测、更新三个步骤。
设原始信号序列为s={s(k),k∈Z},k=1,2,…,L,第二代小波变换的分解算法[11-12]为:
(1)分割:将原始信号序列分成偶样本序列{s(2k)}和奇样本序列{s(2k+1)}。
(2)预测:利用相邻的N个偶样本{s(2k)}预测奇样本{s(2k+1)},将预测误差d={d(k),k∈Z}定义为原始信号经过第二代小波分解后的细节信号(高频信号),即:
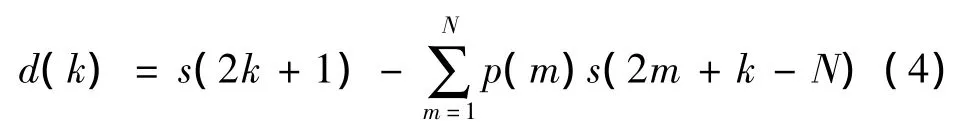
其中,P=[p(1),…,p(N)]T为N点预测器,p(m)为预测器系数,N为预测器系数的个数。
(3)更新:在获得细节信号{d(k)}的基础上,利用个细节信号更新偶样本{s(2k)},将更新后的信号序列s(k)定义为原始信号经过第二代小波分解后的逼近信号(低频信号),即:

其中:U=[u(1),…,u)]T为点更新器,u(m)为更新器系数,˜N为更新器系数的个数。
2.2 基于提升框架的小波包分量能量
利用基于提升框架的小波包分析对原始信号进行分解后[6],并对小波包分解系数进行重构,则第j层i个节点的能量为[13]:

其中是j层i个节点的重构信号。
由于结构出现损伤时,会对小波包分量能量有较大影响,因此可以以能量为元素构造特征向量T:

则特征向量T可以作为模糊模式识别的模糊子集,从而建立标准模糊集合进行结构的损伤识别。
3 模糊模式识别理论
模糊模式识别是把带有模糊特征的现象准确地归入某一类的过程。模式识别机制可以分为:设计与实现。设计是指用一定数量的已知样本进行分类器设计;实现是指用所设计的分类器对待识别的样本进行分类识别,即识别出与标准模式类相同或相似的对象。
模糊模式识别的方法[14]大致可分为最大隶属法(个体识别方法)、择近原则法(群体识别方法)、模糊聚类法等。本文主要利用模糊模式识别方法对结构进行有限元模型修正。
根据贴近度σ(A,B)作模式分类的择近原则:设论域为U,B∈F(U×U)为待识别对象,A1,A2,…,An∈F(U×U)为论域U中的n个已知的模糊子集,若 σ(Ai,B)=max{σ(Aj,B)|1≤j≤n},则认为B与Ai最贴近,判定B属于模式Ai。因此对实测的结构加速度响应信号作提升小波包分解,提取小波包分量能量作为模糊子集,利用择近原则以两向量的欧式距离最短作为识别标准,与标准模糊子集中的各模式进行目标识别,从而识别结构节点的固结系数,再代入结构单元刚度矩阵,实现修正结构有限元模型的目的。
4 数值算例
本文对一二层平板网架进行了有限元分析,该网架有13个节点,32根杆件。网架高0.6 m,长和宽都为4 m,杆的面积为 6.32E-4 m2,弹性模量为 2.07E11 GPa,剪切模量为8E10 GPa,密度为7 800 kg/m3。杆的惯性矩Ix与Iy为3.55E-7 m4,极惯性矩J为 7.1E-7 m4。网架结构见图2。

图2 空间平板网架Fig.2 The spatial truss structure
在网架结构的单元刚度矩阵中,选择网架结构单元刚度矩阵中不同的固结系数作为样本。由于结构的对称性,只考虑四类节点固结系数。为了获得网架结构的模拟加速度时程信号,选择结构节点2为输入激励点,进行白噪声激振,选择结构节点8为测点,分析中的时间步长均为0.04 s。
在测试中,不改变白噪声激振幅值的大小,采用Daubechies(DbN)系的小波Db1作为小波包基函数,对结构的单元刚度矩阵中的固结系数采用不同的值,计算得到结构的加速度信号,并对其进行三层提升小波包分析,提取提升小波包分量能量,共得到20组数据。以这20组数据归一化后作为训练样本,建立标准模糊子集,又从原测试样本中选取10组节点固结系数作为测试样本,见表1。同时,也利用经典小波包对测试信号进行小波包分解并提取小波包分量能量,测试结果表明,基于提升框架的小波包分解算法简单,运行速度快,计算速度大大高于经典小波包分解,因此在大型实际工程的结构在线健康监测中,利用提升小波包分析处理非平稳信号,可以有效地提高计算速度。

表1 10组不同节点固结系数的测试样本Tab.1 Ten test samples of different joint fixity factor
在无噪声的条件下,为了进行比较,分别利用按择近原则法的模糊模式识别方法和神经网络方法对固结系数进行了识别,识别结果见表2。

表2 节点固结系数的识别结果Tab.2 The identified result of joint fixity factor
从表2中可以看出,在无噪声的条件下,利用模糊模式识别方法和神经网络方法都可以对结构的有限元模型进行有效地修正。
为了比较噪声对该算法的影响,在这10组测试测试信号中分别加入5%、10%、15%和20%的高斯白噪声,其中对工况8(固结系数为 0.5、0.8、0.6 和 0.4)在不同噪声条件下,测得的结构8节点y方向加速度时程见图3。
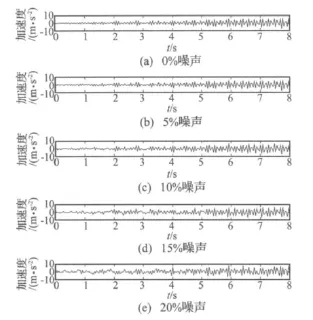
图3 第8组工况在不同噪声条件下的加速度图Fig.3 The acceleration time history of the eighth case based on the different noise
同样利用Db1小波,基于提升框架,对工况8的信号进行提升小波包分析得到的提升小波包分量能量见图4。
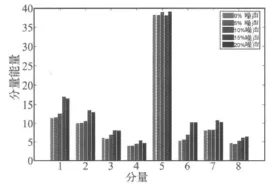
图4 不同噪声条件下的第8组工况的提升小波包分量能量Fig.4 The lifting wavelet packet component energy of the eighth case based on different noise
从图4中可以看出,随着噪声的增加,提升小波包分量能量大致呈上升的趋势。因此以这10组不同噪声条件下得到的提升小波包分量能量为测试子集,利用模糊模式识别和神经网络方法识别的结果分别见表3和表4。

表3 在不同噪声条件下,利用模糊模式识别理论识别的结果Tab.3 The identified result using fuzzy pattern recognition based on different noise
从表3中可以看出,利用模糊模式识别方法对固结系数识别过程中,在噪声不大于5%的时候,可以对固结系数进行准确的识别;当噪声为10%和15%时,识别的准确率差异较大,分别为80%和20%;而当噪声为20%时,已经不能对固结系数进行识别。
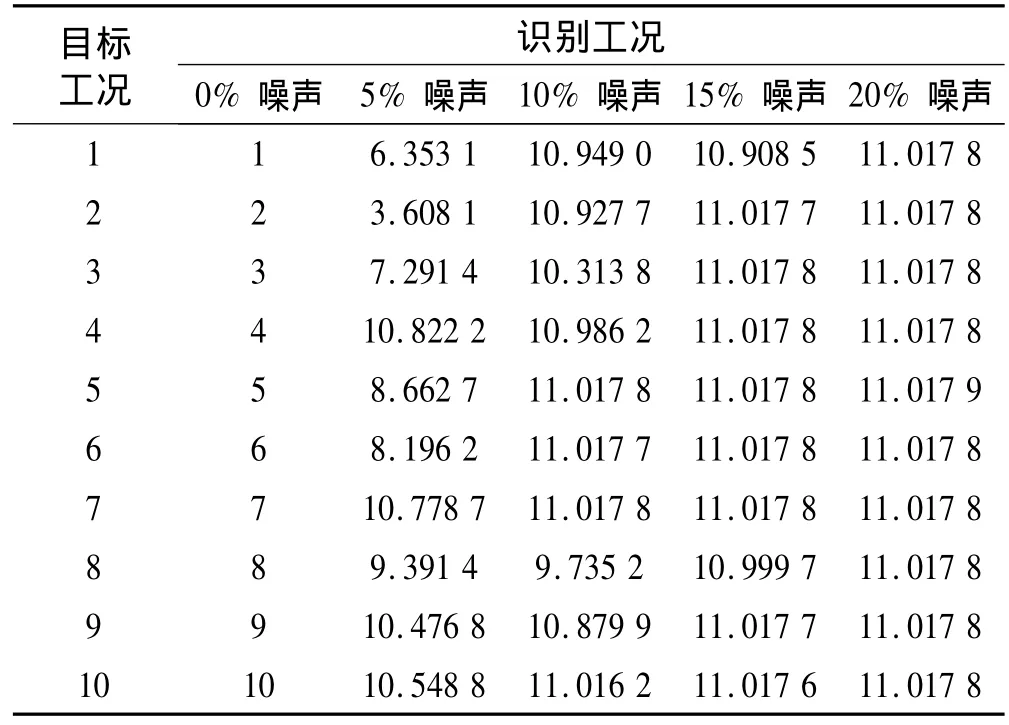
表4 在不同噪声条件下,利用神经网络理论识别的结果Tab.4 The identified result using neural net based on different noise
从表4中可以看出,由于神经网络用于非线性系统建模,存在模型结构确定困难、局部极小以及小样本下推广能力差,其测试能力与训练样本的选择有很大关系,利用神经网络方法对固结系数识别过程中,在无噪声条件下,可以对固结系数进行准确的识别;当噪声为5%、10%、15%和20%时,在小样本的条件下,已经不能对固结系数进行识别。
因此从表3和表4可以得到,在小样本的条件下,由于模糊模式识别很好地考虑了模型的不确定性,因此利用模糊模式识别理论可以对结构的节点固结系数进行有效的识别。
当测试数据不是原始数据时,另外取5组不同的固结系数,计算结构的加速度响应信号,然后用提升小波包分析得到提升小波包分量能量,作为模糊模式识别的测试子集进行识别的结果见表5。

表5 节点固结系数的识别结果Tab.5 The identified result of joint fixity factor
从表5的结果可知,由于标准模糊模式子集的数量较小,在小样本的条件下,利用模糊模式识别也可以对结构的固结系数进行粗略的识别。
由以上分析可以得出,提升小波包分析具有较好的抗噪声干扰能力,以提升小波包分量能量作为标准模糊子集的样本,可以在有噪声的情况下,有效地识别出结构的节点固结系数。将识别得到的节点固结系数代入以固结系数表示的结构单元刚度矩阵,再由坐标变换就可得到修正后的结构总的刚度矩阵,从而达到修正有限元刚度的目的。
5 结论
本文提出了基于提升小波包分析与模糊模式识别理论对网架结构进行有限元模型修正的方法。首先建立了半刚性节点固结系数表示的空间网架单元刚度矩阵,再对结构的振动测试信号进行提升小波包分解,提取提升小波包分量能量作为特征向量,建立标准模糊模式子集,然后利用基于择近原则法的模糊模式识别方法对网架结构进行有限元模型修正。为了验证该方法,对一个简化的网架结构模型进行了数值仿真,并研究了噪声对该方法的影响。研究结果表明,在小噪声的条件下,该方法能够有效地对网架结构进行有限元模型修正。
[1]Jaishi B,Ren W X.Finite element model updating based on eigenvalue and strain energy residuals using multiobjective optimization technique[J].Mechanical Systems and Signal Processing,2007,21(5):2295-2317.
[2]Bell E S,Sanayei M,Javdekar C N,et al.Multiresponse parameter estimation for finite-element model updating using nondestructive test data[J]. Journal of Structural Engineering,2007,133(8):1067-1079.
[3]Pavic A,Miskovic Z,Reynolds P.Modal testing and finiteelement model updating of a lively open-plan composite building floor[J].Journal of Structural Engineering,2007,133(4):550-558.
[4]Law S S,Chan T H T,Wu D.Super-element with semi-rigid joints in model updating[J].Journal of Sound and Vibration,2001,239(1):19-39.
[5] Terrell M J,Friswell M I,Lieven N A J.Constrained generic substructure transformations in finite element model updating[J].Journal of Sound and Vibration,2007,300(1-2):265-279.
[6]Sweldens W.The lifting scheme:a construction of second generation wavelets[J].SIAM Journal on Mathematical Analysis,1998,29(2):511-546.
[7]Davis G,Strela V,Turcajova R.Multiwavelet construction via the lifting scheme[C]. Wavelet analysis and multiresolution methods,Lecture Notes in Pure and Applied Mathematics,Marcel Dekker,1999:57-79.
[8]Reda Taha M M,Lucero J.Damageidentification for structural health monitoring using fuzzy pattern recognition[J].Engineering Structure,2005,27(12):1774-1783.
[9]陈 伟.应用神经网络技术的框架结构节点损伤诊断研究[D].武汉:武汉理工大学,2002.
[10] Yun C B,Yi J H,Bahng E Y.Joint damage assessment of framed structures using a neural networks technique[J].Engineering Structures,2001,23(5):425-435.
[11] Sweldens W. The lifting scheme:a custom-design construction of biorthogonal wavelets[J].Applied Computer Harmonic Analysis,1996,3:186-200.
[12] Cao H R,Chen X F,Zi Y Y,et al.End milling tool breakage detection using lifting scheme and Mahalanobis distance.[J].International Journal of Machine Tools &Manufacture ,2008,48:141-151.
[13] Pan Y N,Chen J,Li X L.Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means[J]. MechanicalSystems and Signal Processing,2010,24:559 – 566.
[14]瞿伟廉,郭佳凡,周 耀.高耸塔架结构节点损伤的一步诊断法[J].武汉理工大学学报,2005,27(12):65-67.

