天然河湾极限弯曲度

李志威，方春明

（中国水利水电科学研究院 泥沙研究所，北京 100048）

弯曲型河流是天然河流中最常见的一种河型，具有曲折迂回的几何形态和蜿蜒蠕动的动态特征。河湾是弯曲河流不可或缺的地貌组成单元，它的发展演变直接影响弯曲河流的河床演变和地貌过程。顺直河流是冲积河流暂时存在的不稳定形态［1］，通过水流泥沙运动与边界变化的相互作用，河流将从顺直变成微弯，经历长时间的凹岸冲刷和凸岸淤积后，最终变成弯曲河流。弯曲河流的河环发展到一定阶段，其弯曲度不断增大，河湾颈口变得狭窄而曲颈两端水位差较大，遇上洪水漫滩，很可能冲开颈口并形成新河，即发生自然裁弯。自然裁弯作为弯曲河流演变的一个拐点，可以大幅度地减少河湾的弯曲度，使之新河流又开始新的一轮演变，微弯，弯曲，高度弯曲直至自然裁弯。

弯曲度是表征天然河湾的弯曲程度最直观最重要的参数，一般将其定义为河道曲线长度与直线长度的比值。近20年以来，弯曲河流平面形态和分形特征成为国内外学者研究的热点问题，取得了一系列创新的成果。Snow［2］针对12条河流几何形态的分形几何研究得出，河道在一定尺度下表现分形特征，弯曲度与分形维数存在联系但这种关系不可直接测度，并认为分形弯曲度可以更全面反映河道几何特征。Nikora［3］利用已有的地图研究了摩尔达维亚河的46个河湾形态，认为河湾存在分形几何特征，得到了弯曲度与河床分形维数的关系。Howard［4］测量了33条弯曲河流的弯曲度、河湾波长、弯曲动量、河湾不对称性和不规则性，认为弯曲度是影响自由河湾形态变化最主要的4个参数之一。Andrle［5］认为传统测量河湾弯曲度方法随测量尺度、局部几何特征和分割步长变化，通过运用角度测量技术可以避免这些弊端，并可以更合理地测量河湾的弯曲度。Stolum［6］通过对自由弯曲河流模拟和经验数据解释了自然裁弯的发生和弯曲度的变化，并认为河湾演化是一种自组织过程，分形几何可描述河湾的临界状态，当河湾处在有序状态时，裁弯破坏这种有序；当河湾处在混沌状态时，裁弯产生新的有序，每个裁弯都通过局部形态变化，增加周围的其它裁弯发生的可能性。Montgom⁃ery［7］认为河湾弯曲度与分形维数之间存在显著相关且这种联系不受平面形态及环境变量影响，但两者之间也不存在成精确比例的关系。Gay［8］研究美国波德河的河湾，几十年的自然裁弯演变过程，研究表明当河湾的弯曲度达到极大时，只有发生大洪水，裁弯才可以发生和完成。Swamee［9］利用不同时期恒河的平面形态数据，研究得出控制恒河平面弯曲度的因素是地质构造、水沙条件、边界条件和新构造活动。Hooke［10］通过分析弯曲河流的弯曲度和河湾长度随时间变化关系，弯曲度随时间持续变大，只有在裁弯时弯曲度才会大幅减少。张斌［11］基于Google Earth卫星图像细致地研究了嘉陵江河湾的形态并与其它河湾形态对比分析，通过定义河湾的形态参数和测算，认为嘉陵江河湾是世界上最不规则和最弯曲的河湾之一。Constantine［12］运用Google EarthTM的卫星图像测算了30条弯曲河流的河湾和牛轭湖形态特征，研究表明弯曲度小于2.2的牛轭湖弯曲度与平均湖长成指数关系，建立了牛轭湖生成率与河道长度及弯曲度的表达式。白玉川［13］对黄河、长江和蓟运河的弯曲度几何分形分析认为，弯曲度掩盖了长河段的河湾发育的细节，不适于描述大型河流的弯曲性，分形维数较好地描述了大型河流的弯曲性和不规则性。

尽管前人对弯曲河流平面形态和弯曲度的研究已经取得较大进展，但弯曲度与河湾平面形态关系并不清晰，特别是河湾达到极大弯曲度或者即将发生自然裁弯时，河湾所能达到的极限弯曲度细节和内因始终没有得到揭示。以Google Earth为代表的卫星图像的易得性和可靠性，为广泛获得弯曲河流的平面形态数据提供了方便，从而为从统计学的角度研究河湾的极限度弯曲度提供了契机［12］。本文研究目的在于通过分析世界范围内弯曲河流的高弯曲度河湾，探索河湾在演变过程中在统计意义上是否存在一个极限弯曲度区间，正在裁弯或已经裁弯时的单个河湾弯曲度即可当作此时河湾的极限弯曲度。牛轭湖作为河湾达到极限弯曲度后，发生自然裁弯后遗留河段，它的弯曲度也具有参考价值。

1 研究方法

1.1 河湾参数定义河湾平面形态的定量参数是描述河湾几何外形的主要指标，选取河湾形态参数包括平均河宽B、曲颈宽度b、曲颈河宽Br、曲流颈长L、弯曲度S和河湾长度Lm（图1）。牛轭湖是河湾裁弯后的遗留河段，其形态参数定义相同。

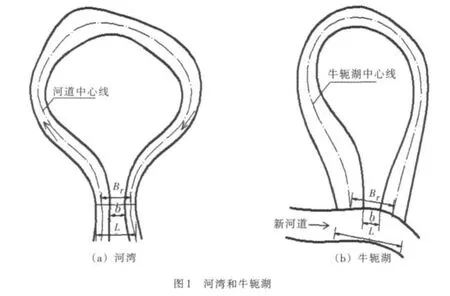
为了便于测算，定义单个河湾S为河湾长度与曲颈河宽的比值（Lm/Br），表示单个河湾的弯曲度，S越大表示河湾弯曲变形越强烈。SL为河湾的极限弯曲度，当河湾正裁弯或已裁弯时的弯曲度可以当作此时河湾的极限弯曲度。b/B为曲颈宽度与平均河宽之比，表示河湾发生自然裁弯的趋向性，b/B越小表示河湾越有可能发生裁弯。D为河湾的分形维数，它是河湾延展和弯曲的分形几何量度，可以描述其不规则性和复杂性。D值的计算不仅取决于河湾的平面形态，还与图形分辨率和计算方法有关。本文采用盒维数的方法计算河湾的分形维数，即采用不同的尺度去测算河道中心线的总河湾长度Lm，尺度越小，测算的曲线长度越接近河道的真实长度。

1.2 河湾选择本文旨在通过广泛选取高弯曲的河湾（包括正裁弯和已裁弯的河湾）和牛轭湖，测算其弯曲度，从统计意义上探究天然河湾是否存在极限弯曲度。前人研究认为［13］，随着河湾的凹岸侵蚀和凸岸淤积，河湾的曲颈将不断收窄，弯曲度也将增大，当河湾接近裁弯取直时，弯曲度趋向于无穷大。然而，自然裁弯均是由于周期性的汛期洪水漫滩，冲开河湾的曲颈造成的，具有不确定性。同时，按照单个河湾的弯曲度S为河湾长度与曲颈河宽的比值（Lm/Br）的定义，Br为河道中心线之间的距离，即使曲颈宽度b为0，Br也不会为0，因此弯曲度不可能趋向于无穷大。由此可知，河湾弯曲度不可能趋向于无穷大，只会达到某个极限值。

从严谨的科学研究来讲，必须长时间追踪众多河湾演变过程，最理想的情况是当这些河湾正发生自然裁弯时计算此时弯曲度，即为河湾的极限弯曲度。这种设想的实现难度和时间跨度均很难实现的，只有寻求以空间代时间，通过选取不同地域和不同河流的河湾，对不同发展阶段的高弯曲度河湾进行统计，才能知道到底河湾的极限弯曲度是否存在。根据这样的研究思路，作者统计了9条典型弯曲型河流（包括其支流）的共计128个河湾和111个牛轭湖（表1），作为探究天然河湾极限弯曲度的统计样本。未裁弯指河湾的弯曲度很大但尚未裁弯（图1）。正裁弯指河湾的颈口已经冲出一条较小流路，但旧河湾并未堵塞。已裁弯指河湾的新河已经形成，旧河湾的曲颈口开始部分堵塞。牛轭湖指新河流路已形成，旧河湾的颈口完全堵塞，遗留的旧河湾是一个封闭的水体（图1）。

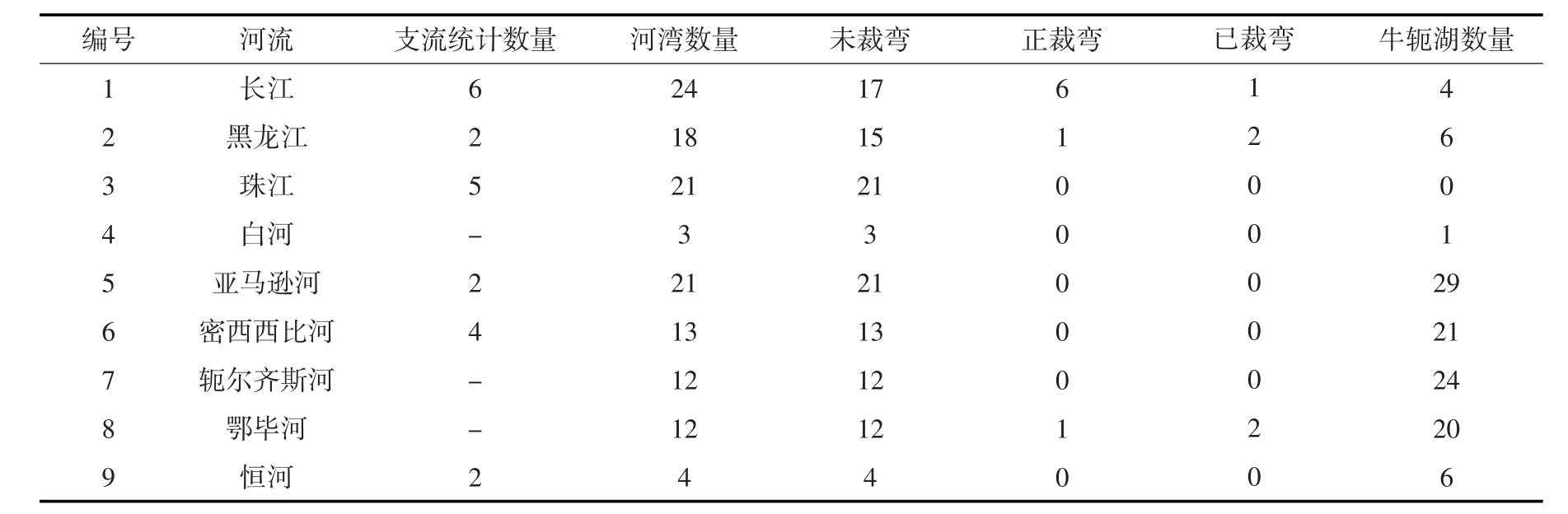
表1 河湾和牛轭湖统计

1.3 数据获取本文河湾数据来源于Google Earth卫星地图，Google Earth提供了全球范围任何地点的不同分辨率的卫星图像，用户可以通过调节识别高度来改变窗口可视范围和图像的分辨率。河湾选取是以弯曲度很大和图像清晰为准，而牛轭湖则侧重于可以辨识原河湾进口和出口痕迹为准，对远离现状河道的牛轭湖不予统计。将所有河湾和牛轭湖的图像插入AutoCAD界面，并对它们统一编号，以便复查和核对。通过Google Earth长度测量工具和CAD测量工具对比测量同一标准长度，从而确定光栅后图像的比例尺。利用CAD的绘图工具和测量工具相结合的方法测算河湾和牛轭湖的平面形态参数。河湾和牛轭湖的河道中心线绘制采用沿河段取中点连结成圆滑曲线，并运用图像处理软件Photoshop将所有河湾和牛轭湖的河道中心线图像，均以500×600像素保存为bmp格式。

由于所有测量均是在同一测量工具和相同方法下进行的，参数测量的相对误差是较小的。但受卫星图像分辨率和描图误差的影响，测算的参数值仍是近似的，实际上精确测量天然河湾的几何形态准确数值是非常困难的。本文测量数据与前人公布的数据相差较小，如本次测算长江中游的簰洲湾河湾的弯道长度55km，曲颈宽度为3.4km，与文献［14］给出簰洲湾的弯道长度约60km，曲颈宽度约4km，两组数据相差10%左右，造成差别的原因是与河湾进出口选取的位置有关。

2 河湾的极限弯曲度

天然河湾具有蜿蜒蠕动的动态机制，经历“微弯—强弯—裁弯”周期性的演变模式。河湾在发展过程中，弯曲度不断增大，在自然裁弯之前将达到这个河湾的极限弯曲度。对于单个河湾来说，所能达到的极限弯曲度是不确定的，与河湾所处的地质构造、水沙条件、边界条件和漫滩洪水等因素密切相关。但从统计学角度，对不同地域和不同河流的高弯度河湾的弯曲度进行测算与统计，可以得到在统计意义上，河湾所达到的极限弯曲度区间值。正在裁弯、已经裁弯的河湾及牛轭湖的弯曲度对河湾的极限弯曲度具有较高的参考价值。

2.1 极限弯曲度天然河湾趋近于极限弯曲度必须是正裁弯或已裁弯的河湾。本文统计了128个河湾和111个牛轭湖的弯曲度，河湾弯曲度变化区间为［3.4，30.2］，牛轭湖弯曲度变化区间在［3.0，27.5］，其中正裁弯和已裁弯的河湾在自然界数量较少，而高弯曲度河湾和牛轭湖却特别多。不管是未裁弯，还是正裁弯和已裁弯的河湾，其弯曲度并未达到特别大的值，更未趋于无限大（图2），这说明河湾弯曲度的上限值是存在的。根据本次统计的所有高弯曲度河湾来看，天然河湾极限弯曲度的上限值约为30，从正裁弯和已裁弯的河湾弯曲度来看，天然河湾极限弯曲度的下限值约为10（图2）。因此，从统计意义的角度可以初步确定极限弯曲度变化的范围是SL∈[ ]10，30，SL变化的幅度仍然很大，表明单个河湾的极限弯曲度是不确定的，取决于地质构造、水沙条件、边界条件和洪水漫滩等因素，但大量河湾的极限弯曲度却处在某一个区间。近50年以来，为了防洪安全和航运便利，国内外在大江大河上进行了一系列人工裁弯工程［15-17］。统计意义的极限弯曲度区间确立，可用来判断河湾在自然条件下发生自然裁弯的概率（图3），对高度弯曲河湾是否应该及时采取人工裁弯或人工护岸工程，具有一定的理论意义和实践价值。

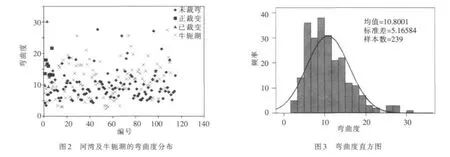
从统计样本来看，河湾和牛轭湖的弯曲度统计近似服从正态分布（图3），其中均值μ=10.8，标准方差σ=5.17。倘若河湾弯曲度大于极限弯曲度的下限值10时，可以认为此河湾发生自然裁弯的可能性极大，即随时有可能发生裁弯，这为是否实施人工护岸还是人工裁弯提供理论支持。如长江中游武汉市上游40km的簰洲湾的弯曲度已达到15［14］，大于极限弯曲度的下限，是否实施人工裁弯尚有激烈争议，但若不采取强固的人工护岸，在没有达到一致意见之前，突遇大洪水漫滩，簰洲湾也极可能发生自然裁弯。

2.2 极限弯曲度与河湾形态的关系河湾极限弯曲度既是河湾形态集中表现，也是是否发生裁弯的重要指标，而裁弯可以迅速改变河湾弯曲度，使之从强弯转向微弯。b/B为曲颈宽度与平均河宽之比，表示河湾发生自然裁弯的趋向性，若平均河宽远大于曲颈宽度，河湾在洪水漫滩时极可能发生自然裁弯。河湾和牛轭湖的弯曲度与b/B的统计数据呈“镰刀形”分布，具有较好规律性（图4）。当b/B值从小到大时，弯曲度先迅速变小，后基本维持在弯曲度等于3。弯曲度和b/B都在一定的变化幅度和趋向性，弯曲度越大，b/B值越小，反之亦然。正裁弯和已裁弯的b/B均较小而弯曲度较大。牛轭湖的b/B存在若干小值形成底部，这与牛轭湖进出口堵塞，分辨流路困难引起的测量误差有关。

河湾及牛轭湖的平均河宽表征了河道本身宽窄和横向拓展能力。弯曲度是河湾长度与曲颈河宽的比值，与平均河宽并没有直接关系。从图5可以得知，弯曲度与平均河宽的统计数据仍呈现较好规律性，当平均河宽从小到大时，弯曲度先迅速变小，变化到极小后又随平均河宽变大略有上升。正裁弯和已裁弯的平均河宽均较小，弯曲度较大，而未裁弯的平均河宽分布更为广泛。

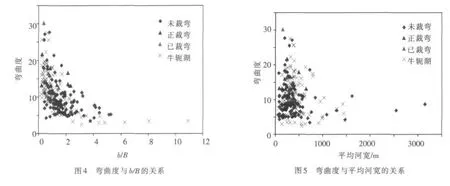
高弯曲河湾及牛轭湖的曲流颈长L表示河湾颈口的极大长度，也反映了河湾在裁弯前的收窄程度，与极限弯曲度是间接关系。弯曲度与L的样本统计数据呈现较好规律性，当样本L值从小到大时，弯曲度先迅速变小（图6），说明单个河湾演变时曲流颈长与弯曲度反向变化。正裁弯和已裁弯的L均较小，弯曲度较大，而未裁弯和牛轭湖的L值均广泛分布。

2.3 河湾的分形维数分形几何是以自然界描述不规则几何形态的几何学，分形理论已广泛应用于河流平面形态研究中，目前单个河湾以及复杂的河网形态具有分形特征已成为共识［2，3，7，17，18］。计算盒维数是一种简单且普遍使用的测定分形维数方法，本文采用计算盒维数的方法分析高度弯曲河湾和牛轭湖的分形特征，揭示分形维数用于表征河湾不规则性和复杂性的适用性，并从分析弯曲度与分形维数的关系。

当用边长为r方格测算河湾和牛轭湖的河道中心线时，可得到测量次数N。采用FractalFox软件调整r从8变化到800像素时（步长为1），可得到一系列（r，N），再用对数模型进行模拟，即可计算河湾的分形维数D值（图7），D=-lnN/lnr。从统计的河湾及牛轭湖的分形维数来看，D值主要集中在区间1.10～1.35之间，正裁弯和已裁弯的D值集中在1.25～1.35之间，而未裁弯和牛轭湖由于样本空间很大，故其D值的分布较为分散。经弯曲度样本的方差计算，分形维数D值的标准方差依次是正裁弯（s=0.026 5）、已裁弯（s=0.030 5）、未裁弯（s=0.052 7）和牛轭湖（s=0.055 0），这说明了统计样本越多造成的数据离散程度也越大。河湾处在正裁弯和已裁弯时，即达到极限弯曲度，弯曲度和分形维数的趋向一致。处在裁弯时的河湾形态，弯曲度极大其形态极不规则，分形维数表征了这一几何特征。然则，弯曲度量度河湾弯曲程度更为直观，计算简便，分形维数D值可作为弯曲度表征河湾几何形态的验证和补充。

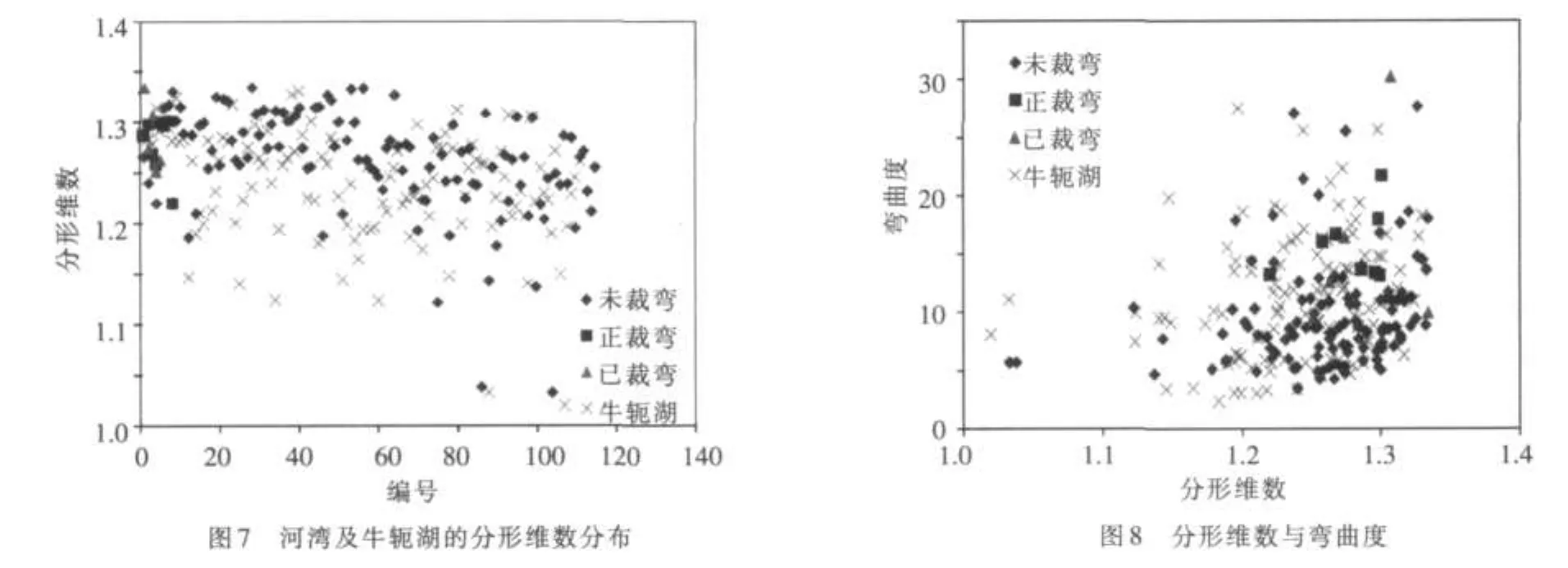
分形维数D和弯曲度S是两种描述河湾及牛轭湖的平面形态的指标，理论上分形维数D可以反几何形态的不规则性和复杂性。实际计算河湾及牛轭湖的分形维数D值时，D值越大说明河湾的变形越强烈，越不规则性，分形特征也越明显。分形维数D值主要集中于1.10～1.35之间，当分形维数D值增大时，弯曲度随之缓慢变大（图8）。正裁弯和已裁弯河湾的D值和S值均较大，说明两个形态参数表征河湾形态具有一致性。河湾的分形维数与弯曲度的这种一致性关系，与前人研究结果文献发现两者的紧密关系不谋而合［2，3，7］。

3 结论

（1）在统计意义上天然河湾存在极限弯曲度SL。根据河湾及牛轭湖弯曲度的统计和测算，河湾极限弯曲度的统计样本近似服从正态分布，初步确定河湾极限弯曲度变化范围SL∈［10，30］。极限弯曲度SL变化幅度仍然很大，表明单个河湾的极限弯曲度是不确定的，取决于地质构造、水沙条件、边界条件和洪水漫滩等因素。

（2）极限弯曲度统计区间的确立，可依据河湾的弯曲度来判断在自然条件下发生自然裁弯的可能性。对弯曲度大于极限弯曲度下限值10时，是否实施人工护岸和人工裁弯具有指导意义。

（3）弯曲度S和b/B的统计数据呈“镰刀形”分布，具有较好规律性。b/B≈2可看作河湾是否可能发生自然裁弯临界值。从统计样本来看，b/B、平均河宽B及曲流颈长L逐渐变小时，弯曲度S均先快速变小，到达极小值后逐渐趋于稳定。

（4）天然河湾平面形态具有分形特征，其分形维数D值主要集中于区间［1.10，1.35］。对正裁弯和已裁弯的河湾达到极限弯曲度时，分形维数D值也相应较大，D值表征了此时河湾的不规则性和复杂性。

（5）分形维数和弯曲度表征河湾几何形态具有一致性，当分形维数D值增大时，弯曲度随之缓慢变大。弯曲度表征河湾弯曲程度更为直观，计算简便，可作为判断河湾是否随时发生自然裁弯的定量指标，而分形维数只能作为河湾几何形态的可选测度，不能明确表征河湾几何形态和裁弯可能性。分形维数可作为弯曲度表征河湾平面几何形态的验证和补充，实际应用中以弯曲度为宜。

［1］倪晋仁，王随继.论顺直河流［J］.水利学报，2000（12）：14-21.

［2］Snow R S.Fractal sinuosity of stream channels［J］.Pure and Applied Geophysics，1989，131（1）：99-109.

［3］Nikora V.Fractal structures of river plan forms［J］.Water Resources Research，1991，27（6）：1327-1333.

［4］Howard A D，Hemberger A T.Multivariate characterization of meandering［J］.Geomorphology，1991（4）：161-186.

［5］Andrle R.Measuring channel planform of meandering rivers［J］.Physical Geography，1996，17（3）：270-281.

［6］Stolum H H.River meandering as a self-organization process［J］.Science，1996，271（22）：1710-1712.

［7］Montgomery K.Sinuosity and fractal dimension of meandering rivers［J］.Area，1996，28（4）：491-500.

［8］Gay G R，et al.Evolution of cutoffs across meander necks in Powder River，Montana，USA［J］.Earth Surface Process Science，1998，23（7）：651-662.

［9］Swamee P K，et al.Changes in channel pattern of river Ganga between Mustafabad and Rajmahal，Gangetic Plains since 18THcentury［J］.International Journal of Sediment Research，2003，18（3）：219-231.

［10］Hooke J M.Complexity，self-organization and variation in behavior in meandering rivers［J］.Geomorphology，2007，91（3）：236-258.

［11］张斌，艾南山，黄正文，等.中国嘉陵江河曲的形态与成因［J］.科学通报，2007，52（22）：2 671-2682.

［12］Constantine J A，Dune T.Meander cutoff and the controls on the production of oxbow lakes［J］.Geology，2008，36（1）：23-26.

［13］白玉川，黄涛，许栋.蜿蜒河流平面形态的几何分形及统计分析［J］.天津大学学报，2008，41（9）：1052-1056.

［14］殷瑞兰，车子刚，张细兵.簰洲湾演变机理及预测［J］.长江科学院院报，2002，19（5）：13-15.

［15］潘庆燊.下荆江人工裁弯30年［J］.人民长江，2001，32（5）：27-29.

［16］浦承松，温维超，杨树德.裁弯改直对南垒河孟连口岸段河床演变的影响［J］.泥沙研究，2004（4）：62-67.

［17］De Bartolo S G，Gabriele S，Gaudio R.Multifractal behavior of river networks［J］.Hydrology and Earth System Sciences，2000，4（1）：105-112.

［18］汪富泉，曹叔尤，丁晶.河流网络的分形与自组织及其物理机制［J］.水科学进展，2002，13（3）：368-366.