改进的EMD方法及大坝强震反应信号应用分析

许亮华，郭永刚，杜修力

（1.中国水利水电科学研究院 工程抗震研究中心，北京 100048；2.北京工业大学 建筑工程学院，北京 100124）

1 研究背景

HHT（Hilbert-Huang transform）信号分析方法［1-2］是Norden E.Huang在1998年提出的一种全新的数据处理方法，方法核心由两部分构成，即经验模式分解方法（EMD）和Hilbert变换。Hilbert变换得到的瞬时频率、振幅以及时频分布图等可以反应出数据的非平稳变化规律。虽然HHT方法在非平稳数据分析中得到广泛应用，但其方法本身仍然存在许多问题，如包络线拟合以及边界问题，没有确切公式理论支持，模态混淆等。这些问题需要得到解决才能推动HHT方法的进一步发展和应用。大坝强震反应信号是研究大坝结构特性的珍贵数据［3～5］，可以从中获得大坝的强震下非平稳反应规律、特性变化规律和损伤信息等有价值的信息，从而检验和改进大坝抗震设计，验证大坝抗震性能，保证大坝安全。大坝强震反应数据是一种非平稳数据，作者在应用HHT方法分析处理中发现，常规的EMD方法对频谱密集的数据分解不可避免产生模态混淆现象，导致HHT分析结果与实际偏差很大，分析结果无法作为结论进行应用。因此，应用HHT方法首先必须抑制模态混淆现象发生。

2 常规EMD方法

信号的EMD过程［1-2］是一个将非平稳信号进行平稳化处理的过程，分解目的是得到有近似窄带特征且尽量满足单分量函数［6］特征的固有模式函数（IMF），为下一步Hibert变换提供准备。

EMD过程是一个筛选获得IMF的过程，通过时间序列上下包络的平均值确定瞬时平衡位置，进而提取IMF。目前学者采用的EMD方法（为了与本文改进方法名称上区分，本文称之为常规EMD方法）步骤为：首先搜索查找出信号x（t）的局部极大值和极小值，利用三次样条曲线插值连接局部极大值和极小值点，分别得到极大值包络线和极小值包络线；其次对极大值包络线线和极小值包络线取平均，得到瞬时平均值m（t）；最后用原始数列x（t）减去瞬时平均值m（t），得到一个去掉低频的新数列 h（t）。

检查h（t）是否满足IMF的2个条件：（1）极值点数目和过零点数目相等或最多相差1个；（2）在任意点，上下包络线的平均值为0。

若h（t）满足上述两个条件，则将h（t）作为1个IMF；若不满足，将h（t）序列按照上述步骤进行重新“筛选”，直到满足下式

满足式（2）的两个条件就得到第1个IMF，记为c1（t）。

将c1（t）从原始数列中分离出来。将r1（t）作为新的信号重复上述步骤处理。经过处理后，原始数列x（t）依次被分解出n个IMF和一个残余项rn（t）其中残余项rn（t）代表了原始数列的趋势。

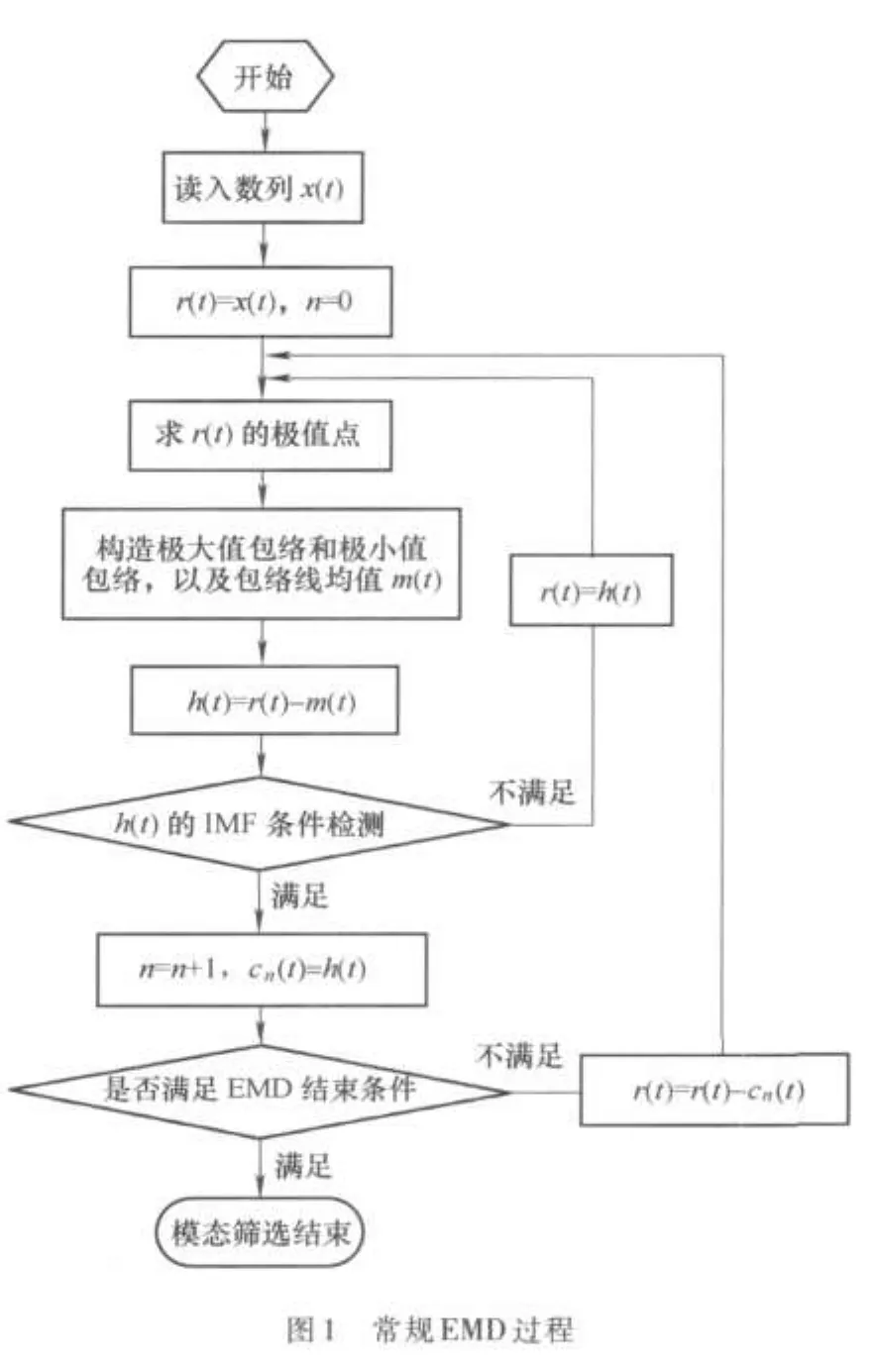
通过EMD分解得到的IMF在特点上非常适合作Hilbert变换，从而构造解析信号得到瞬时频率。以上是常规EMD分解过程，具体流程见图1。

3 基于滤波的EMD分解

在非平稳信号中，间歇信号、噪声信号和奇异信号存在，系统模态密集等因素会使EMD处理的IMF产生模态混淆，原因在于筛选得到的IMF并不能有效满足单分量函数特征。在提高信噪比，剔除奇异点，以及采取手段抑制端点效应的同时，如果信号保持窄带特性，那么EMD筛选得到的IMF必然保持窄带特性，这样可以尽可能避免模态混淆或降低模态混淆程度。为了解决常规EMD分解会产生模态混淆问题，研究人员将滤波处理和EMD方法结合起来，根据信号的傅立叶谱频带特征进行滤波处理，使得EMD分解时信号具有窄带特性。

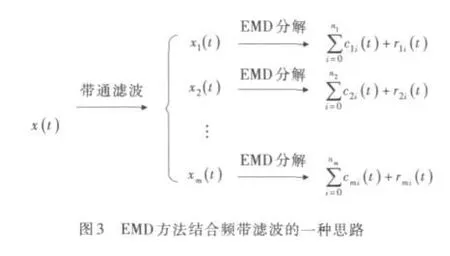
3.1 频带滤波与EMD方法结合应用其他学者的思路 许多方法普遍都是采取预滤波处理的思路（图3），对信号先行带通滤波［7-8］。首先将信号根据不同频带参数带通滤波获得几个带通子信号，对每个子信号分别进行EMD分解，筛选出各自的IMF；最后从所有带通信号的IMF中提取认为有用的IMF。

这种处理过程比较繁杂，生成了许多冗余IMF，失去了EMD方法的自适应性优势。这种处理思路对于批量数据的信号处理是不可行的。因为每个通道信号都要选择许多带通滤波的参数，再加上人为筛选判断IMF的过程，使求解效率大大降低，无法满足工程应用的要求。同时这样处理结果可能无法保证分解信号的完备性和正交性。这种滤波方法特点都是EMD前进行信号滤波，未触及EMD过程。

3.2 本文改进的EMD过程 基于前面滤波思路的不足，本文对于滤波思路进行改进，将滤波处理过程和EMD过程结合起来，在EMD分解的筛选过程中对信号进行滤波处理。通过改进，这种含滤波的EMD分解方法在保证了信号窄带特性同时发挥了EMD方法自适应分解的优点。

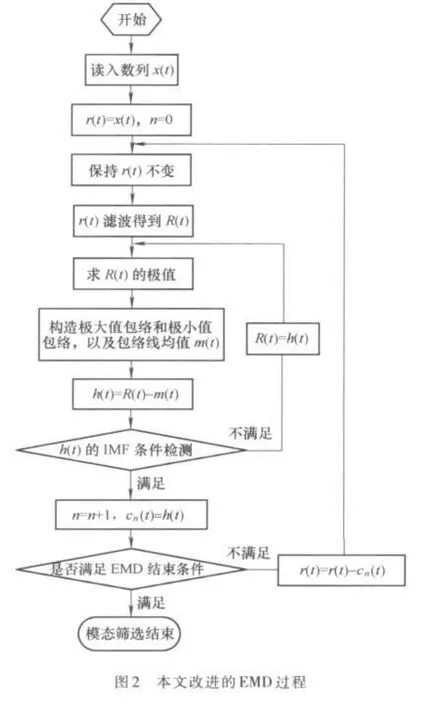
3.2.1 筛选流程的改进 首先对信号r（t）进行高通滤波获得R（t），将R（t）为EMD处理的信号，获取到一个IMF后，获取残余项时采用r（t）-c1（t）=r1（t）处理。将r1（t）项作为新的r（t）重复以上过程，直到满足筛选停止条件。改进的EMD流程见图2。

对于高频噪声较强且噪声频带分布较宽的信号，可以先进行低通滤波将信号噪声滤除提高信噪比后，再采用以上方法进行处理。

3.2.2 滤波参数设置过程信号r（t）高通滤波获得R（t）过程中滤波参数的设定可以采用以下两种方法设置。

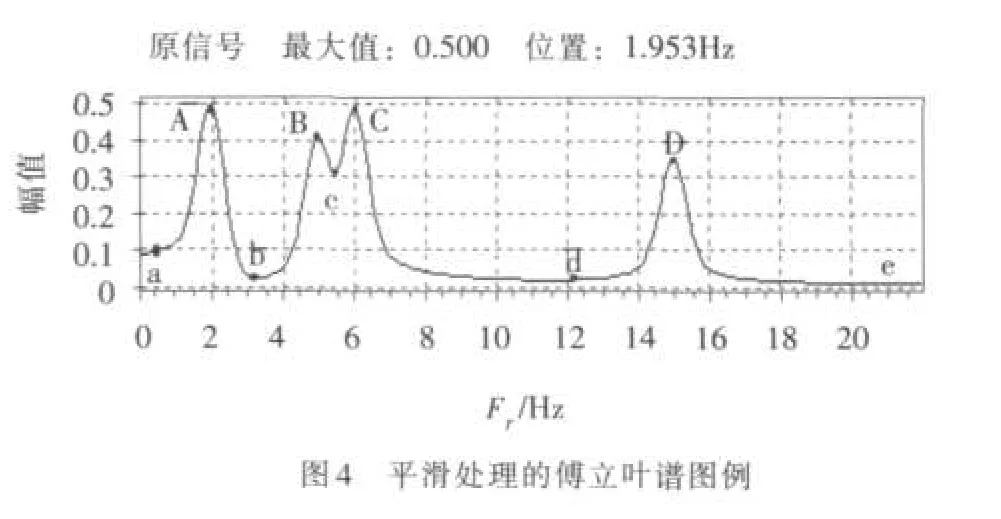
（1）自适应设置。这种方法的滤波参数是在EMD分解过程中自适应设置并滤波，不需要人为确定滤波参数。根据每次筛选进程中剩余成分r（t）的傅立叶谱，程序自行调整滤波参数。为便于描述，以一个仿真信号的傅立叶谱图（见图4）为例进行说明。过程为：①r（t）傅立叶变换，求出傅立叶谱；②傅立叶谱平滑处理，得到平滑后的傅立叶谱；③查找出傅立叶谱中一系列的局部极大值和极小值频率点，如例图4中所示的A、B、C和D共4个局部极大值和a、b、c、d和e共5个局部极小值；④找出局部极大值中频率最大的两个点C和D点，通过C、D两点确定出处两点间的极小值点d点。将d点的频率值作为本次高通滤波的最小频率参数；⑤对r（t）采用Fourier滤波器高通滤波得到R（t）。

对傅立叶谱平滑处理是为了便于查找极大值极小值，平滑程度要根据具体信号处理调节。如果信号是密集频率信号，谱平滑的次数要减少，否则，原本相邻的两个谱峰可能会合并成一个谱峰，滤波时便不能区分两个频带。

（2）预先设定滤波参数。信号频谱十分密集并且信噪比不高时，傅立叶谱平滑后划分的频带可能也不满足要求，EMD结果仍然有模态混淆现象，这时可以采用预先设定参数的方法。过程为：①对原始信号进行傅立叶分析，获得信号的傅立叶谱图。根据谱图特点先划分频带，获得每个频带的频率参数，按频率大小顺序依次设置滤波参数并保存；②在每次筛选IMF前，程序依次从设置的滤波参数中提取滤波参数对r（t）进行高通滤波。

4 实例分析

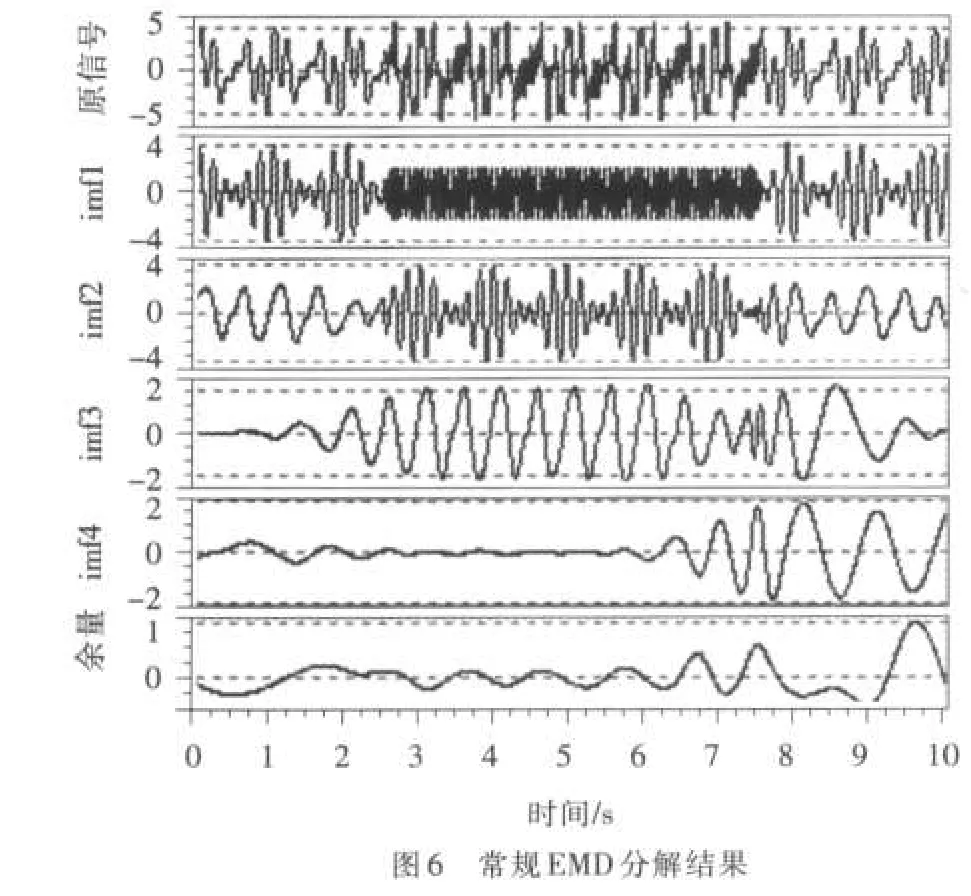
4.1 仿真信号分析 为讨论改进前后的分析效果，本文用最简单的简谐波构建仿真信号（见图5中No.1通道）。构成的各频率成分是15Hz的间歇简谐波及2、5和6Hz简谐波（分别见图5中No.2-5通道），构成的仿真信号含间歇信号具有密集模态的特点。

分别用常规EMD方法和本文改进的EMD方法对仿真信号进行分解。比较看出，常规EMD方法分解的imf1-4波形（见图6）与仿真信号成分No.2-5波形（见图5）明显不同，说明已经出现模态混淆。而本文改进的EMD方法分解得到的imf1-4（见图7），只是在端点处有轻微端点效应，间歇信号两端产生过渡信号。

对得到的EMD分解结果进一步进行Hilbert分析后，得到瞬时频率曲线。常规EMD方法得到的瞬时频率（见图8）波动大，特别是构成信号中5和6Hz简谐波的频率特征因为模态混淆，出现了错误的结果。而改进的EMD方法得到的瞬时频率（见图9），反应了正确的频率分布规律。这表明改进的EMD方法有效解决了模态混淆问题。

本文瞬时频率分布图中每个IMF的瞬时频率曲线的颜色深浅与相应的IMF瞬时幅值相关，瞬时幅值最大时瞬时频率用纯黑色表示，瞬时幅值等于0时瞬时频率用纯白色表现。

4.2 应用分析 目前在我国在水工建筑物特别是大坝上获得的强震动反应信号还不多，每个强震反应信号都是研究建筑物地震振动特征的珍贵资料。对于这些资料需要用各种方法，各个角度去分析应用，充分体现出这些数据的价值。

新丰江水电站［9］位于广东省河源县东江支流新丰江上，距广州市东北约160km。1962年3月19日库区发生了震级Ms为6.1级、震中烈度为8度的强烈地震。这次地震导致大坝右岸坝段头部108m高程出现长达82m的水平裂缝，地震后对大坝裂缝进行了修复加固。为了研究大坝断裂加固效果和裂缝上下两部分在地震作用下反应差异，设立了大坝裂缝研究台阵，以14、16、17号墩作为观测对象，在108m高程裂缝上、下各20cm布设拾振器。

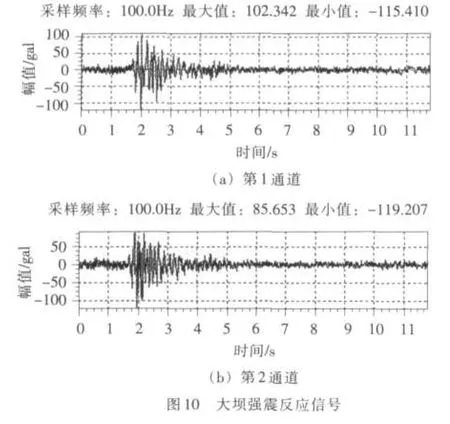
该大坝裂缝研究台阵，在1989年11月26日记录到震中距为2km的4.6级地震。本文提取这次地震中14坝段108m高程缝上和下、顺河向的强震反应信号（图10）进行HHT分析举例。

4.2.1 数据预处理 通过信号的傅立叶谱判断该大坝在此次地震中的卓越频率在10Hz以下，为了减少高频影响，对数据进行HHT处理之前先进行了10Hz以下的低通滤波，增加低频的信噪比，滤波后波形见图11。

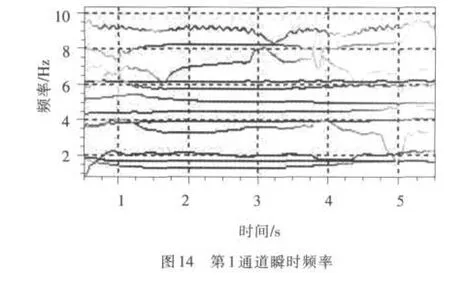
4.2.2 HHT分析 对预处理后的强震反应数据采用改进的EMD分解得到每个通道信号的IMF结果（见图12和图13），对分解结果进行Hilbert分析，计算得到各个IMF的瞬时频率和瞬时幅值，绘制得到瞬时频率分布（为观测强震阶段，1～5s作了放大，分别见图14和图15）和边际谱（见图16）。

EMD分解方法分解间歇信号时，由于分解是利用信号的包络，而包络对突变处的处理会导致分解的各个IMF结果在间歇信号开始和结束两个时间点处产生过渡信号。由IMF结果中的过渡信号获得的瞬时频率特征并非实际信息真实存在的瞬时频率，得到的瞬时频率在间歇信号两端会有较大的波动变化。结构强震反应信号在其非平稳性表现之一表现为各个频率成分振动幅值都增大过程和衰减过程，在幅值开始增大和幅值衰减到脉动水平时的两个时间点，相当于间歇信号的首尾两个时间点，得到的IMF结果同样会有过渡信号产生。研究瞬时频率变化必须针对每个频率成分的强震动阶段，在强震动阶段信噪比强，得到的瞬时频率才能够比较准确、接近实际值，从而反应出大坝结构强震动过程中的非平稳变化规律。

4.2.3 HHT分析结论

（1）通常由于放大效应影响，同一次地震中高程高的监测点监测信号的幅值要比高程低的相同方向的监测信号的幅值大。通过裂缝上下监测点强震信号的波形振动幅度大小可以看出，裂缝上的振幅却比裂缝下小（其它测点同样是这种规律），这表明修复的大坝裂缝具有一定的缓冲吸能作用。放大效应曲线在裂缝处会有所突变，并不是沿高程单纯放大。

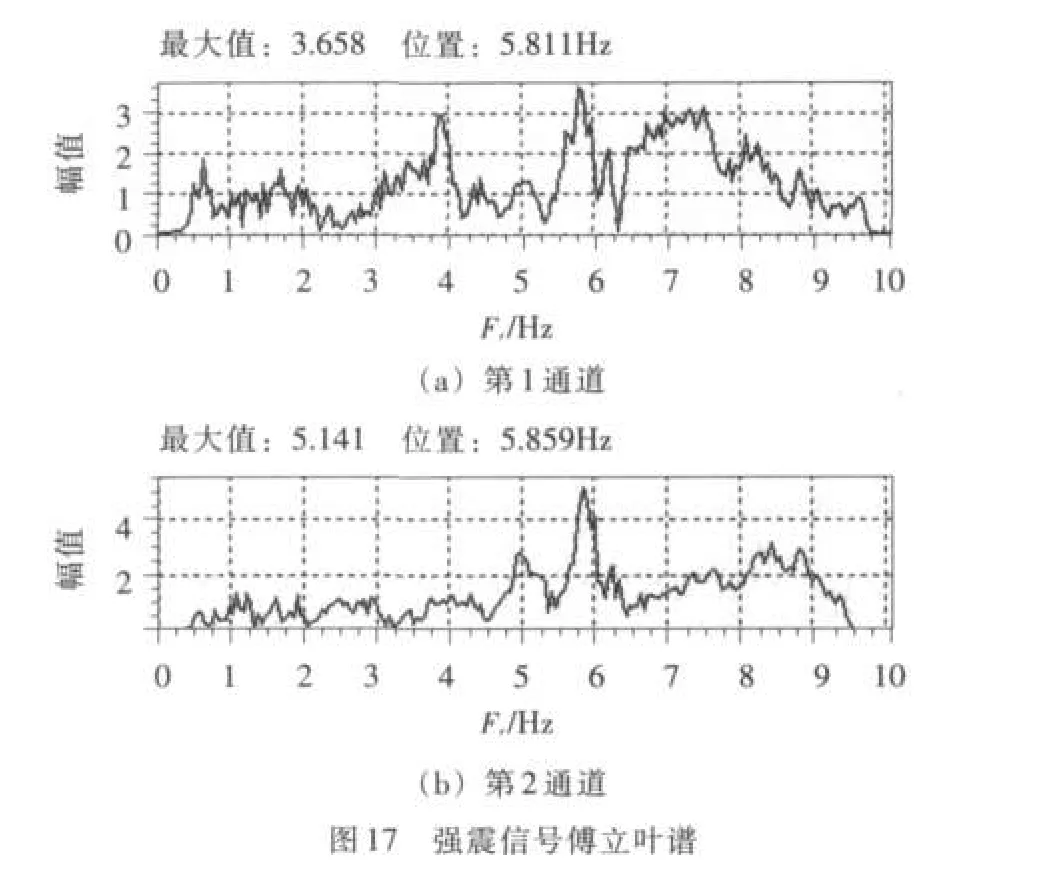
（2）大坝强震动的卓越频率。从傅立叶谱分析裂缝上下的卓越频率分别是5.811和5.859Hz。从边际谱分析本次强震的大坝卓越频率分别是5.762和5.859Hz。边际谱和傅立叶谱分别见图16、17。两种谱图的统计结果相近。频率分析结果与过去观测分析结果变化不大，这说明修复后大坝整体特性尚属稳定。

分析裂缝上下监测点强震信号的边际谱和傅立叶谱，发现各中心频率略有不同，表明裂缝对大坝震动的频率变化有一定影响。且各中心频率的谱幅值比值不成相似的比例关系，说明裂缝对不同频率的影响效果并不相同。具体裂缝对大坝振动的不同频率成分影响是否存在一定的规律有待继续深入研究。

（3）分别观察裂缝上下强震信号的瞬时频率分布图，可以看出裂缝上下强震信号各频率成分在强震阶段频率的瞬时频率曲线没有异常突变，基本处于水平波动变化，裂缝上下强震信号的各成分瞬时频率分布规律相似。这些表明大坝在这次强震中处于弹性振动状态，大坝修复后的裂缝在这次地震中处于安全状态。

5 结语

本文对常规的EMD分解过程进行改进，在EMD分解进程中采用滤波手段，这种改进方式可以有效抑制模态混淆。通过仿真数据和实际大坝强震数据的分析表明改进的EMD方法是有效可行的，可以用于大坝强震反应数据的分析处理中。

［1］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceeding of the Royal Society of Londom，1998，454：903-995.

［2］Huang N E，Shen Z，Long S R.A new view of nonlinear water waves：the Hilbert spectrum［J］.Annu.Rev.Flu⁃id Mech.，1999，31：417-557.

［3］DL/T5416-2009，水工建筑物强震动安全监测技术规范［S］.

［4］苏克忠，张力飞，等.大坝强震安全监测［M］.北京：中国水利水电出版社，1995.

［5］郭永刚.水利水电工程强震监测和强震监测仪器［J］.地球物理学进展，2005（2）：422-426.

［6］L.科恩.时—频分析：理论与应用［M］.白居宪译，西安：西安交通大学出版社，1998.

［7］Yangj N，Lei Ying，Pan Shu-wen，et al.System identification of linear structures based on Hilbert-Huang spec⁃tral analysis：part 1 normal modes［J］.Earthquake Engng Struct Dyn.，2003，32（9）：1443-1467.

［8］郭淑卿.EMD的频带滤波筛分方法［J］.中国民航大学学报，2008，26（4）：30-33，39.

［9］陈厚群，苏克忠，等.中国水工结构重要强震数据及分析［M］.北京：地震出版社，2000.