整星隔振平台的阻尼非线性对隔振性能影响的物理机理

张业伟， 方 勃， 李 松， 唐 冶， 王 龙

（哈尔滨工业大学 航天学院，哈尔滨 150001）

粘弹性阻尼隔振减振技术已广泛的应用在航空航天，汽车等领域的振动控制中，成为航空航天，汽车工程中不可缺少的关键技术。粘弹性阻尼器的隔振主要是利用粘弹性材料的剪切流动耗散能量特性来减小被隔振设备的振动［1－4］。

粘弹性阻尼材料的力学性能介于粘性和弹性之间，其本构关系复杂，建模困难，在大应变条件下表现出刚度非线性和阻尼非线性［5－7］。随着非线性振动理论和粘弹性理论的发展，分数导数本构关系能在较宽的频带内描述材料的力学行为等优点，逐渐的应用到描述粘弹性材料的本构关系，陈立群［8］利用分数导数粘弹性本构关系对弹簧－质量系统的简谐受迫振动进行了研究；闫启方［9］通过分数导数理论对阻尼隔振系统进行了研究。对于刚度和阻尼非线性模型有多种［10］，但国内外学者对于粘弹性阻尼材料的非线性研究多采用三次多项式函数和分数导数阶算子进行研究［11－13］。

本文结合实验现象，通过变形的立方多项式函数表示粘弹性阻尼器系统的刚度非线性，分数导数阶算子来描述隔振系统的粘弹性阻尼器阻尼特性，建立了整星隔振系统的非线性动力学模型，应用谐波平衡法得出从隔振器底端到卫星底端的振动传递率，利用简化等效动力学模型从物理机理上解释了实验现象，保证了航天器在发射过程中的安全性和可靠性。

1 实验现象

根据整星隔振平台设计的要求，课题组提出一种离型整星隔振平台，该隔振平台为嵌入式平台，与锥壳适配器串联，不改变卫星与运载火箭的接口。该隔振平台主要特点是能够满足多轴隔振的性能，结构简单，可靠性高，容易满足卫星发射要求。隔振平台的单个阻尼器是由粘弹性阻尼和两个夹板组成，其安装位置在锥壳与上圆环板连接处。为了考察整星隔振平台的振动特性，对整星隔振平台在振动台上进行了正弦扫频试验，测试所用的设备及系统如图1所示，试验平台如图2所示

图3为整星隔振平台在有8个阻尼器的工况下，在整星隔振平台底端分别输入1 m/s2（小幅值）和5 m/s2（大幅值）恒定加速度信号做为振动控制点，得到的从隔振平台底端到模拟卫星的振动传递率试验结果。

图3 具有8个阻尼器的振动传递率Fig.3 Vibration transmissibility of 8 Dampers

通过试验曲线（图3），可以看出对于含有8个阻尼器的隔振平台在大幅值激励下的振动传递率明显小于小幅值激励下的振动传递率。在小幅值和大幅值激励下，其一阶共振频率随着激励幅值的变化并未产生频率变化。

在相同工况下对具有8个阻尼器的离散型整星隔振平台进行了多次重复试验，其试验现象与上述一致，可见这种现象并不是由于测量误差的影响而产生的，并在同样工况下进行了含有4个阻尼器的试验，其试验结果如图4。

通过图4可以看出具有4个阻尼器的隔振平台所产生的试验现象与具有8个阻尼器的隔振平台试验现象一致。

图4 具有4个阻尼器的振动传递率Fig.4 Vibration transmissibility of 4 Dampers

2 具有粘弹性阻尼器非线性的整星隔振系统动力学模型

分析上述实验现象可能是由于整星隔振平台试验采用的是正弦扫频试验，在正弦扫频试验中，总的激励量级高，粘弹性阻尼器系统非线性阻尼的效果被强烈激发出来，从而粘弹性阻尼器系统的阻尼非线性引起整星隔振系统的振动传递率发生变化，离散型整星隔振平台表现出不同的隔振性能，下面从物理机理上进行了下述理论分析。

10月23日《检察日报》有篇文章，叫《认为“也许没事”，结果越陷越深》，说的是一个贪官的“忏悔”。我记得，该报曾刊过一篇类似“也许没事”的文章，标题忘记，我读了，对那贪官可笑的说辞，颇不以为然，写了篇短评予以“冷嘲热讽”，于谈笑间轻轻一刺，因为对此实在没有多少道理可讲。未曾想到，三四年过去，又有落马贪官，臊眉耷眼地拿“也许没事”的老调重弹了——荒诞如此，令我不由连声哀叹。

根据文献［14］整星隔振系统简化等效动力学模型的方法，建立能够反应整星隔振系统一阶振动特性的含有粘弹性阻尼和刚度非线性阻尼器的整星隔振系统简化等效动力学模型，如图5所示。

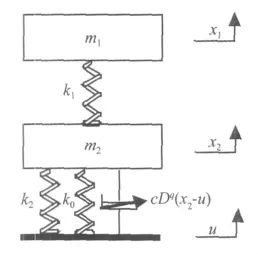
图5 动力学模型Fig.5 Dynamic model

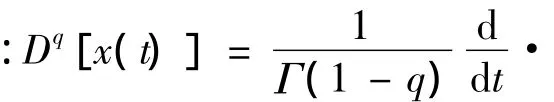
因此，整星隔振系统的振动方程为：

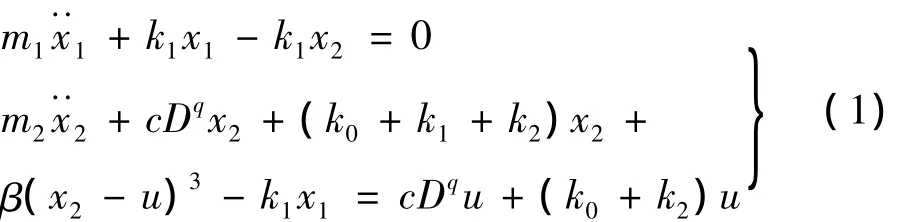
同时引入变量 y1=x1－ x2，y2=x2－ u，c/m2=2ξp2，k1/m1=p21，（k2+k0）/m2=p22，m1/m2= γ，η = β/（k0+k2），然后代入（1）进行无量纲化处理。

则系统的振动方程（1）化为：

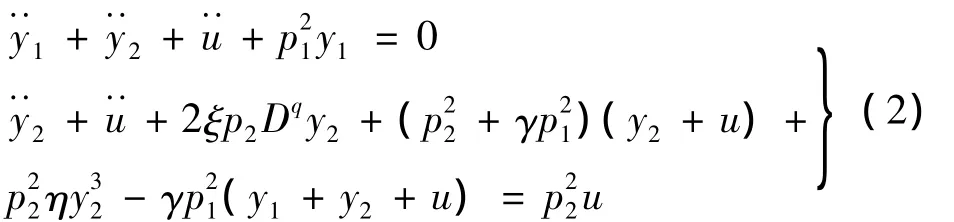
下面用谐波平衡法的近似稳态周期解，求出系统的频率响应方程。设其稳态谐波一次近似解为：

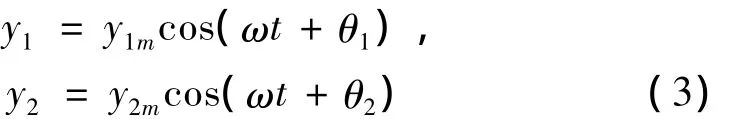
将公式（3）代入公式（2），令一次谐波系数分别相等（忽略高次项），这样得到4个方程，即：

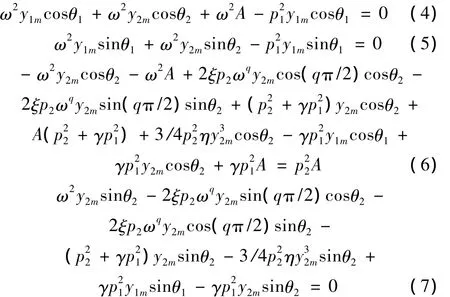
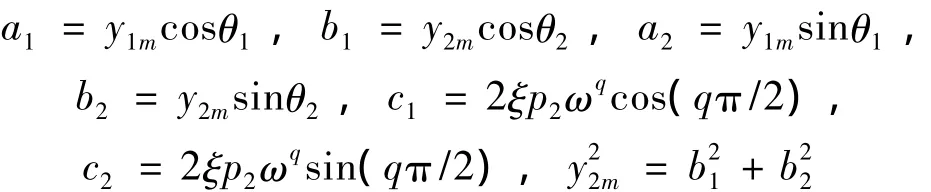
代入方程（4）、方程（5）、方程（6）、方程（7）可以得到：

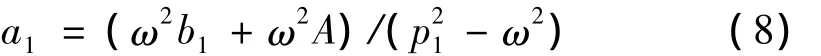
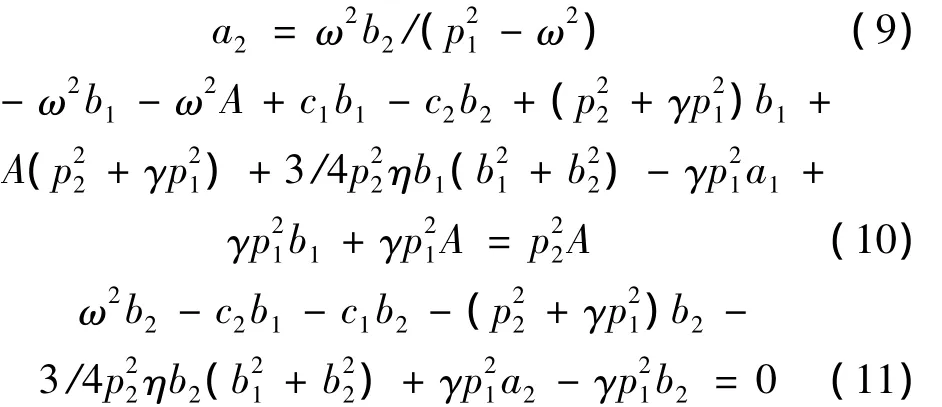
利用式（10）、式（11）的数值解可以得到b1、b2，然后根据式（8）、式（9）解得 a1、a2、，从而可以求得 x1的稳态周期解，其表达式为：

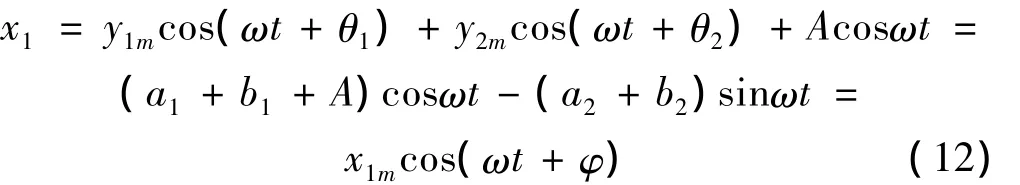
因此，从隔振器底端到卫星的位移振动传递率：

由于试验中采用的输入信号为加速度响应信号，所以激励幅值表达式

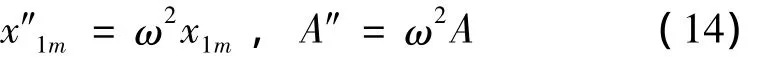
则可知：

3 数值分析

为了从物理机理上对实验现象进行解释，下面对整星隔振平台动力学模型进行了数值研究，分析当隔振平台的激励幅值变化、粘弹性阻尼器系统的刚度非线性变化，阻尼非线性变化时系统的振动传递率变化规律。

首先分析当隔振平台的激励幅值A″=1 m/s2；A″=5 m/s2时从隔振平台底端到卫星的振动传递率变化规律，当隔振平台的激励具有小幅值和大幅值时，根据式（13）数值仿真得到系统的一阶振动传递率曲线，这时q=0.7，β/（k0+k2）= －0.2，其仿真结果如图 6所示。

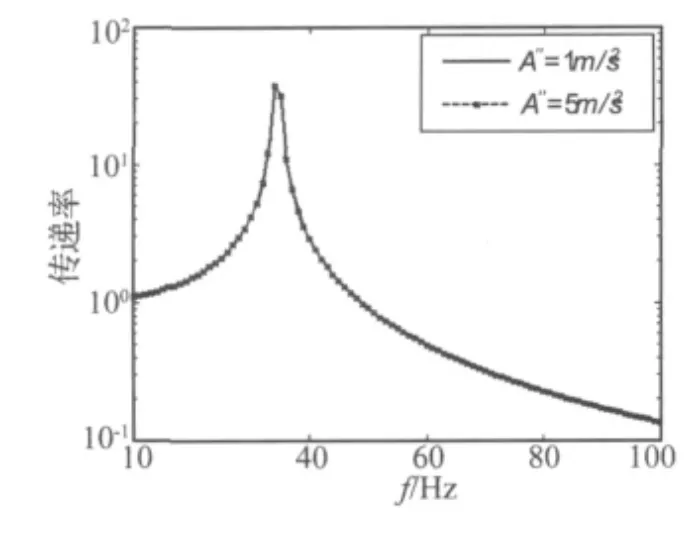
图6 不同激励幅值时振动传递率对比Fig.6 Contrast of vibration transmissibility under different excitation amplitudes

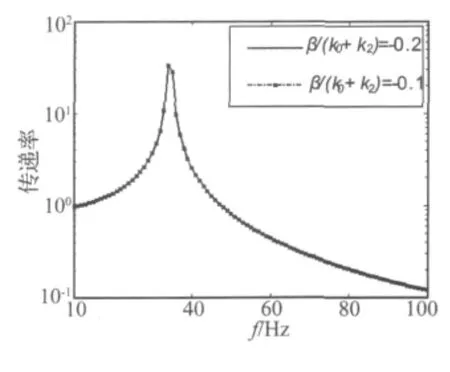
图7 非线性刚度项不同时振动传递率对比Fig.7 Contrast of vibration transmissibility under different nonlinear stiffnesses

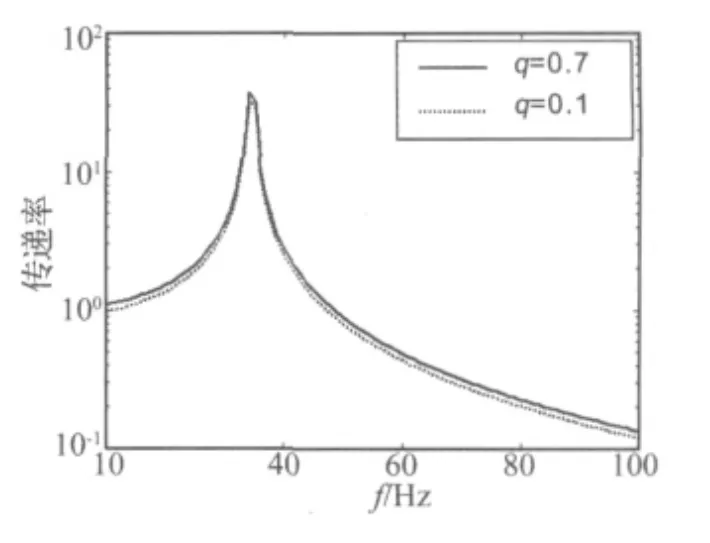
图8 非线性阻尼项不同时振动传递率对比Fig.8 Contrast of vibration transmissibility under different nonlinear dampings

从图6中看出，在小幅值和大幅值激励下，虽然系统的共振频率未发生变化，但是从隔振器底端到卫星的振动传递率曲线几乎吻合。综上所述，激励幅值的变化并不能引起系统振动传递率变化。

下面讨论在不同激励幅值下，当粘弹性阻尼器系统的非线性刚度变化时系统的振动传递率变化规律，令A″=1 m/s2，β/（k0+k2）= －0.2；A″=5 m/s2，β/（k0+k2）=－0.1；系统的参数q=0.1且k0+k2保持不变，讨论体现粘弹性阻尼器系统的非线性刚度项β的变化对系统的振动传递率影响，其仿真结果如图7所示。

从图7中看出，在小幅值下和大幅值激励下，非线性刚度项β的变化也并未引起系统的振动传递率发生变化。

下面讨论在不同激励幅值下，体现粘弹性阻尼器系统的阻尼非线性q变化时，系统的振动传递率变化规律，令q=0.7，A'=1 m/s2，β/（k0+k2）= － 0.2；q=0.1，A'=5 m/s2，β/（k0+k2）= －0.2。

从图8中看出，在大幅值下从隔振器底端到卫星的振动传递率相对于小幅值时振动传递率减小，且系统的共振频率未发生变化，该现象与试验分析所得到的现象一致，由此可见在大激励幅值工况下粘弹性阻尼系统的阻尼非线性被激发出来，从而，粘弹性阻尼系统阻尼非线性的变化引起系统振动传递率的变化。从物理机理上解释了粘弹性阻尼器的阻尼非线性是引起在不同幅值下的振动传递率变化的根本原因，隔振器表现出不同的隔振性能，并且可以看出当运载火箭对隔振平台的激励是变化时，离散型整星隔振平台的共振频率未发生漂移，不会与运载火箭的共振频率发生耦合。

4 结论

离散型整星隔振平台能够大幅度改善卫星的发射环境，但是为了保证卫星发射的安全性和可靠性，需要对隔振平台在应用中出现的现象进行研究，并为其他整星隔振器设计和试验提供参考。在离散型整星隔振系统试验中发现，随着激励幅值的增加系统的振动传递率减小，一阶共振频率未发生变化，针对该现象本文从物理意义出发建立了整星隔振系统的一阶等效非线性动力学模型，利用数值解针对此现象进行了研究，给出了一种物理机理解释，发现整星隔振系统的激励幅值变化能够引起粘弹性阻尼器系统的阻尼产生非线性现象，该现象是引起系统振动传递率变化的根本原因，因此在隔振平台的设计中应结合整星隔振系统的实际环境，合理的设计粘弹性阻尼器，并在考察隔振平台的隔振性能试验中，应使用较小幅值的正弦扫频试验，这更适合评价整星隔振平台的隔振效果。

［1］Borden M，Dugundji J.Joint damping and nonlinearity indynamics of space structure［J］.AIAA of Journal，1990，28：740－749.

［2］范蓉平，孟 光，贺才春，等.粘弹性阻尼材料降低列车车内噪声的试验研究［J］.振动与冲击，2008，27（6）：123－127.

［3］ Du H J，Zou Z Z，Huang W H.Vibration suppression analysis for supporter with constrained layer damping［J］.Journal of Harbin Institute of Technology，2004，（2）：231－236.

［4］陈 阳，方 勃，曲秀全，等.新型整星隔振器隔振性能分析［J］.宇航学报，2007，28（4）：986 －989.

［5］Gement A.On fractionaldifferences［J］.Philosophical Magazine，1938，25（1）：92 －96.

［6］黄文虎，王心清，张景绘，等.航天柔性结构振动控制的若干进展［J］.力学进展，1997，27（1）：5－18

［7］Lesieufre G A，Bianchinie E.Time domain modeling of linear viscoelaticity using anelastic displacement fields［J］.Journal of Vibration and Acoustics，1995，117（4）：424 －430.

［8］陈立群.一类质量—黏弹性弹簧系统的简谐受迫振动［J］.力学与实践，2001，23（5）：49 －51.

［9］闫启方，刘林超，陈 哲.分数算子描述的两级粘弹性阻尼隔振系统的幅频特性分析［J］.噪声与振动控制，2006，26（2）：7－10.

［10］付兰芳，张 宪，安 居，等.非线性振冲隔离器油阻尼特性模型及参数识别［J］.振动与冲击，2010，29（5）：133－135.

［11］ Bagley R L，Torvik P J. Fractional calculus adifferent approach to the analysis of viscoelastically damped structures［J］.AIAA of Journal，1983，21（5）：741 －748.

［12］陈安华，刘德顺，朱萍玉.被动隔振体的非线性振动分析［J］.机械工程学报，2001，37（6）：99 －105.

［13］周 超，吴庆鸣，张 强，等.粘弹性阻尼隔振体的非线性振动分析［J］.工程设计学报，2009，16（3）：205

［14］ Liu L K，Zheng G T.Parameter analysis of PAF for wholespacecraft vibration isolation［J］.Aerospace Science and Technology，2007，11：464 －472.

［15］ Zhang W. Nobuyukishmizu. Damping properities of viscoelastic material described by fractional kelvin-voigt model［J］.JSME Intenational Journal Series C，1999，42（1）.

［16］ Kenneth S M.An introduction to the fractional calculus and fractionaldifferentialequations［M］.New York John Wiley＆Sons Inc，1993.