差分振子相图的自动识别与应用

胥永刚， 马海龙， 冯明时， 崔玲丽

（北京工业大学 机电学院 北京市先进制造技术重点实验室，北京 100124）

差分振子用于微弱信号检测，可以实现机电设备故障的早期检测。与混沌振子、随机共振等非线性方法相比，差分振子不需要解微分方程，运算速度快，适用于实时监测，是一种可视化的微弱信号的检测方法。差分振子对微弱信号的检测是将待检测信号输入差分振子后，通过振子相图的变化来判断信号中是否含有待检测的频率。这一判断到目前为止都是通过人的感官来判别，不利于自动化检测的实现，且在噪声较大的情况下，有可能出现误判。常用的图像的识别方法如Hu 氏不变矩［1］、仿射矩［2］、Zernike 矩［3－6］等方法，已经被应用于轴心轨迹、混沌振子相图和图形的识别中，并取得了很好的效果。但是将以上方法用于差分振子的相图轨迹识别中，实验结果表明：这些方法不能够有效地识别不同状态下的相图。不同的差分振子相同出现了相近的矩值，而且矩的值也不呈现规律性。根据差分振子相图的特点，给出了一种新的方法对差分振子的相图变化进行识别。

1 差分振子的基本原理

差分振子是以差分方程为基础构造检测器，其数学模型如下：

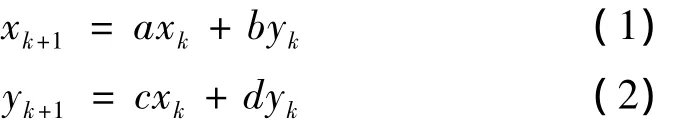
令：α=－（a+b）β=ad－bc

利用消元法，消去变量yk，得到一元差分方程如下：

当α、β满足以下条件：

系统的固有频率ω0可以通过下式进行估计：

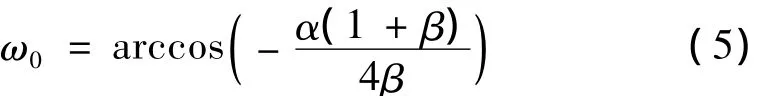
以差分方程为基础的差分振子检测器构造如下：

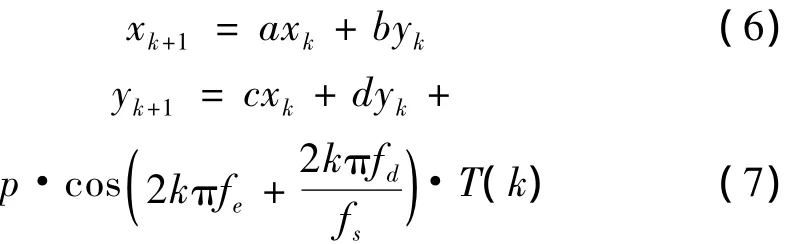
其中：p是放大倍数，fe是系统激励频率，T（k）是检测信号，fd是检测频率，fs是采样频率。

适当地调节检测器的各个参数就能达到对信号频率的识别，即：若差分振子图像收敛于极点，则信号中不含有待检测频率；若差分振子图像收敛于极环，则信号中含有待检测频率［7，8］。下面通过对一个仿真信号进行检测来说明差分振子的有效性，构造一个仿真信号如下：

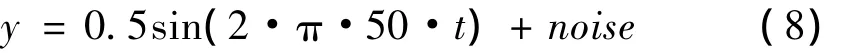
其中：noise是随机噪声，采样频率：fs=1 000 Hz，采样点数：N=8 192；利用差分振子分别检测50 Hz和55 Hz的频率成分。因信号中含有50 Hz这一频率，所以检测50 Hz（即fd=50）频率成分时，差分振子相图应收敛于极环状态，而检测55 Hz（fd=55）频率成分时，因信号中不含有这一频率，所以差分振子相图收敛于极点。差分振子的其它参数设置如下：α=0.95，β=0.99，激励频率fe=0.329 2，放大倍数p=1。检测结果如图1所示。

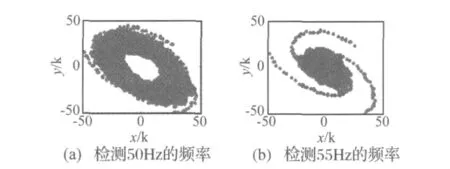
图1 差分振子检测信号的振子相图Fig.1 Differential resonator phase diagran of detected signal

2 差分振子相图的识别

对差分振子的相图进行识别就是要对差分振子的相图状态进行识别，即对信号中是否存在待检测频率进行自动判断。若信号中含有待检测频率，则对该频率成分幅值的大小进行定性的判断。对差分振子的相图状态进行研究，找出检测频率幅值大小与差分振子相图的关系。

2.1 检测频率的幅值对差分振子相图的影响

差分振子的参数对差分振子的相图影响很大，即使同一信号，输入差分振子后，在不同的参数下表现出的极环的状态是不相同的。因此不同参数下的差分振子相图是无法比较待检测信号频率幅值的相对大小，其比较也是无任何意义的。在相同的参数条件下，差分振子相图的变化能够反映出待检测频率幅值的变化，通过差分振子相图的变化判别待检测频率幅值的相对大小。下面通过仿真信号来说明待检测频率幅值与差分振子相图的关系。构造仿真信号如下：

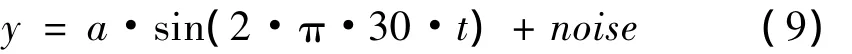
其中：待检测信号频率30 Hz，noise是随机噪声。采样点数N=8 192，采样频率fs=1 000，a是信号中30 Hz频率成分的幅值。改变a的值，观察差分振子的相图变化情况。差分振子的参数如下：α=0.95，β=0.99，放大倍数p=2.5，激励频率fe=0.329 2，检测频率fd=30。不同幅值下的差分振子相图如图2所示。

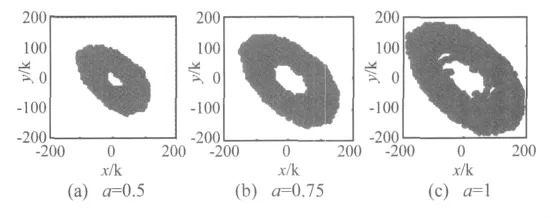
图2 不同幅值下的差分振子图像Fig.2 Differential resonator phase figure with different amplitudes

从图2中可以看出，a=0.5时差分振子相图所占的区域为100×100，a=0.75时，差分振子相图所占区域为150×150，a=1时差分振子相图所占区域为200×200。可见随着a的增加，差分振子相图的极环所占区域也近似地按照相应的比例增大。在差分振子参数相同的条件下，差分振子极环的大小反映了待检测频率幅值的大小，极环越大，相应的待检测频率的幅值越大；差分振子收敛的极环间的倍数关系与待检测频率幅值间的倍数关系近似相等。

2.2 差分振子相图的识别

在实际应用过程中，可识别的差分振子的相图主要有如图3所示三种形态。

图3中（a）表征信号中不存在待检测频率，（c）表征的是信号中存在待检测频率。而（b）则是介于（a）和（c）中间的一种形态。由2.1节中可知，（b）表征存在待检测频率，但是待检测频率的幅值相对较小。可以看出，差分振子相图收敛于极点与收敛于极环的最大区别就是，振子的输出是否在相图的坐标原点大量地聚集。

针对差分振子相图的特点给出以下判别准则：

（1）将差分振子的相图归一化即振子相图的横纵坐标均在［－1 1］内。

图3 差分振子相图的三种形态Fig.3 Three states of differential resonator phase diagram

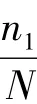
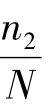
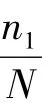
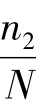
下面应用以上的判别准则对图3中的差分振子相图进行判别。经计算图3（a）中：n1/N=0.255 4显然大于0.1收敛于极点。图3（b）中n1/N=0.002 9小于0.02，收敛于极环。图3（c）中n1/N=0收敛于极环。可见通过以上准则就可以判断差分振子相图的状态。

研究和实验表明，n1/N或n2/N的值越小，说明在中心区域点的密度越小，即收敛于极环的程度越大，相对应的待检测频率的幅值也就越大。因此图3中（c）的待检测频率幅值要大于（b）中待检测频率的幅值，与前述结论一致。对于同样收敛于极环的两个信号的差分振子相图来说，n1/N（或n2/N）小者其对应的待检测频率的幅值要大一些。

若差分振子的参数调节不适当，差分振子相图会出现各种“畸形”，如图4所示。这些畸形的相图使得差分振子的相图的状态难以判断，如图4，这些差分振子相图是无法识别其是收敛于极点还是收敛于极环。

图4 差分振子“畸形”相图Fig.4 Deformity of differential resonator phase diagram

由于“畸形”相图的存在导致对于振子相图的无法识别或者是识别错误，因此对于差分振子参数的调节是决定差分振子相图识别成败的关键所在。对于差分振子相图的识别是建立在相图的非“畸形”的基础之上的，否则其识别是无意义的。

3 实验验证

实验系统由轴承故障模拟实验台、笔记本电脑和HG3604故障诊断仪组成。轴承故障模拟实验台如图5所示，由两个6 307深沟球滚动轴承支撑，通过挠性联轴器与电机相连。在靠近电机侧安装正常轴承（即图5中③），远离电机侧安装故障轴承（即图5中⑤），用于模拟各种轴承故障。实验中，利用HG3604故障诊断仪在故障轴承所在轴承座处测取振动加速度信号。

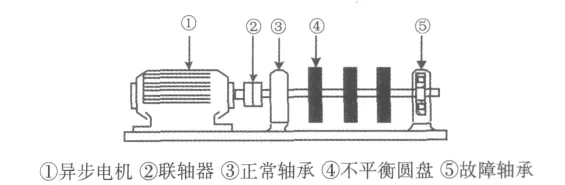
图5 轴承故障模拟实验台Fig.5 Simulation test bench of bearing fault

故障轴承的型号：6 307，轴承的大径：D=80 mm，小径d=35 mm，滚动体个数为8个，压力角α=0，故障类型为：内圈点蚀，故障大小：直径为2 mm，深0.1 mm的点蚀坑，实验台转速R=1 496 r/min，对采集到的轴承内圈故障数据进行分析，采样点数是N=8 192，采样频率fs=6 000×2.56 Hz，通过经验公式计算得到轴承内圈故障特征频率即待检测频率fd=119.246 Hz，差分振子参数：α=0.993，β=0.998，激励频率fe=0.33，放大倍数p=5.5。

从频谱图中几乎得不到任何有用信息，从振子相图中可以看出振子收敛于极环。应用判别准则对差分振子相图的状态进行判别：n1/N=0.020 1，n2/N=0.020 1，可见n2/N＜0.1差分振子相图收敛于极环。无论从差分振子相图还是通过判别准则都说明了信号中待检测频率的存在。

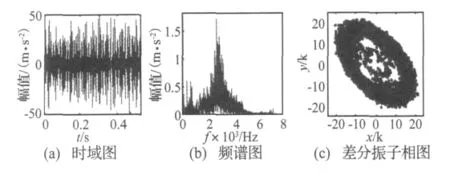
图6 实验数据分析Fig.6 Experimental data analysis

4 工程应用

2008年12月9 日，某高线厂第25架轧机出现振动值超标报警。12月15日开箱检查，发现轴承内圈有严重剥落现象。利用在线监测系统采集到的数据，对这起故障进行分析。这里仅取11月19日至11月21日间的数据进行分析，也就是在线监测系统发出报警前20天左右。其中，采样频率fs=4 000，采样点数N=2 048。图7和图8给出了这3天的振动信号的时域波形及其频谱图。

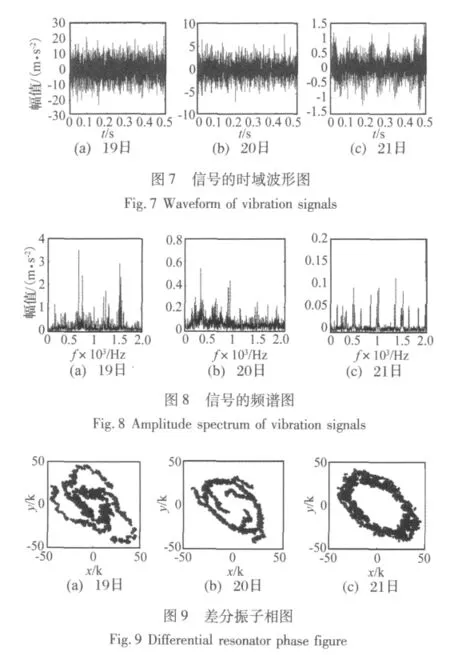
在时域图中没有明显的大的冲击，整体的振动幅值不大。在频谱中无法识别出故障特征频率及其倍频等有用信息。因此我们无法通过时域波形图和频谱获得任何轴承的故障信息。利用差分振子看是否能发现设备故障缺陷以及缺陷的扩展趋势并就差分振子的相图状态进行识别。轴承内圈损伤的特征频率为43.281 Hz，采样点数N=2 048，采样频率fs=4 000。差分振子参数设置如下：检测频率fd=43.281，α=0.995，β=0.999，激励频率fe=0.332 7，放大倍数p=3.5，将数据输入差分振子，观察差分振子相图的变化。

从图9中可以看出，19日的差分振子相图收敛于极点，而20日和21日则收敛于极环，而21日的差分振子收敛的极环要比20日大一些，则说明在21日故障特征频率的幅值比20日要大一些，即故障特征更加明显，故障朝着劣化方向发展。利用差分振子相图状态的判别准则得到的结果如下：图9中（a）：n1/N=0.158 7大于0.1，因此相图收敛于极点。（b）：n1/N=0.005 4远远地小于0.02，收敛于极环说明在20日时就已经出现了故障特征频率。（c）：n1/N=0，远远小于0.02，收敛于极环。

5 结论

根据差分振子相图的特点，给出了差分振子相图的大小与待检测信号幅值间的关系，并在相同的参数条件下，对不同的差分振子相图进行比较分析得出了待检测频率幅值的相对大小。对差分振子的相图进行了识别，根据n1/N（或n2/N）的值来判别差分振子相图的状态。差分振子相图极环的大小反映了待检测信号幅值的大小，从而达到对待检测信号幅值大小的一种定性的判断。将以上方法用来分析工程数据成功地发现了设备故障的发生与发展情况，为设备的安全监测提供了一种有效的方法。

［1］何金群，胥永刚，崔玲丽，等.基于不变矩的Duffing相位图的自动识别［J］.噪声与振动控制，2008，28（5）：80 －82.

［2］魏伟波，芮筱亭.不变矩方法研究［J］.火力与指挥控制，2007，32（11）：114 －117.

［3］商立群，杜亚娟.Hu矩和Zernike矩在图象识别中的应用［J］.西安科技学院学报，2000，20（1）：53－56.

［4］姜 璐，舒华忠，章品正.Hu矩和Zernike矩在表情识别应用中的比较［J］.洛阳大学学报，2004，19（2）：14－17.

［5］ Chen C C.Improved moment invariants for shape discrimination［J］.Pattern Recognition，1993，26（5）：683 －686.

［6］ Mukundan R，Ong S H，Lee P A.Image analysis by tchebichefmoments ［J］.IEEE Transactionson Image Processing，2001，10（9）：1357 －1364.

［7］李 楠，赵东成，李虹波，等.电机转子系统早期故障可视化检测的差分振子法［J］.电力自动化设备，2007，27（6）：74－77.

［8］ Qu L S，Lin J.A difference resonator for detecting weak signals［J］.Measurement，1999，26：69 － 77.