逐步判别分析法在基因表达数据分类中的应用

邹 杨,陈 忠

(长江大学信息与数学学院,湖北荆州434023)

谢俊宇

(洪湖贺龙高级中学,湖北洪湖433200)

利用基因芯片技术测定的基因表达值是一组多变量的高维数据。这些数据可以用于对组织细胞进行分类,也可以用于挖掘对疾病有鉴别意义的特征基因,进而为医学诊断和治疗提供参考。目前,对于此类基因表达数据分类问题有很多研究方法,如线性判别分析法和支持向量机等,线性判别分析比复杂的预测方法效果要好[1]。

在进行判别分类时,不同基因的表达值对于分类结果影响不同。因此,变量 (基因表达值)的选择是一个决定判别效果的关键问题。下面,笔者利用多元统计分析中的逐步判别分析法对基因表达水平数据进行分析。首先,用逐步判别法筛选出了能够区分2个总体的特征基因。然后,基于这些特征基因的表达值数据,利用Bayes判别法建立判别函数,对未知类型的基因表达值数据进行分类。

1 逐步判别分析原理

1.1 判别函数的建立

逐步判别是一种筛选变量的方法。筛选的过程其实就是作假设检验的过程,通过检验找出显著性变量,剔除不显著变量[2,3]。所建立的判别函数中仅保留了对分类判别能力显著的变量。

1.2 判别结果的检验

1)总体均值的检验 假设2总体Gi～N(μi,∑i)(i=1,2),为检验2总体的均值是否有显著性差异(H 0:μ(1)=μ(2)),可以构造F 统计量[4]:

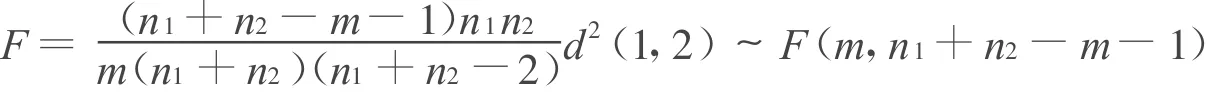
式中,d2(1,2)=(¯X(1)-¯X(2))′S-1(¯X(1)-¯X(2));ni是第i个总体的样品个数(i=1,2)。

计算F统计量的值f,得p=P{F≥f}。若p小于给定的显著性水平a(常取a=0.05),则否定2总体均值相等的假设,即对这2个总体讨论判别问题是有意义的。

2)错判率的估计 利用舍一法 (或称交叉确认法)对错判率进行估计。

2 实例分析

以2001年北京大学校内数学建模竞赛试题 (B题)为实例进行分析。原始数据共60行114列,分别代表60个人和114条基因。其中,有4条基因的表达值完全相同 (分别为原始数据的第37、38、39和40列),这里仅保留其中的一列,故有效检测基因应为111条(记为向量x1～x111)。

数据中,前20行是20个癌症病人的基因表达水平的样本 (记为第0～19组),为分析需要,记其为第1类样本;其后的20行是20个正常人的基因表达信息样本,对应于第20～39组,记为第2类样本;剩余的第40～59组表达值为20个待检测的样本 (未知它们是否正常)。假设原问题所提供的2类样本均来自于正态分布的总体。

2.1 依据特征基因的判别分类

1)特征基因的选取 利用SAS中逐步判别法的命令 “proc stepdisc”完成变量筛选的工作[5]。设定引入变量到判别式的显著性水平为0.10,剔除变量的显著性水平为0.15。通过逐步筛选,最终选出了 32 个 变量, 其序号 为:x1、x5、x8、x12、x18、x20、x24、x25、x27、x36、x37、x39、x57、x58、x60、x67、x69、x71、x72、

x75、x76、x79、x 92、x93、x95、x97、x99、x102、x104、x105、x109和 x111。它们就是能够区分 2 类样本的特征基因。

2)判别过程的实现 在建立判别函数之前,要先对2总体协方差矩阵是否相等进行检验(H0:∑1=∑2)。其中,∑i表示第i个总体Gi～N(μi,∑i)(i=1,2)的协方差矩阵。

利用SAS中的命令 “pool=test”实现对2总体协方差矩阵是否相等进行检验。结果表明,在显著性水平α=0.10时接受了原假设。可以利用合并协方差阵建立判别函数。

依据筛选出的特征基因构成2个新的总体 (其中每一组表达值仅有32个变量)。利用Bayes判别法建立判别函数,对未分类的表达值 (第40～59组)进行判别分类。利用SAS中判别分析的命令 “proc discrim”实现这一过程。该程序输出了Bayes判别函数的系数,则隶属第1(2)类总体的判别函数y1(y 2)分别为:

依据上述判别函数,计算后验概率,对未知类别的基因表达值数据分类。经计算可知,在未知类别的第40～59组基因表达值中,属于第1类总体 (癌症病人)的共有13个,其序号为 {40,42,45,46,47,48,49,51,52,53,54,57,58};属于第2类总体 (正常人)的共有7个,其序号为 {41,43,44,50,55,56,59}。

2.2 判别结果的检验

2个新总体之间的平方距离为385783,其F统计量为22208,相应的p小于0.0001(＜0.01)。这说明利用特征基因构造的2个新的总体,其基因的表达值有显著性差异,讨论判别分类问题是有意义的。利用SAS程序中的 “crosslist”命令对判别分类的结果进行交叉验证 (舍一法),用以估计错判造成的损失。输出结果显示,其错判率为0。

作为对比,利用所有基因的表达值数据构造判别函数,观察其对原训练样本交叉验证的错误率。结果显示,其错误率为20%。

[1]Dodoit S,Fridlyand J,Speed T P.Comparison of discrimination methods for the classification of tumor susing gene expression data[J].Am Stat Assoc,2002,457(97):77-87.

[2]高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005:205-211.

[3]贾云青,侯木舟.Bayes判别分析在医疗数据处理中的应用[J].数学理论与实践,2009,29(2):117-119.

[4]高惠璇.实用统计方法与SAS系统 [M].北京:北京大学出版社,2001:176-178.

[5]何宁,吴黎兵.统计分析系统SAS[M].武汉:武汉大学出版社,2005:261-271.