混沌系统的投影同步在保密通讯中的应用

邓若曦

(武汉理工大学理学院,湖北武汉430070)

自从1963年Lorenz发现混沌吸引子以来[1],混沌动力学作为非线性科学的一个重要分支引起了广大科学技术人员的高度重视。由于混沌具有初值敏感性,人们普遍认为混沌同步非常困难。直到1990年Pecora和Carroll提出了驱动响应同步方法,使Lorenz混沌系统能够实现同步,混沌同步理论和应用才迅速成为一个新的研究热点。近年来,由于混沌同步在保密通信、信号处理、电路设计等领域表现出强劲的应用前景,各国学者高度重视并投入到这一研究领域中来,使得混沌控制和同步方法得到了蓬勃发展[2～10]。笔者针对文献 [11]中的投影同步定义,作了适当的修改,并且分别从同结构和异结构的投影同步来讨论混沌系统在保密通讯的应用,将有用的信号进行加密、掩盖和不失真的恢复。

1 投影同步

定义1 考虑下面2个混沌系统:

式中,xm,xs是2个n维状态向量。‘m'和‘s'代表驱动系统和响应系统,f,g:Rn→Rn是向量值函数。如果存在控制器u,使得:

式中,α为一常数,那么,2个混沌系统(1)完成投影同步。

在系统(1)中,当 f=g,系统(1)就成为同结构的投影同步;当f≠g,系统 (1)就成为异结构的投影同步。在下面的讨论中,笔者从两方面来讨论该方法在保密通讯中的应用。

2 同结构的投影同步应用

采用1996年由Milanovic等提出的改进混沌掩盖保密通信方案[12]。设需要传输的信号为h(t),m(t)=x1+h(t)为发送器和接收器之间的通信混合的叠加信号,该信号分别反馈在发送端和接收端,这样,传输信号的发送端动力学系统为:

式中,a=36,b=3,c=20。接收端为一个同结构的动力学系统:

选取反馈控制器为:

其中 ,e1=αx 2-x1,e2=αy 2-y 1,e3=αz 2-z1。

定理1 当k＞c+a/4时,系统(2)与系统(3)实现同结构投影同步。

证明 由系统(2)与系统(3)有如下误差系统:

当k ＞c+a/4时,˙V ＜0,故误差系统(4)趋于0。

定理1表明,当误差系统(4)趋于零时,则αx 2-x1→0,接收端的恢复信号为h′(t)=m(t)-αx 2=x1+h(t)-αx2→h(t),这意味着同步发生时,发送器发送的信号能够不失真的被接收器接收并恢复,并且只需使用较简单的反馈控制器。

在数值仿真中,设发送端动力学系统(2)与接收端动力学系统(3)的初值分别为(1,2,3),(3,1,5),k=10+c+a/4,α=2。传输的有用信号为h(t)=50的方波信号,es=h(t)-h′(t)为恢复信号与有用信号的误差,仿真结果如图1所示。图1中分别表示传输的有用信号h(t)、叠加信号m(t)、接收恢复端的有用信号h′(t)、恢复信号与有用信号的误差信号。若传输的有用信号为h(t)=7sin(3πt)的正弦信号,相应的仿真结果如图2所示。

图2 正弦信号加密仿真结果

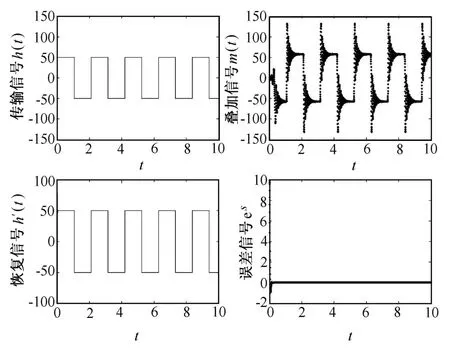
图1 方波信号加密仿真结果

3 异结构的投影同步应用

设需要传输的信号为h(t),m(t)=x1=h(t)为发送器和接收器之间的通信混合的叠加信号,该信号分别反馈在发送端和接收端,这样,传输信号的发送端动力学系统为:

接收端为另一不同结构的动力学系统:

选取反馈控制器为:

定理2 当k＞20+(18×18)/35时,系统(5)与系统(6)实现异结构投影同步。

证明 由系统(5)与系统(6),有如下误差系统:

当k＞20+(18×18)/35时,˙V＜0,故误差系统(7)趋于零。

数值仿真类似于定理1,图3中分别表示传输的有用信号h(t)、叠加信号m(t)、接收恢复端的有用信号h′(t)、恢复信号与有用信号的误差信号。若传输的有用信号为h(t)=7sin(3πt)的正弦信号,相应的仿真结果如图4所示。仿真图验证了该方法的有效性。

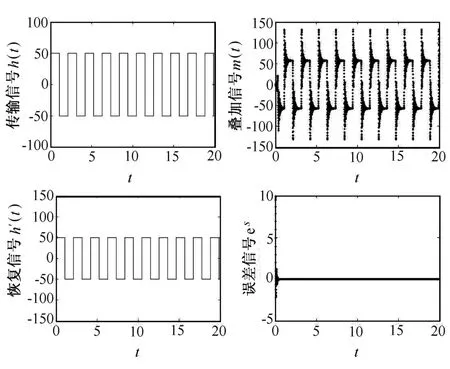
图3 方波信号加密仿真结果

图4 正弦信号加密仿真结果

[1]Lorenz E N.Determ inistic nonperiodic flow[J].Jou rnal of A tmospheric Sciences,1963,20:130-141.

[2]Chen G,Dong X.From Chaos to O rder:Methodologies,Perspectives,and Applications[M].Singapore:W orld Scientific Pub.Co,1998.

[3]Elabbssy E M,Agiza H N,El-Dessoky M M.Adaptive synch ronization of a hyperchaotic system with uncertain parameter[J].Chaos,Solitons&Fractals,2006,30:1133-1142.

[4]LǜJ,Lu A J,Chen S H.Chaotic Time Series Analysis and its Application[M].Wuhan:W uhan University Press,2002.

[5]Chen G,LǜJ.Dynamics of the Lorenz System Family:Analysis,Control and Synchronization[M].Beijing:Scientific Press,2003.

[6]Wang Y,Guan Z H,Wang H.Feedback an adaptive control for the sy nchronization of Chen system via a single variable[J].Physics Letter A,2003,312:34-40.

[7]Pecora L M,Carroll T L.Sy nch ronization in chaotic system s[J].Physical Review.Letters,1990,64:821-824.

[8]Lǜ J,Lu A.Controlling uncertain Lǜ sy stem using linear feedback[J].Chaos Solitons F ractals,2003,17:127-132.

[9]H uang L L,Feng R P,W ang M.Synch ronization of chaotic systems via non linear control[J].Physics Letter A,2004,320:271-275.

[10]Luo R.Impu lsive con trol and synch ronization of a new chaotic sy stem[J].Phy sics Letter A,2008,372:648-653.

[11]Li G.Generalized projective synch ronization between Lorenz system and Lu＇s system[J].Chaos Solitons Fractals,2006,32:1454-1458.

[12]M ilanovic V,Zaghlou l M E.Imp roved masking algorithm for chaotic communications systems[J].Electronics Letters,1996,32(1):11-12.