有限部分变换半群的几类平凡子半群
秦美青
(菏泽学院数学系,山东菏泽274015)
设X是集合,集合X上的所有部分变换在一般映射的合成运算下做成的半群称为部分变换半群[1],记为PX。下面,笔者主要给出当集合X是有限集时,部分变换半群RX的子半群S为R-平凡子半群、L-平凡子半群、J-平凡子半群的充要条件。
1 基本概念
定义1[2]设S为半群,ρ为S上的等价关系,若对每个a,b∈S,aρb⇒a=b,则等价关系ρ称为平凡的。
定义2[3]设S为半群,若对每个a∈S,存在m,r∈IN,使得am+r=am,则称半群S为周期的,特别地,若对每个a∈S,r=1,则半群S称为非循环的。
引理1[4]设S是一个周期半群,则:
1)S是R-平凡的当且仅当对每个a,b∈S,存在m ∈IN,使得(ab)ma=(ab)m。
2)S是L-平凡的当且仅当对每个a,b∈S,存在m∈IN,使得(ab)m=b(ab)m。
3)S是J-平凡的当且仅当对每个a,b∈S,存在m ∈IN,(ab)ma=(ab)m=b(ab)m。
2 主要结果
2.1 PX的R-平凡子半群
设S是PX的子半群,α∈ PX。Fix(α)={x ∈ domα,|xα=x},Fix(S)={Fix(α)|α∈ S}。
定理1 设S是PX的子半群,则S是R-平凡的当且仅当对每个α,β∈S,有Fix(αβ)=Fix(α)∩Fix(β)。
证明 设S是R-平凡的。因为X是有限集,所以S是周期半群。任取 x∈ Fix(αβ),则x∈dom(αβ)。由 dom(αβ)=(imα∩ domβ)α-1⊆domα,故 x ∈ domα。因为 x ∈ Fix(αβ),所以 x=xαβ∈ dom(αβ),这样 x=xαβ=(xαβ)αβ=x(αβ)2,又因为 x=x(αβ)2∈ dom(αβ),所以 x=xαβ=[x(αβ)2]αβ=x(αβ)3,依次类推有 x=xαβ =x(αβ)m,再由引理 1 知 x=xαβ =x(αβ)m=x(αβ)mα=xα,即 x ∈ Fix(α)。因为x=xα且xα∈ domβ,所以 x=xαβ=xβ,即 x ∈ Fix(β)。从而对任意 x ∈ Fix(αβ),有 x ∈ Fix(α)且 x ∈Fix(β),故 Fix(αβ)⊆Fix(α)∩ Fix(β)。
任取 x ∈ Fix(α)∩ Fix(β),则 x ∈ domα∩ domβ且xβ =x=xα∈ domβ,这样 xαβ =xβ =x,即x ∈ Fix(αβ),故对任意 x ∈ Fix(α)∩ Fix(β),有 x ∈ Fix(αβ),从而Fix(α)∩ Fix(β)⊆Fix(αβ),这样就有Fix(αβ)=Fix(α)∩ Fix(β)。

反之 ,设 α,β ∈ S 且 αRβ,则存在 γ,δ∈ S,使得 α=βγ,β=αδ。因为:所以 domα=domβ。任取 x ∈ domα=domβ,则 xα=xαδγ,即 xα∈ Fix(δγ)。再由对每个 α,β∈ S,有Fix(αβ)=Fix(α)∩ Fix(β),故 xα=Fix(δ)∩ Fix(γ),从而 xα=(xα)δ=xβ,即对任意 x ∈ domα=domβ有 xα=xβ,从而 α=β,故S 是R-平凡的。
2.2 PX的L-平凡子半群
定义3[5]设α∈PX,则由等价关系W(α)={(x,y)∈domα×domα|xαs=yαt,对某个s,t≥0}确定的等价类称为α的轨迹。α的所有轨迹做成的集合记为Ψ(α)。
定义4[6]设 Xi∈ Ψ(α),集合{x ∈ Xi|xαr=x,对某个r>0}称为 Xi的kernel,记为K(Xi)。
定理2 设 α∈PX,则 α是非循环的当且仅当对每个Xi∈ Ψ(α),|K(Xi)|=1。
证明 设 α∈PX是非循环的。任取x∈K(Xi),由K(X i)得定义知,存在 s>0,使得 xαs=x,则(xαs)αm+1-s=xαm+1-s,从而 xαm+1=(xαm)α1-s,因为 α是非循环的 ,所以 xαm+1=xαm,则s=1,故 xα=x。若存在y ∈ K(Xi),则 x,y ∈ Xi⊆Ψ(α),即存在s1,s2 >0,使得 x=xα=…xαs1-1=xαs1=yαs2=yαs2-1=… =yα=y,从而|K(Xi)|=1。
反之,假设对每个Xi∈ Ψ(α),|K(Xi)|=1。因为|K(Xi)|=1,所以任意 x ∈ K(Xi),有 x=xα,否则 ,存在 r >0,使得 xαr=x,这样 xαr+1=xα,即(xα)αr=xα,从而 xα∈ K(X i)与|K(Xi)|=1矛盾 。对任意 x ∈ K(X i),显然存在m,使得xαm+1=xαm,不妨设m充分大。任取 y且满足(x,y)∈ W(α),则存在 s,t >0,使得 xαs=yαt。
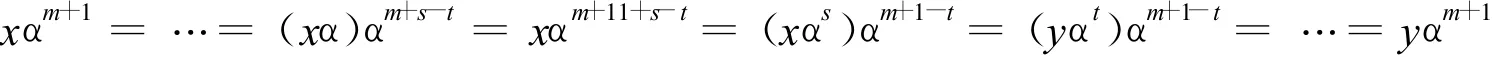
相似可证 ,xαm=yαm。因为 xαm=xαm+1,所以 yαm=yαm+1,故 αm=αm+1,从而 α∈ P X 是非循环的。
从定理2容易得出若α是非循环的,则(x,y)∈W(α),当且仅当 xαm=yαm,其中,m为充分大整数。
定理3 设S是P X的子半群,则S是L-平凡的当且仅当对每个α,β∈S,有W(αβ)=W(α)∨ W(β)。
证明 在整个证明过程中m表示充分大整数。假设S是L-平凡的,则S是非循环的且对每个α,β∈S,有(αβ)m=β(αβ)m。设(x,y)∈ W(αβ),则 x,y ∈ dom(αβ)⊆domα且 x(αβ)m=y(αβ)m。因为S 是非循环的且 x ∈ domα,xα∈ domβ,所以 xαm+1=xαm,即(xα)αm=xαm,故(x,xα)∈ W(α)。因为(xα)βm=(xα)βm+1=(xαβ)βm,所以(xα,xαβ)∈ W(β)。因为(xαβα)αm=(xαβ)αm+1=(xαβ)αm,所以(xαβ,xαβα)∈W(α)。依次类推有(x(αβ)m-1α,x(αβ)m)∈ W(β)。这样就有(x,x(αβ)m)∈ W(α)∨ W(β)。相似可证(y,y(αβ)m)∈ W(α)∨ W(β)。因为 x(αβ)m=y(αβ)m,所以(x,y)∈ W(α)∨ W(β),从而 W(αβ)⊆W(α)∨W(β)。因为 x ∈ dom(αβ)m=domβ(αβ)m=dom(βα)mβ ⊆dom(βα)m且S 是非循环的子半群,所以(βα)m=(βα)m+1,故 x ∈ dom(βα)m+1。进一步有 x(βα)m+1=xβ(αβ)mα=x(αβ)mα=y(αβ)mα=y(βα)m+1,故(x,y)∈ W(βα),从而 W(αβ)⊆W(βα)。相似可证 W(βα)⊆W(αβ),这样就有 W(βα)=W(αβ)。不妨设 x,y ∈dom(αβ)m=domβ(αβ)m⊆domβ,且(x,y)∈ W(β),则 x(αβ)m=xβ(αβ)m=xβm(αβ)m=yβm(αβ)m=y(αβ)m,这样有(x,y)∈ W(αβ),从而 W(β)⊆W(αβ)。相似可证 W(α)⊆W(βα)=W(αβ),故 W(α)∨W(β)⊆W(αβ),这样就有 W(αβ)=W(α)∨ W(β)。
反之 ,假设对每个 α,β ∈ S,有W(αβ)=W(α)∨ W(β),则 W(α)=W(α2)=W(α3)= …,从而 S 是非循环的。事实上,若对任意 x ∈ domα,有 xαr=x且xα≠x,则对每个 s,t≥0,有 x(αr)s=x ≠xα=xα(αr)t,这样有(x,xα)∈ W(α)但(x,xα)∉ W(αr)与 W(α)=W(αr)矛盾。因为对每个 x ∈ domβ和每个 α,β∈ S 有(x,xβ)∈ W(β)⊆W(αβ),则 x ∈ dom(αβ)m且又因为S 是非循环的,所以对每个 x ∈dom(αβ)m,有 x(αβ)m=xβ(αβ)m,即(αβ)m=β(αβ)m,故 S 是L-平凡的 。
2.3 PX的J-平凡子半群
定理4 设S是P X的子半群,则S是J-平凡的当且仅当对每个α,β∈S,有:

证明 首先说明因为X是有限集,所以S是有限半群,从而是周期半群,故在S上J=D。
假设S是J-平凡的。任取α,β∈S且αRβ,则αJβ。因为S是J-平凡的,从而α=β,故S是R-平凡的,由定理 2知 Fix(αβ)=Fix(α)∩ Fix(β)。相似可证 ,任取α,β∈ S 且αLβ,则 αJβ。因为 S 是J-平凡的,从而α=β,故 S 是J-平凡的,由定理3知 W(αβ)=Fix(α)∩ Fix(β)。
反之 ,假设每个 α,β∈ S,有 Fix(αβ)=Fix(α)∩ Fix(β),W(αβ)=Fix(α)∩ Fix(β),任取 α,β∈ S,且αJβ ,则存在 γ∈ S,使得 αRγ,γLβ,由假设知,Fix(αβ)=Fix(α)∩ Fix(β),W(αβ)=Fix(α)∩ Fix(β)。再由定理2和定理3知α=β=γ,从而S是L-平凡的。
[1]Saito T.J-trivial subsemigroupsof finite full transfirmation semigroups[J].Semigroup Forum,1998,57:60-68.
[2]How ie J M.P roudu ctsof idem potent in finite full transformation sem igroups[J].Proc Royal Soc Edinburgh A,1980,86:243-254.
[3]Umar A.On the sem igroups of order-decreasing finite full transformations[J].Proc Royal Soc Edinburgh A,1992,120:129-142..
[4]How ie J W.An introduction to sem igroup Theory[M].London:Academ ic Press,1976.
[5]秦美青,许新斋.关于部分变换半群的一类子半群 [J].山东师范大学学报 (自然科学版),2009,24(1):6-9.
[6]许新斋,许四军,毛娟,等.关于序半群的结构与理想[J].山东师范大学学报(自然科学版),2008,23(1):4-6.
——评《其精甚真——高校学生思想政治教育理论与实践》

