(k,q)平坦数列研究
朱尧兴
(南京铁道职业技术学院苏州校区,江苏苏州215137)
从1到n的n个自然数进行排列,可以有各种各样的排列。设S={1,2,3,…,n},将这n个数排成一环形数列:a0,a1,a2,a3,…,an-1,ai∈S,记 Ai=ai+ai+1+…+ai+k-1,其中i+k-1(mod n),0≤i≤n-1,值达到最小值,记作LS(n,k,q),那么称此排列为(k,q)-平坦数列。显然,这样的排列与n,k和q都有关系。例如,n=5时,有12种不同的环形排列,其中LS(5,2,2)=184,LS(5,3,2)=409,LS(5,3,3)=3753,非常巧合的是,达到这些下限值的排列均为:1,5,2,3,4。对于一般的n,k和q,下面笔者给出了一些性质。
1 (k,q)-平坦数列的几个性质
性质1(平凡性) 对于任意的排列,有:
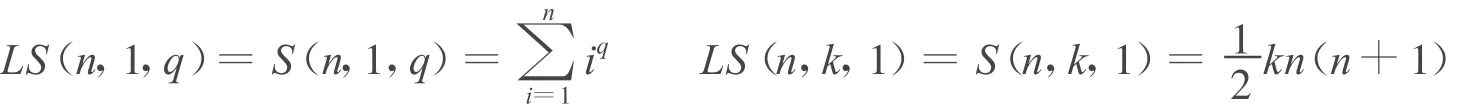
由定义可容易得到上述性质。
性质2(单调性) 如果排列C使和值S(n,k,q)达到LS(n,k,q),那么该排列必也能达到LS(n,k,q+1),反之亦然,对于q>1,k>1,n>3。
证明 设排列C:a0,a1,a2,a3,…,an-1是取得LS(n,k,q)的排列,那么对于其他任意的排列C′:a′0,a′1,a′2,a′3,…,a′n-1 都有于 A′i,Ai ≥1,i=0,1,…,n-1,成立。反之亦然。
性质3(周期性) 如果排列C使和值S(n,k,q)达到LS(n,k,q),那么必也能达到LS(n,n+k,q),反之亦然。
证明 设排列C:a0,a1,a2,a3,…,an-1是取得LS(n,k,q)的排列,那么对于其他任意的排列C′:a′0,a′1,a′2,a′3,…,a′n-1都有:

下面计算:

则:
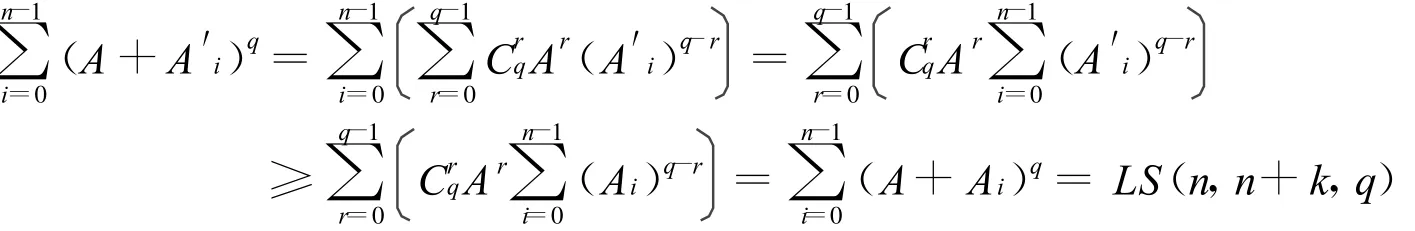
性质4(互补性) 当q=2时,如果排列C使和值S(n,k,2)达到LS(n,k,2),那么必也能达到LS(n,n-k,2),反之亦然。
证明 设排列C:a0,a1,a2,a3,…,an-1是取得LS(n,k,2)的排列,那么对于其他任意的排列C′:a′0,

即该排列也使达到LS(n,n-k,2)值。
2 LS(n,2,2)的值及其对应的排列
当q=2,k=2时:

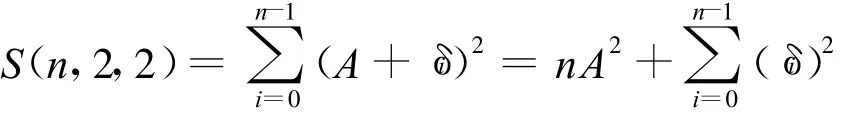

下面来选取适当的排列使满足式(1),从而使值达到LS(n,2,2):
从n开始考虑,则n的左右两侧分别取1和2,这样能满足(1)的条件(而且是唯一的),然后在1的左侧取(n-1),2的右侧取(n-2),同样满足条件 (1),如果换成其他的数,则不能满足条件 (1),所以这是最合适的。依次地以式(1)为条件选取数,直至结束,由这样的取法可知是满足式 (1)的唯一排列 (如图1)。

图1 排列图
容易计算:

其中,当n为奇数时,ε=1;当n为偶数时ε=2。
3 k>2,q=2值的部分结果
对于k>2,q=2的一般情形,尚未有结果,笔者通过计算机计算了部分情形,如表1。

表 1 k>2,q=2的部分结果
由表1可知,当n增大时,达到最小值的排列不唯一。显然,随着n的增加,计算机搜索的量飞速增长,因此探求一般的排法,很有价值。
[1]曹汝成.组合数学 [M].广州:华南理工大学出版社,2002.
[2]Brualdi R A.组合数学 [M].冯舜玺 等译.北京:机械工业出版社,2002.

