CB－1200型动平衡机主轴应力仿真计算

欧儒春

（1.重庆大学，重庆 400045;2.重庆电力高等专科学校，重庆 400053）

0 引言

平衡机是测量旋转物体(转子)不平衡量大小和位置的机器。平衡机主轴是平衡机最主要的部件，主轴设计的好坏直接关系到平衡机性能的好坏，因此对平衡机主轴进行计算和分析是十分必要的。本文以工程应用为背景，基于应力分析的强度理论，应用有限元分析软件对CB1200型平衡机主轴进行了在外力作用下的应力分析。

1 强度理论

1.1 最大拉应力理论

这一理论认为最大拉应力是引起材料断裂的主要因素。也就是说，不论是多轴应力状态，还是单轴应力状态，引起断裂的因素是相同的，均为最大拉应力σ1，只要最大拉伸应力达到材料的强度极限σb，就会引起断裂［1－2］

按该强度理论建立的强度条件是

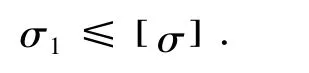
1.2 最大伸长线应变理论

该理论认为最大伸长应变ε1是引起材料断裂的主要因素。也就是说不论何种应力状态，引起断裂的因素是相同的，均为最大拉伸应变ε1，只要最大拉伸应变达到材料的应变极限εb就会引起断裂。

按照该强度理论建立的强度条件是

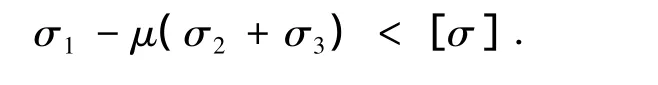
1.3 最大剪应力理论

该理论认为最大剪应力是引起流动破坏的主要因素。也就是说不论何种应力状态，最大剪应力τmax是引起流动破坏的因素。在单轴拉伸应力作用下，当横截面上的拉伸应力达到屈服极限σs时，与轴线成45°的斜面上的最大剪应力为

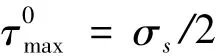
按照这一理论建立的强度条件是

这一理论较为满意地解释了塑性材料出现塑性变形现象，且形式简单，概念明确，所以在机械结构中得到广泛应用。在该理论中，由于忽略了中间应力σ2的影响，使得在二轴应力状态下，按该理论所得结果与试验结果相比偏于安全。

1.4 形状改变比理论

该理论认为形状改变比能是引起材料流动破坏的主要原因。因此，不论材料处于何种应力状态，只要形状改变比能达到单向拉伸屈服时的形状改变比能，材料就发生流动破坏［3］。

在单轴应力状态下，当界面上的拉伸应力达到屈服极限σs时，材料就发生流动破坏。

按该强度理论建立的强度条件是

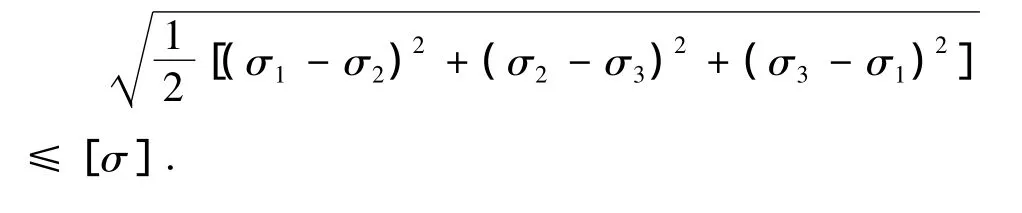
如果已知方向应力，其强度条件为

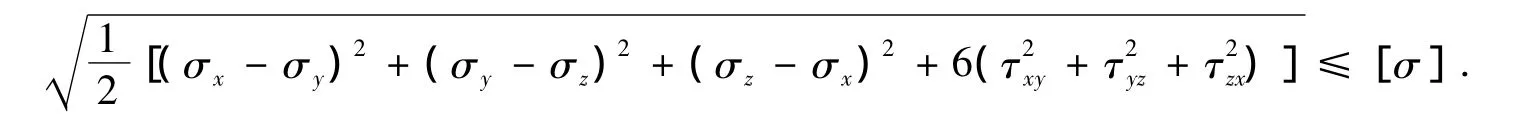
综合上述四个强度理论的强度条件，可以写成同样的形式:

σcr≤［σ］

式中，σcr为当量应力或等效应力，由三个主应力按一定的形式组合而成。

按照从第一强度理论到第四强度理论的顺序，等效应力分别为

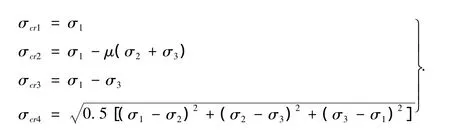
在有限元计算中，按照第四强度理论给出的等效应力通常称为von_Mises应力。

四种常用的强度理论中，第一和第二强度理论适用于脆性材料，如铸铁、混凝土、玻璃等，在通常情况下这些材料以断裂的形式破坏;第三和第四强度理论适用于塑性材料，如碳钢、铜、铝等，在通常情况下这些材料以流动形式破坏。

2 模型建立及前处理

通过对动平衡机主轴测绘，得到主轴尺寸数据参数，应用PRO/E软件建立主轴三维模型。材料属性为:弹性模量输入2.06×1011g/mm·s2，泊松比输入0.3;密度输入7.8×10－3g/mm3。将建好的三维模型导入ANSYS软件划分等效节点和单元，本文网格的划分采用Solid45实体单元，Solid45实体单元是8节点六面体单元。任意直边8节点六面体单元的每条边界坐标线性变化，满足单元的完备性要求。

划分网格的结果，共采用了62212个Solid45实体单元，节点总数为15282个，如图1所示。

3 应力计算

3.1 载荷的计算

平衡机静态时对主轴施加的载荷有固定在托盘上的轮胎重力，两个主轴承的支撑力和带轮所受皮带的预紧力。由于托盘及带轮的质量远小于轮胎的质量，所以忽略托盘及带轮自身的重力。

计算式采用最大极限计算方法，根据平衡机厂家提供数据，最大可进行平衡轮胎重量为65 kg，所以托盘所受的轮胎自身重力作用为637N。

图1 主轴网格划分图

3.2 皮带预紧力的选取

根据平衡机厂家提供数据，皮带预紧力最小值不能小于150N，所以皮带预紧力选用150N，由于皮带是以一定的角度包裹在皮带轮上，并且两边为对称布置，所以力在施加的时候只选择皮带轮上端最高点作为力的施加点［4］。

3.3 载荷的施加

根据主轴实际运行状态进行载荷施加状态的简化，载荷施加及约束如图2所示。

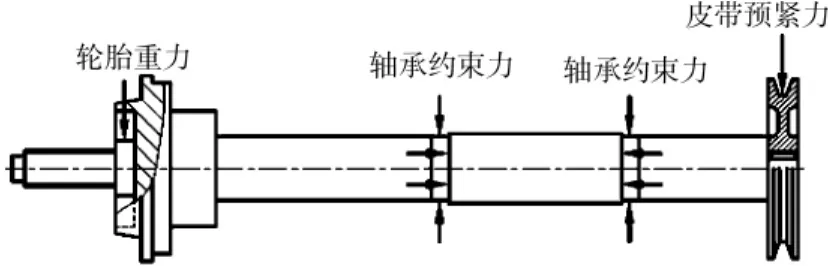
图2 载荷施加示意图

3.4 计算结果

加载后进行仿真计算，可以得到主轴各部分的应力情况，整体等效应力分布云图、主轴最大拉应力和压应力处分布云图，分别如图3、图4、图5所示。

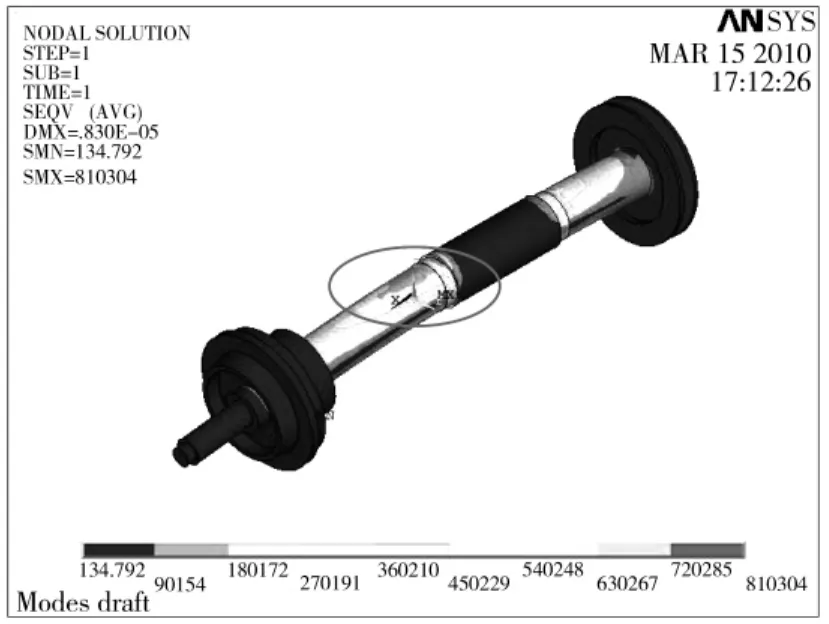
图3 主轴整体应力分布云图

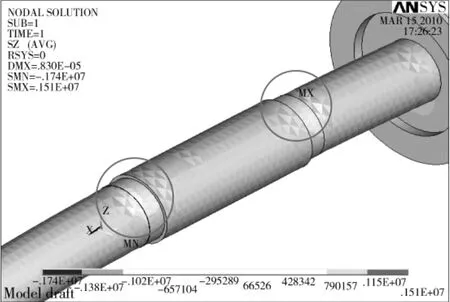
图4 主轴最大拉应力处分布云图

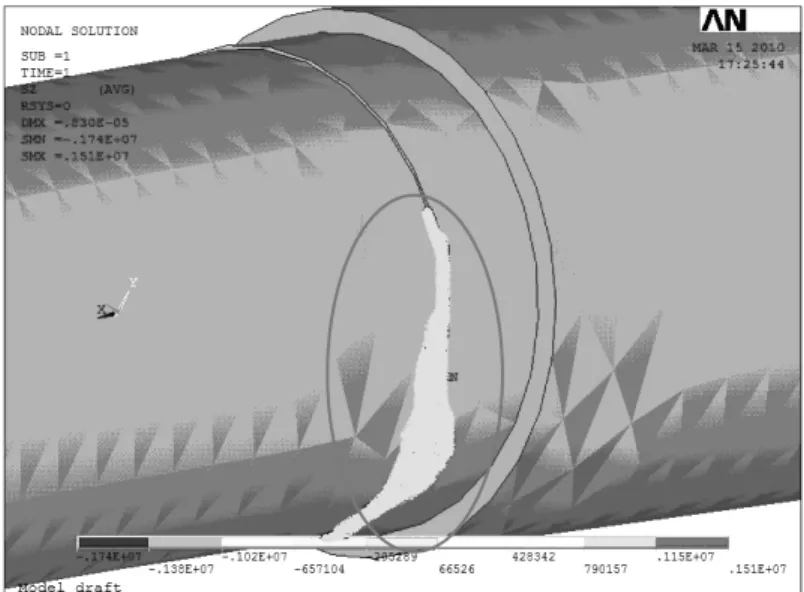
图5 主轴最大压应力处分布云图

由计算结果可以看出最大拉应力和最大压应力出现在轴承安装位置，根据第四强度理论及等效应力公式可知等效应力为:0.81MPa。

4 结论

经过计算主轴在加载轮胎重力和带轮预紧力的作用下，由图4主轴最大拉应力处分布云图可以得出主轴最大拉应力为1.51MPa;由图5主轴最大压应力处分布云图可以得出最大压应力为1.74MPa;45钢最大许用应力为［σ］=600MPa，经过对比可以看出，主轴在静载荷作用下，最大拉压应力都远小于许用应力。因而平衡机主轴在正常工作时应力满足强度要求。

［1］ 高德平.机械工程中的有限元法基础［M］.西安:西北工业大学出版社，1993.

［2］ 徐涛.数值计算方法［M］.长春:吉林科学技术出版社，1998.

［3］ 张汝清，詹先义.非线性有限元分析［M］.重庆:重庆大学出版社，1990.

［4］ 许焕然，倪行达，王裴.工程中的有限元方法［M］.长春:吉林工业大学出版社，1985.