轿车车门的模态计算和组合式优化分析

肖成林，周德义，王志明 ，杨翔宇

(1.吉林大学 生物与农业工程学院，吉林 长 春 130022;2.吉林大学机械科学与工程学院，吉林长春 1300222;3.吉林大学汽车工程学院，吉林长春 130022)

轿车车门的模态计算和组合式优化分析

肖成林1，周德义1，王志明2，杨翔宇3

(1.吉林大学 生物与农业工程学院，吉林 长 春 130022;2.吉林大学机械科学与工程学院，吉林长春 1300222;3.吉林大学汽车工程学院，吉林长春 130022)

以模态分析理论为基础，通过有限元软件HyperWorks对车门进行了模态分析，考察了该车门的刚度特性;并用拓扑优化中的变密度法，通过HyperWorks对轿车车门进行了拓扑与形貌的组合分析，得到了高刚度、轻质量的设计方案。

轿车车门;有限元;Opstruct;模态分析;组合优化

轿车车门骨架的质量和结构形式直接影响车身总成的寿命和性能。汽车结构设计中，在满足车辆运营中对车身的刚度、强度、舒适性及工艺改造等因素要求的同时，应当尽可能减轻车身的质量和降低制造成本。车门结构设计的主要目的在于在确保车门强度、刚度和舒适性的前提下，减轻车门骨架的质量，缩短新产品开发周期。

笔者针对某轿车车门的结构特点，首先对其进行了自由模态分析，求解了车门前7阶约束模态的固有频率及相应振型，为分析车门振动响应作了必要准备，为改进车门的结构设计提供了一定的理论依据。结构的拓扑优化由于其理论和计算上的复杂性而成为结构优化设计中最富挑战性的研究领域［1］。笔者又对轿车车门进行了拓扑与形貌的组合分析，得到了高刚度、轻质量的设计方案。

1 轿车车门几何模型的简化和建立

经过对非承载构件、装饰件、非主要受力结构中孔以及连接关系的简化，用CATIA软件建立了用于有限元模拟仿真分析的车门几何模型，如图1。

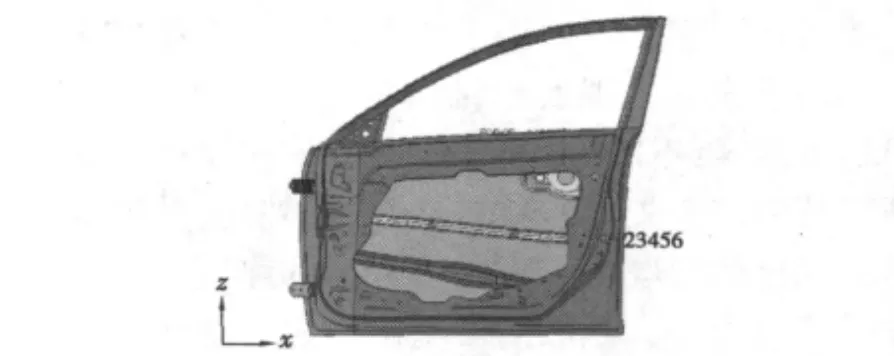
图1 轿车车门结构简化的几何模型Fig.1 The structure simplified geometric model of car door

2 轿车车门有限元模型的建立

2.1 几何模型的前处理

在车身的详细设计阶段，建立基于几何模型的详细有限元模型，根据载荷工况和车门的响应特性，用板壳单元模拟计算。

车门构件的模型与参数如表1、图2。

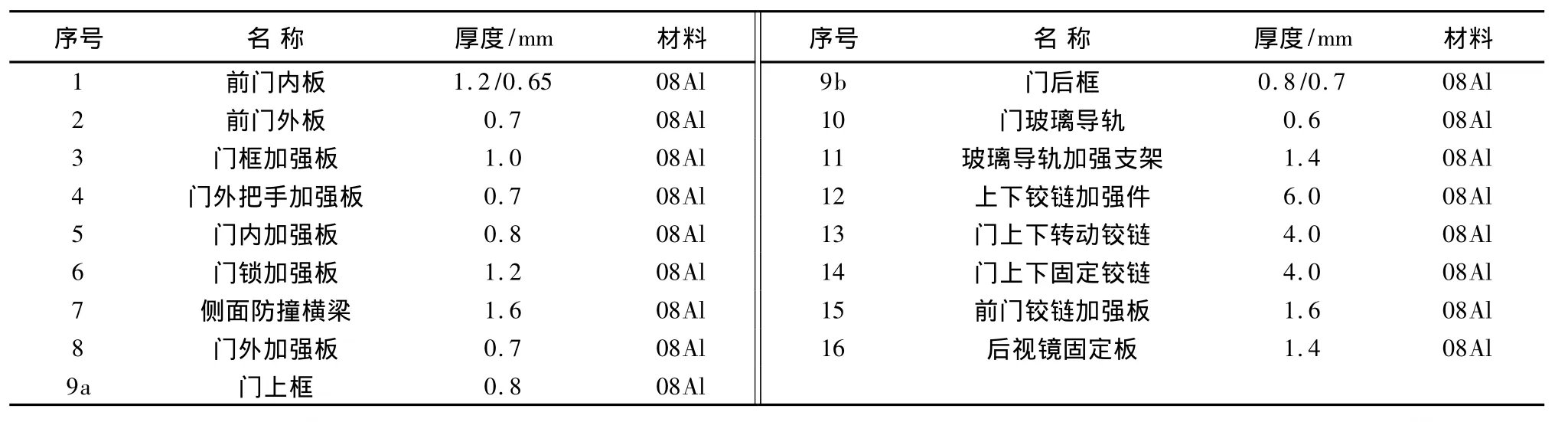
表1 车门构件名称及参数Tab.1 The component name and parameter list of door

图2 车门构件爆炸Fig.2 The exploded view drawings of door components

车门构件的材料为08Al，08A1是冷扎钢板，其材料特性:弹性模量E=206.8 GPa，泊松比μ=0.3，密度ρ=7.9 ×103kg/m3，屈服极限σs=275 MPa，强度极限 σb=410 MPa。

2.2 轿车车门有限元模型的确定

对初步建立的模型进行了调整。模型修正的基本原则是充分体现实际结构的主要关键力学特性，即尽可能详细模拟对整体抗弯和抗扭刚度贡献大的筋等结构。首先，进行单元网格规整化，并减少三角形单元比例;其次，修正门口翻边的厚度;最后，对初步试算应力较大区域的模型网格进行细化。

根据该车门结构，利用HyperMesh对几何模型进行了以下处理:

1)焊点主要采用REB 2的方式模拟，部分采用REB 3的方式模拟;

2)车门所有零件都用板单元进行离散，尽量采用四边形单元。

建立的有限元模型如图3，模型节点总数为23 287，单元总数为21 329，自由度数为132 792。

轿车车门结构材料参数如表2。

表2 轿车车门材料参数Tab.2 The material parameters of car door

图3 车门有限元模型Fig.3 Finite element model of the door

3 轿车车门的模态分析［2］

3.1 设计目标与要求

根据轿车车门的功能要求，其主要部件需要满足如下的设计要求:

1)轿车车门外侧的部件设计要平整、光滑且易加工，使其与车身完美结合，看上去更美观;

2)与车门门框接触的部件设计要精确易加工，使其与门框接触良好，且不产生噪声;

3)轿车车门内侧较大的部件设计要质量最轻，使其最大限度地减少车门整体的质量;

4)轿车车门壳单元的厚度要小于5 mm，使其更符合实际加工情况。

3.2 车门的模态分析

采用Lanczos算法［3-4］提取了该车门骨架的低阶非刚体模态，对整个车门骨架在计算时不施加任何约束，即对有限元模型进行自由状态下的模态提取，应用Opstruct模块计算得到前7阶的自由模态结果如表3。

表3 轿车车门的前7阶固有频率Tab.3 The first seven bands natural frequency of car door

与表3对应的前7阶振型见图4～图10。

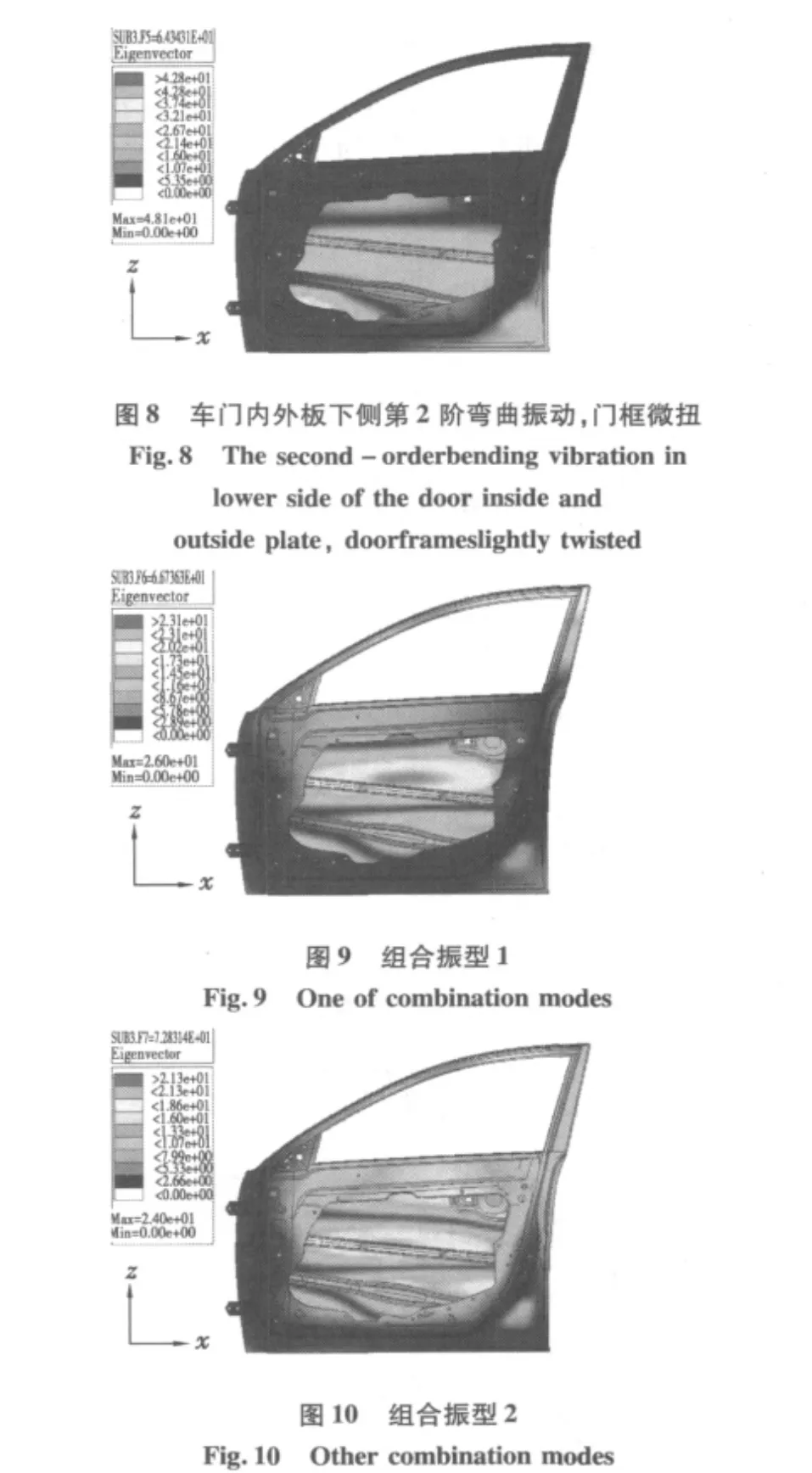
由表3的模态结果看出，车门的第1阶弯曲振型频率是31.91 Hz，其值略高于国内同类车的车门骨架的1阶扭转频率(27.8 Hz)，这一频率值已经大大减小了车门骨架结构与车身及传动系统之间共振的可能性［5］。由图4的振型结果可以知道，门上框和门后框的变形较大，门外把手加强板和门内加强板的变形较小，其它部件基本没有变形，振动多集中在车门的上半部位，对整体结构的影响不大，可以视研究的具体情况给与结构的改进优化，以便得到该车门骨架较为合理的刚度分布情况和模态参数值。

从上面的分析及考虑到轿车车门强度的要求，不能通过修改尺寸来大幅度提高第1阶固有频率，所以在不改变设计结构的前提下，通过改变尺寸参数来提高固有频率是行不通的;只能通过改变设计来提高固有频率。

4 轿车车门的组合式优化分析

拓扑优化可在给定的设计空间内找到最优的材料分布;形貌优化可在钣金件上找出最佳的加强肋位置和形状。笔者采用变密度法，运用有限元软件Opstruct对轿车车门进行了拓扑与形貌的组合分析［6］。

4.1 问题描述

1)设计目标:

使轿车车门获得最大的刚度。

2)设计约束:

第1阶模态的频率的最低要求为28 Hz。

3)设计变量:

设计空间中单元密度和形状变化。

4.2 优化过程

在OpiStruct中优化分析的主要过程［7］:

1)设置有限元模型;

2)施加载荷和边界条件;

3)设置优化参数;

4)提交作业;

5)查看结果及分析。

由于轿车车门实际工况的限制以及某些必须满足的设计参数，使得车门的可优化区域受到了严格的制约，综合考虑本论文只对其内侧的3个大的主要部件(部件1:车门内板;部件7:侧面防撞横梁;部件8:门外加强板)进行优化(图2)，得优化区域如图11。

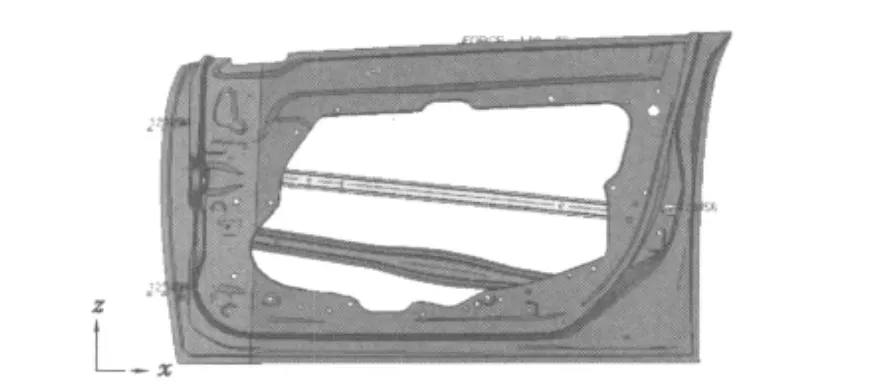
图11 优化部件Fig.11 The diagram of Optimized parts

4.3 组合优化结果

图12为HyperGraph［8］模拟出的目标函数迭代次数的曲线，共迭代6次。

图12 目标函数随迭代次数的曲线Fig.12 The curve of objective function with the number of iterations

图13(a)～图13(f)为6次迭代的结果。

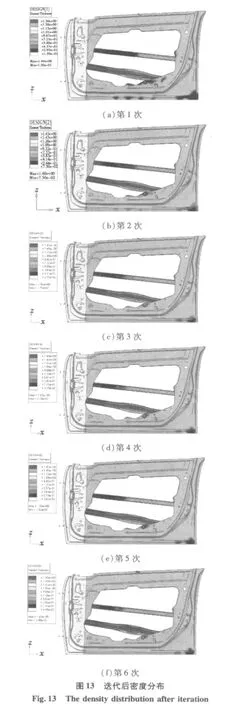
图14(a)～14(c)为第6次迭代的不同密度下的等值面图。

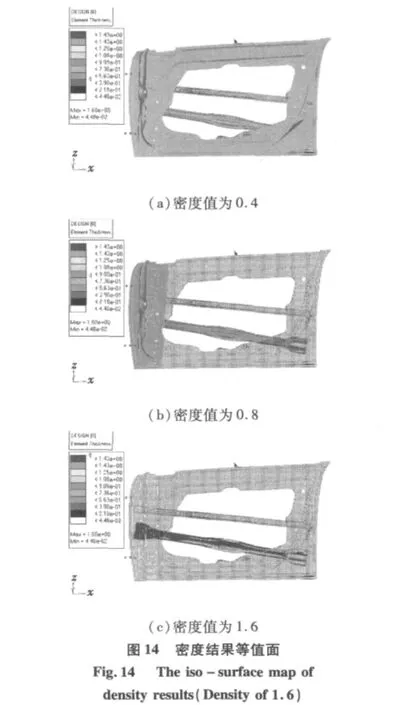
本文采用的拓扑优化方法为变密度法。由6次迭代的密度分布图和第6次迭代的密度结果等值面云图知:密度小的部位越来越少，最后集中在门内板上方中部和后下角、门外加强板的前半段，所以设计时适当减小其厚度;密度大的部位集中在车门内板前半部分和侧面防撞横梁上，设计时应添加不同形式的加强板。这3个部件的密度分布图与模态分析的结果相对应:密度分布图中密度大的部位对应模态分析图中振动大的部位，密度小的部位对应振动小的部位。图中密度大的部位优化后厚度适当增加或通过加强板增加了其强度，密度小的部位优化后厚度减小，可见得到满意的结果。

5 结论

1)使用大型CAD软件CATIA建立简化的几何模型，同时利用大型有限元HyperWorks中的HyperMesh模块对几何模型做相应的前处理得到有限元模型。

2)应用Opstruct模块计算得到前7阶的自由模态结果，分析及考虑到轿车车门强度的要求，可知不能通过修改尺寸来大幅度提高第1阶固有频率，所以在不改变设计结构的前提下，通过改变尺寸参数来提高固有频率是行不通的;只能通过改变设计来提高固有频率。

3)运用Optistruct模块做了组合式优化设计，得到刚度强、质量轻的设计方案，能加速企业开发产品过程，缩短产品开发周期，提高产品质量。

［1］冯桢，于涛，曾齐福.拓扑优化方法在产品设计中的应用探索［J］.机械设计与制造，2007(3):138-139.

FENG Zhen，YU Tao，ZHENG Qi-fu.Application and attempt of topology optimization in design［J］.Machinery Design＆ Manufacture 2007(3):138-139.

［2］王得刚，赵春雨，闻邦椿.基于HyperMesh的车身模态分析［C］∥第三届中国CAE工程分析技术年会论文.大连:［出版社不详］，2007:395-402.

［3］ 陈塑寰.结构振动分析的数值方法［M］.长春:吉林科学技术出版社，1996.

［4］徐涛，程飞，于澜，等.基于预条件Lanczos算法的结构拓扑修改静态重分析方法［J］.吉林大学学报:工学版，2007，5(37):1214-1218.

XU Tao，CHENG Fei，YU Lan，et al.New method for structural static reanalysis of topological modifications bsed on preconditioning Lanczos algorithm［J］.Journal of Jilin University:Engineering and Technology Edition ，2007，5(37):1214-1218.

［5］高云凯，兰晓里.轿车车身模态修改灵敏度计算分析［J］.汽车工程，2001，5(23):352-355.

GAO Yun-kai，LAN Xiao-li.The sensitivity analysis of car body modal.modification［J］.Automotive Engineering，2001，5(23):352-355.

［6］刘庆，侯献军.基于HyperMesh/OptiStruct的汽车零部件结构拓扑优化设计［J］.装备制造技术，2008(10):42-44.

LIU Qing，HOU Xian-jun.Structure topology optimization design of vehicle parts based on HyperMesh/OptiStruct［J］.Equipment Manufacturing.2008(10):42-44.

［7］张胜兰，郑冬黎，郝琪，等.基于HyperWorks的结构优化计技术［M］.北京:机械工业出版社，2007.

［8］于开平，周传月，谭惠丰，等.HyperMesh从入门到精通［M］.北京:科学出版社，2005.

Mode Calculation and Combined Optimization of Car Door

XIAO Cheng-lin1，ZHOU De-yi1，WANG Zhi-ming2，YANG Xiang-yu3
(1.Biological and Agricultural Engineering College，Jilin University，Changchun 130022，China;
2.Mechanical Science and Engineering College，Jilin University，Changchun 130022，China;
3.College of Automotive Engineering，Jilin University，Changchun 130022，China)

Based on the modal analysis theory and FEM software HyperWorks，analysed low-order modes on founded fem model，so as to preferably investigates the door's stiffness characteristics.Based on the variable density method of topology optimization.Based on analysis of the combination of topology and morphology，it can be obtained a design scheme of high rigidity and light mass.

car door;fem;Opstruct;modal analysis;combinatorial optimization

U463.834

A

1674-0696(2011)03-0465-05

2011-01-29;

2011-03-16

科学技术部科技人员服务企业项目(2009GJB10036)

肖成林(1984-)，男，河南商丘人，硕士，主要从事农业机械部件强度分析与优化的研究工作。E-mail:xiaochenglin163@sohu.com。