基于接触理论的矮塔斜拉桥索塔锚固区应力分析
宋 军,王福敏,耿 波,胡 景,周 嫚,赵艳磊
(1.重庆交通大学 土木建筑学院,重庆 400074;2.招商局重庆交通科研设计院有限公司,重庆 400067)
基于接触理论的矮塔斜拉桥索塔锚固区应力分析
宋 军1,王福敏2,耿 波2,胡 景2,周 嫚1,赵艳磊1
(1.重庆交通大学 土木建筑学院,重庆 400074;2.招商局重庆交通科研设计院有限公司,重庆 400067)
利用大型有限元软件对矮塔斜拉桥分丝管式的索塔锚固区建立了非线性接触模型,通过定义模拟拉索与鞍座的接触关系,探讨了鞍座处混凝土的应力分布情况和索力传递分配情况,并与等效线荷载计算模型进行对比分析,结果表明:接触算法更接近实际受力情况。
非线性接触;索塔锚固区;接触对;等效线荷载
法国教授M.Jacques于1988年提出了Extradosed bridge(超剂量预应力混凝土桥梁)[1],国内学者称为“矮塔斜拉桥”或“部分斜拉桥”[2],其受力特点与连续刚构相似,可以理解为把梁体内的一部分预应力移动到桥塔上,索鞍相当于体外预应力索的转折点[3-4]。国内矮塔斜拉桥近10年才发展起来,已建和在建的超过30座[5]。目前的矮塔斜拉桥索塔锚固区构造大部分为双套管结构,分丝管结构是近几年兴起的,它由集束钢管组焊而成,钢绞线对应穿过每束钢管,具有避免应力集中、易换索等优点,见图1。但是分丝管与索鞍接触处的应力分布较为复杂,国内研究这种新型的分丝管结构对索塔锚固区影响的文献较少,之前计算方法为等效线荷载和等效面荷载。笔者以云南南盘江大桥为依托,基于接触理论采用大型有限元软件对索塔锚固区进行非线性接触分析。
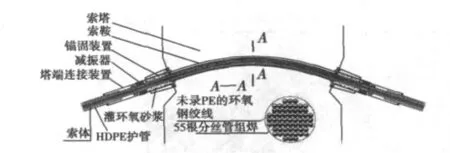
图1 分丝管构造Fig.1 Structure of the strand-separatingtubular-saddle
1 工程概况
云南南盘江大桥是主跨108 m+180 m+108 m矮塔斜拉桥,主梁为单箱3室斜腹板变截面箱梁,根部梁高5.8 m,端部等截面梁高3 m,梁高按2次抛物线变化。主塔采用矩形实心断面,平面尺寸5.5 m×2.6 m,桥面以上塔高29 m,见图2。斜拉索为单索面双排布置在中央分隔带上,全桥4×9对拉索。斜拉索在塔上锚固方式采用钢绞线斜拉索在塔上通过集束钢管贯通(索鞍)锚固方式。主要构造是采用焊接集束分丝钢管。
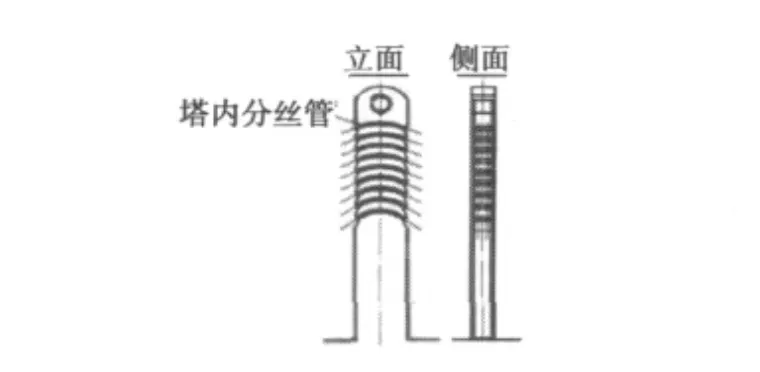
图2 南盘江大桥索塔构造Fig.2 Structure of cable tower
2 等效线荷载分析
2.1 节段模型
为简化计算,取索力最大的第9节段作为计算对象,用有限元软件模拟拉索的等效竖向线荷载(Madis/civil计算的全桥索力见表1),并加载在9号索鞍孔道处,加载图示和计算结果分别见图3和图4。
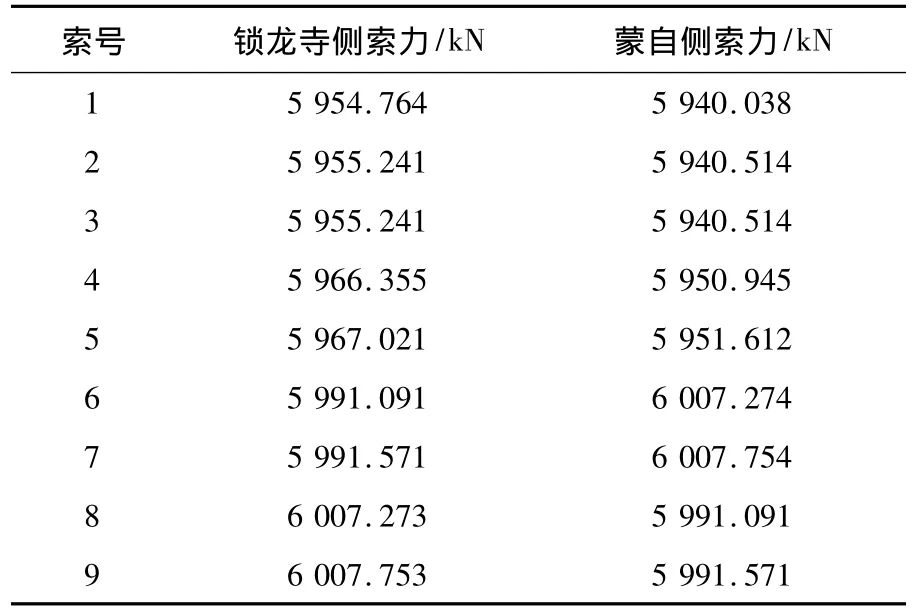
表1 Madis/civil计算的成桥索力Tab.1 Completion value by Madis/civil
2.2 结 论
从图4的主压应力云图看,最大主压应力为12.14 MPa,在设计容许压应力范围内;图5中最大主拉应力为1.03 MPa,也在设计容许拉应力范围内。


图5 主拉应力Fig.5 Principal tensile stress
3 接触理论分析原理
3.1 分析原理
当表面发生接触时,在接触面之间一般传递切向力和法向力,这样在分析中就要考虑阻止表面之间相对滑动的摩擦力。库伦摩擦[6]用来描述接触面之间相互作用的摩擦模型,该模型应用摩擦系数μ来表征在2个表面之间的摩擦行为。在表面拉力达到一个临界剪应力值之前,切向运动一直为0,方程的临界剪应力取决于法向接触压力,即公式τcrit=μp,乘积μp是接触表面间摩擦剪应力的极限值,这里p是两表面间的接触压力。直到接触面间的剪应力等于摩擦剪应力的极限值μp时,接触表面才会滑动(相对滑动)。大多数表面μ的取值通常小于单位1。在图5中,用实线总结了库仑摩擦模型的行为:当它们黏结时(剪应力小于μp),表面间的相对运动(滑移)为0。否则将会产生相对滑移,此时程序自动计算罚刚度(图6虚线的斜率)。文中分析要考虑拉索与鞍座之间摩擦力,就要应用到库伦摩擦模型。
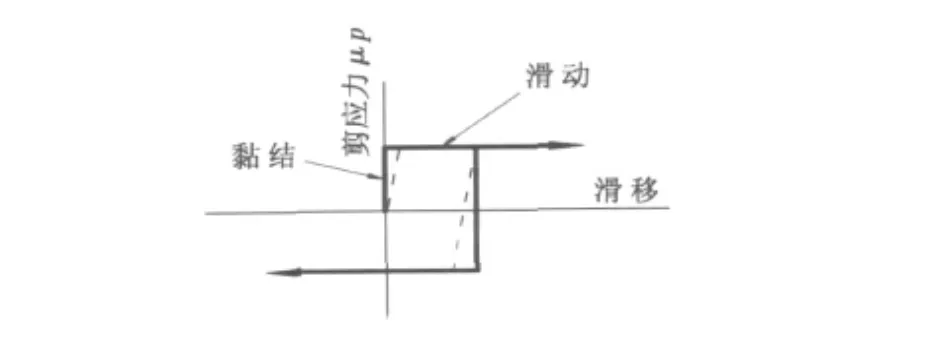
图6 摩擦特性Fig.6 Friction properties
3.2 基本假定
1)为方便计算把55束分丝管等效为一束,直径为 9.8 cm;
2)假定拉索表面与塔直接接触;
3)忽略索塔两侧不平衡索力的影响,直接用Madis civil中计算的最大索力6 007.753 kN加载,转化为拉索应力值为790 MPa;拉索与混凝土之间摩擦系数根据JTG D 62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[7]取值0.3;
4)忽略塔内钢筋影响;
5)节段底部固结固结,顶部自由。
3.3 建 模
采用大型有限元软件对索塔进行静态接触分析[8],取索力最大的9号索节段进行局部分析,混凝土和拉索采用实体单元,用接触对定义拉索与鞍座的接触关系,在定义接触过程中,刚度相对小的面定义为从属接触面,另一面定义为目标面,此模型把拉索视为目标面,鞍座视为从属面,共划分22 633个节点和26 943个单元,见图7。材料特性见表2。

图7 索塔及9号节段网格模型Fig.7 Cable tower segmental grid model

表2 材料特性Tab.2 Material properties
3.4 计算与分析
为了便于观察应力分布情况现取鞍座孔道的剖断面图(图8~图14)。

从图8中看到接触压应力最大值为21.03 MPa,小于混凝土抗压强度设计值fcd值,JTG D 62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[7]中 C55 混凝土 fcd=24.4 MPa。从图 10 应力云图看鞍座顺桥向摩擦剪应力6.28 MPa,由μp=0.3 ×21.03=6.309 MPa,摩擦剪应力极限值大于顺桥向的最大剪应力,所以9号节段拉索与索鞍接触处无相对滑移产生。
图9和图11中鞍座顺桥向接触压应力和剪应力分布规律为应力由鞍座孔道外侧到内侧逐渐增大,峰值的直线段与圆弧段的交界处附近,随后应力逐渐减小。
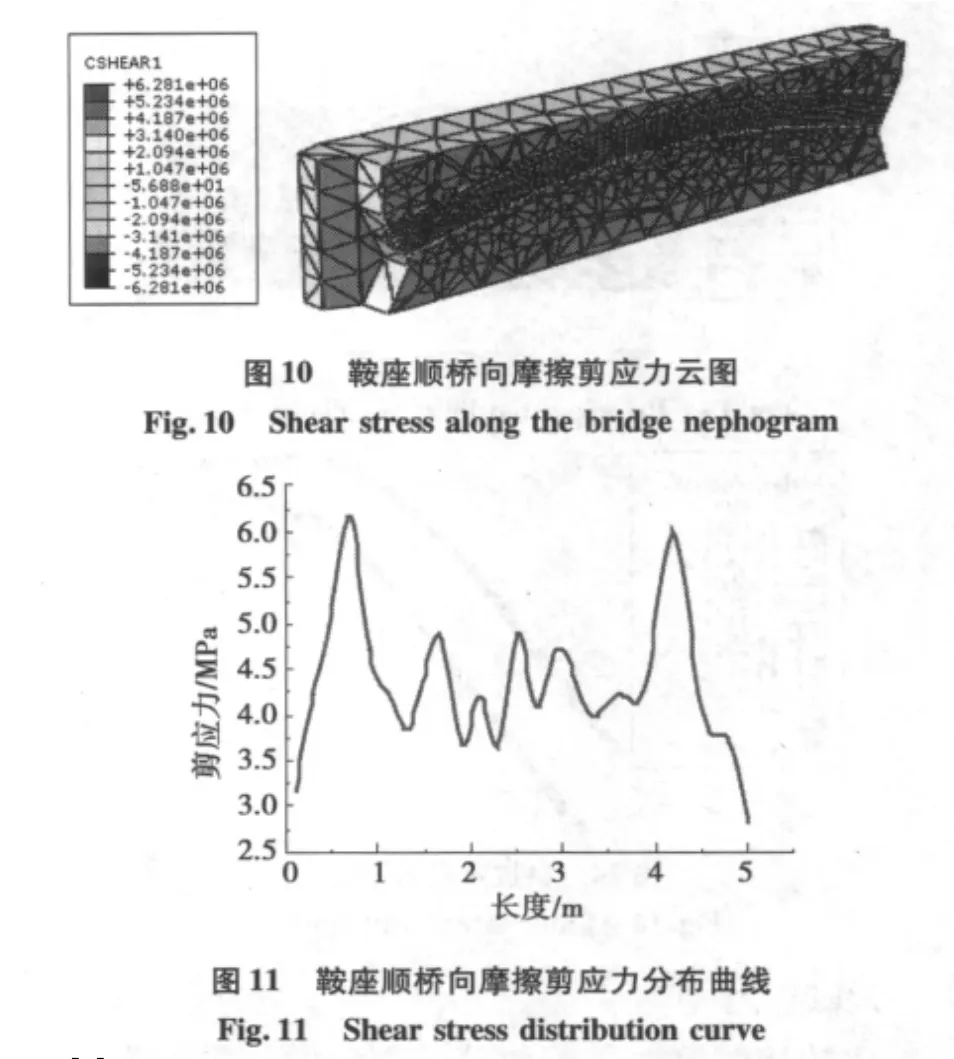

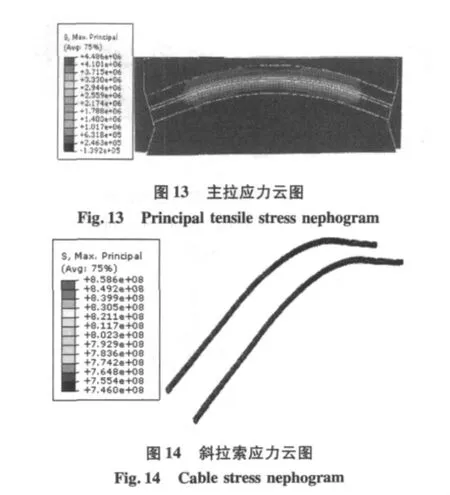
图12 主压应力云图Fig.12 Principal compression nephogram
从图12的计算结果可以看出最大主压应力12.4 MPa,出现在鞍座内直线段与圆弧段交界处,图13中最大主拉应力为4.48 MPa出现在鞍座孔道内圆弧段弧顶处。根据最大拉应力强度理论(第1强度理论)[9]当构件内一点处的最大主拉应力达到材料的极限应力f1时,材料发生脆性断裂。该强度理论适合混凝土、铸铁、岩石等脆性材料。可作为混凝土破坏的简单依据。
从图14看出斜拉索索力是由外到内渐变的趋势,索力值范围为750~860 MPa之间,也在容许范围值之内。
4 对比分析
比较接触算法与等效荷载算法的结果见表3。

表3 应力对比Tab.3 Stress comparison /MPa
通过接触算法与等效线荷载加载结果的对比来看,等效荷载法无法考虑到因摩擦产生的应力集中和拉索对鞍座顶部产生的较大拉应力的影响,由此得出接触算法更接近于实际受力情况。
5 结论
通过对云南南盘江大桥索塔锚固区进行非线性接触分析,得到以下结论。
1)圆弧段半径的大小会影响鞍座下混凝土应力分布,拉索半径越大,混凝土应力分布越均匀。但半径过大拉索与主梁夹角越小,分担竖向荷载较小。所以设计合理的半径对索塔及全桥受力有很重要的影响。
2)应用接触分析理论,模拟了矮塔斜拉桥的拉索表面与混凝土孔道表面的接触问题,与等效线荷载比较,接触分析结果更接近锚固区真实受力情况。
3)接触非线性属于高度非线性,数值分析很难收敛。必须调整能量耗散因子(dissipated energey fraction)精度或修改从属单元调整系数(tolerance for adjustment)才能实现。
4)利用接触理论分析的索鞍处直线段与圆弧线交界处易发生较大压应力,且鞍座内孔道弧顶易产生交大拉应力,建议在这2个位置增加受力钢筋抵抗较大的拉压应力。
5)利用等效原理将55束分丝管模拟为一束,忽略了外钢管的影响,因此不能很好的模拟分丝管中钢绞线的相互作用。如何真实模拟分丝管内的作用将是下一步要研究解决的问题。
[1]Virlogeux M.Recent evolution of cable-stayed bridges[J].Engineering Structures,1999,21(8):737-755.
[2]陈从春,周海智,肖汝诚.矮塔斜拉桥研究新进展[J].世界桥梁,2006(1):70-73.
CHEN Cong-chun,ZHOU Hai-zhi,XIAO Ru-cheng.The research progress of extradosed cable-stayed bridge[J].World Bridges,2006(1):70-73.
[3]李晓莉,肖汝诚.矮塔斜拉桥的力学行为分析与设计实践[J].结构工程师,2008,21(4):7-9.
LI Xiao-li,XIAO Ru-cheng.Mechanical behavior analysis and design experience of low-pylon cable-stayed bridge[J].Structural Engineers,2008,21(4):7-9.
[4] 王伯惠.斜拉桥结构发展和中国经验[M].北京:人民交通出版社,2003.
[5]孙测世,周水兴,童建胜.部分斜拉桥施工控制特点[J].重庆交通大学学报:自然科学版,2010,29(2):177-179.
SUN Ce-shi,ZHOU Shui-xing,TONG Jian-sheng.Discussions on characteristics of construction control for extra-dosed partially cable-stayed bridges[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(2):177-179.
[6]庄茁,由小川,岑松,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.
[7]JTG D 62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.
[8]Hertz H.Uber Die Berubrung Fester Elastischer Korper[J].Journal Fur Die Reine Und angewandte Mathematik,2009,882(92):156-171.
[9] 刘鸿文.材料力学:I[M].北京:高等教育出版社,2004.
Stress Analysis of Anchorge Zone of Cable Tower in Extradosed Cable-stayed Bridge Based on Contact Theory
SONG Jun1,WANG Fu-min2,GENG Bo2,HU Jing2,ZHOU Man1,ZHAO Yan-lei1
(1.School of Civil Engineering& Architecture,Chongqing Jiaotong University,Chongqing 400074,China;
2.Chongqing Communications Research & Design Institute Co.,Ltd.,China Merchants Bureau,Chongqing 400067,China)
A nonlinear contact model for anchorage zone of cable tower with strand-separatingtubular-saddle was established via large-scale finite element software;simulating contact relation between cable and saddle by contact pair was carried out;stress distribution in the concrete on tower wall was discussed as well as transfer and distribution of cable force based on exquisite simulation calculation for the model.Comparative analysis of model through equivalent linear load was conducted.Results indicated that contact algorithm was close to actual level.
nonlinear contact;anchorge zone of cable;contact pair;equivalent linear load
U442.55
A
1674-0696(2011)03-0353-04
2011-01-14;
2011-03-08
宋 军(1982-),男,山东威海人,硕士研究生,主要从事桥梁结构分析方面的研究。E-mail:songjun1982@163.com。

