多孔结构孔隙特征的分形研究

刘 阳,贾俊超,王 磊

(1.中国矿业大学力学与建筑工程学院,江苏徐州221008;2.鄂尔多斯永煤矿业投资有限公司,内蒙古鄂尔多斯017000)

1 孔隙体积分形研究

1.1 海绵体体积分形原理

对于混凝土多孔介质的静态孔隙结构,多采用Menger海绵体模型进行分析,如图1。具体构造过程为：对于一个边长为R的立方体,将边长R分成m等份,从得到的m3个小立方体中随机挖去n个孔隙单元,按照这个规则重复操作k次,则得到的多孔介质体中最小的立方体单元的边长为rk=R/mk,剩余立方体的个数为(m3-n)k,利用盒计数法计算出海绵体的体积分形维数为：

根据体积分形原理,海绵体的固体体积Vs与最小立方体单元的长度rk呈幂次关系,对二者进行双对数变换后的关系式为：

那么,得出海绵体的固体体积VS关于分形维数DV的表达式为：

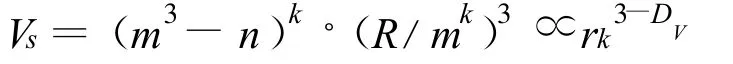
假设海绵体的孔隙率为φ,则得出φ关于体积分形维数DV、边长一次等分数m以及重复挖孔次数k的表达式：

式(2)为孔隙率的分形表达式,该公式用到的孔隙率φk为重复挖孔k次所得到的全部孔隙的累积体积与海绵体的表观体积之比。

图1 Menger海绵体分形模型

依据图1海绵体的构造过程,m=3,在不同迭代次数下,作出孔隙率φk与体积分形维数DV的关系,如图2所示。

图2 孔隙率与孔隙分形的关系

从图2和式2可以看出：孔隙率φR是关于体积分维DV的减函数,多孔结构的体积分形维数越大,孔隙率越低;迭代次数对孔隙率的影响也很大,迭代次数越高,多孔体的最小孔径越小,孔隙率随体积分形的变化越不明显。

1.2 基于压汞实验的体积分形研究

将海绵体分形模型与混凝土试块压汞实验的测试机理对比分析,发现二者存在很大程度的相似性,其中rk对应一定汞压下的孔隙直径;R对应测试试块的最小边长;φk对应一定汞压下所能测得的全部孔隙对应的孔隙率。为了用混凝土的压汞实验过程验证海绵体的孔隙分形理论公式推导的准确性,下面在海绵体的分形理论基础上推导了混凝土基于压汞实验的体积分形的计算公式。

海绵体的固体体积VS用体积分形维数DV表示为：

对式(3)两边分别取对数,得到以下关系式：

由式(4)知,混凝土试块的固体体积Vs和一定汞压下的最小孔径rk的双对数曲线呈线性关系,斜率为3-DV;y轴上的截距为DV◦lnR;DV代表多孔结构体的体积分形维数。

2 孔隙表面分形研究

2.1 孔隙比表面积的简易算法

依托Menger海绵体分形模型,研究多孔结构体的比表面积的分形维数,必须满足以下两个基本假定：

①孔结构的孔隙表面为光滑表面;

②孔隙单元体之间没有公用面。

利用Menger海绵体挖孔规则重复k次操作,得到多孔结构体中最小的立方体单元的边长为rk=R/mk,挖掉的孔隙立方体单元的个数为n,按照上面两条基本假定,可以得出多孔结构体的总的表面积为：

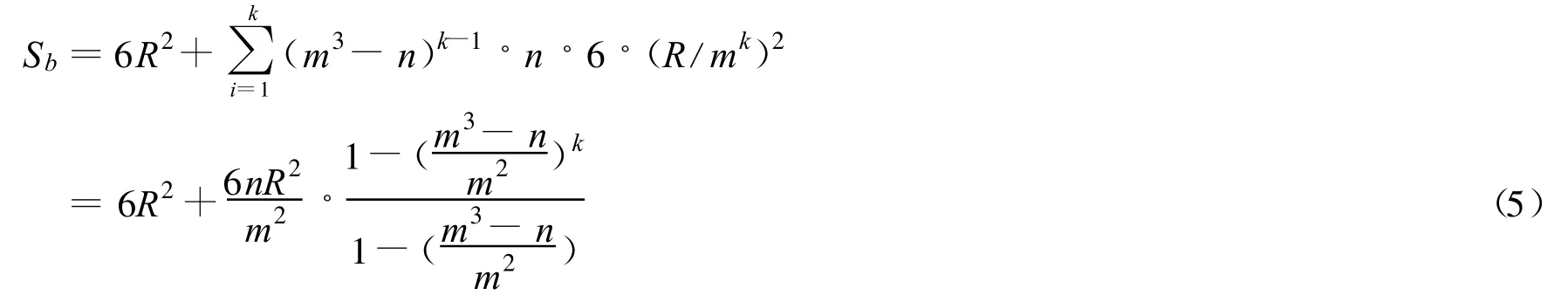
作孔隙体比表面积Ω和孔径rk的双对数曲线,二者呈线性关系,说明孔隙体积比表面积满足分形特征。孔隙体比表面积的分形计算公式为：

由式(7)得知：孔隙体积比表面积Ω是关于DV与rk的函数;多孔结构体的比表面积满足分形特征。由式(2)可以表示为：φk=f(DV,m,k),说明孔隙率仅与体积分维DV一个标度不变量有关。联合式(7)可知：孔隙比表面积Ω仅与孔隙率φk有关。

2.2 基于表面分维的孔隙比表面积算法

本文利用Menger模型推导了多孔结构体比表面积的计算公式(6),限于上述两个基本假定,式(7)导出的孔隙比表面积Ω仅与孔隙率φk有关,而真实的孔隙比表面积除了与孔隙率有关外,还与表面的弯曲粗糙等复杂程度有关,为了更准确的表征多孔体的比表面积,本文对多孔体的孔隙表面分形展开进一步研究。

下面考虑孔隙的表面分形效应,采用增加型分形构造法计算孔隙的比表面积。在一个自相似系统中,经k阶迭代后,第k阶的孔隙表面积与测量尺寸的关系可由下式给出：

式中：ε为测量尺度,无量纲;a为常数;DA2为表面分形维数。

构造第k阶的孔隙的表面积的算式为：

式中：ε为孔隙表面分形的测量尺度,与测量体积分形的测量尺度R/mk相互独立;Sgk为第k阶光滑孔隙表面的面积。

由于孔隙比表面积的测量比较复杂,而且都不够准确,直接利用表面分形原理计算DA2比较麻烦。我们根据DA2=DA1+1的关系,间接求解表面分维数。对多孔体试块剖切,然后电镜扫描断面孔隙情况,用一个变化的测量尺度ε孔隙的圆周,计算孔隙周长的一维分形维数DA1,然后代入DA2=DA1+1,就得到了孔隙的表面分形维数。

沿用前面海绵体分形模型的孔隙构造方法,可知第k阶迭代后生成小立方体孔隙表面个数为：

由式(8)和(9)经过k次迭代后,孔隙的总的表面积的表达式为：

式中Sb为孔隙内表面积,其值远大于外表面积6R2。为了更准确的表征孔隙的粗糙度,下面计算了多孔体的孔隙比表面积。

由式(10)看出：孔隙比表面积是体积分维DV和表面分维DA2两个独立变量的函数,不仅表征了孔隙率和孔径分布情况,还能表征孔隙表面的褶曲粗糙程度。

3 结论

⑴多孔结构的体积分形能够通过压汞实验获得。经过理论推导发现,多孔结构的体积分维是其孔隙率的唯一的标度不变量,因此可以用体积分形来表征多孔结构体的孔隙率的大小。

⑵孔隙率φ是关于体积分维DV的减函数,多孔结构的体积分形维数越大,孔隙率越低;压汞实验后期,随着压汞仪的压力不断提高,渗透性试件的最小孔径越来越小,孔隙率随体积分形的变化越不明显;

⑶描述多孔结构体的几何特征,除了孔隙率和孔径大小外,还要了解孔隙的表面粗糙度。本文基于Menger海绵体模型推导了多孔结构比表面积的计算公式(6)和(10),前者是光滑表面的孔隙比表面积的算法,后者考虑了孔隙表面的弯曲粗糙等复杂程度的影响。

⑷本文给出了孔隙体的几何分形的有关算法,能够清楚地认识多孔结构的复杂结构特征,对于今后开展多孔结构成分的絮凝过程、多孔结构渗流的研究有重要的指导意义。

[1] 唐明.混凝土孔隙分形特征的研究[J].混凝土,2000(8)：3-5.

[2] 杨书燕,姜忻良,李新国.基于分形理论的土体微结构分析[J].中国港湾建设,2005(2)：14-20.

[3] 王学龙,胡锐,薛祥义,等.孔径分布对多孔镍孔体积分形维数的影响[J].材料导报,2009(3)：66-68.

[4] 王清,王剑平.土孔隙的分形几何研究[J].岩土工程学报,2000,22(4)：496-498.

[5] 刘伟,范爱武,黄晓明.多孔介质传热传质理论与应用[M].北京：科学出版社,2006.

[6] 孙霞,吴自勤,黄田匀.分形原理及其应用[M].合肥：中国科学技术大学出版社,2003.

[7] 谢和平.岩土介质的分形孔隙和分形粒子[J].力学进展,2003,23(2)：145-164.

[8] 郑瑛,周英彪,郑楚光.多孔CaO孔隙结构的分形描述[J].华中科技大学学报,2001,29(3)：82-84.

[9] 周宏伟,谢和平.多孔介质孔隙度与比表面积的分形描述[J].西安矿业学院学报,1997,17(2)：97-102.

[10] 尹红宇.混凝土孔结构的分形特征研究[D].西宁：广西大学,2006.