带有临界指数的加权拟线性问题正解的存在性
康东升,沈小凤,杨 芬
(中南民族大学数学与统计学学院,武汉430074)
1 问题的引入
本文研究了下列椭圆方程:
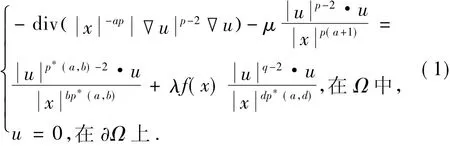
其中Ω⊂RN(N≥3)是包含原点的有界光滑区域,是临界Hardy-Sobolev指数,f(x)是非负连续函数.
在全文中假设:

(H2)f∈C(¯Ω),f(x) ≥0,且在 Ω 中f≠0.
W=W1a,p(Ω,|x|-ap)是C0∞(Ω)关于范数|x|-ap|▽u|pdx)1/p的完备化空间.在W中定义问题(1)的能量泛函为:
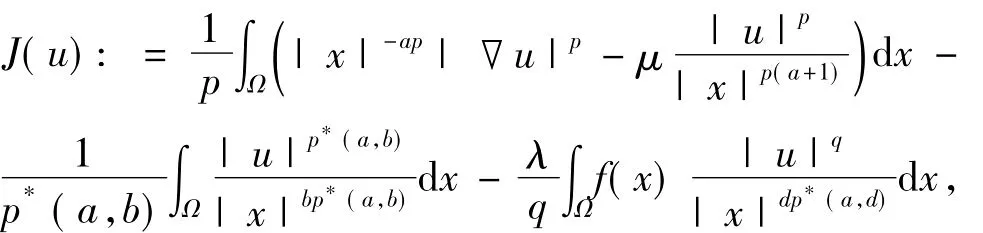
那么J∈C1(W,R),如果对∀v∈W有〈J'(u),v〉=0成立,那么u∈W称为问题(1)的解,即求问题(1)的解就等价于求J的非零临界点.由椭圆正则性理论知u∈C1(Ω{0}).
研究问题 (1)的重要工具是Caffarelli-Kohn-Nirenberg 不等式[1]:
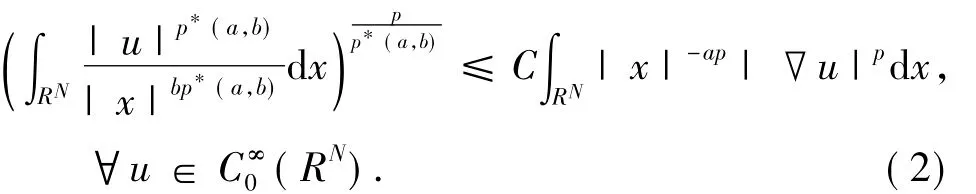
当b=a+1时p*(a,b)=p,上式变为著名的Hardy不等式[1]:
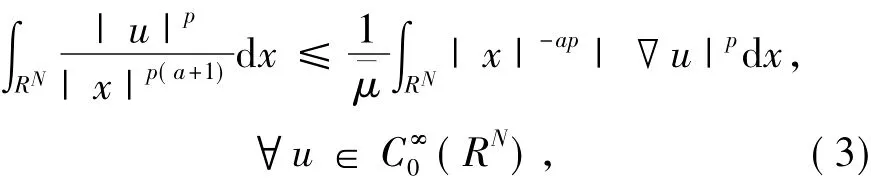
当μ<时,空间W中的范数定义为:
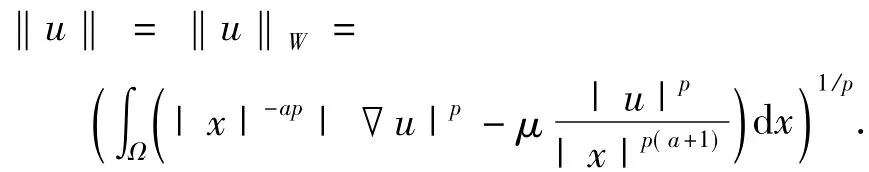
由(2)式和(3)式,当μ<¯μ时,可以定义最佳常数[2,3]:
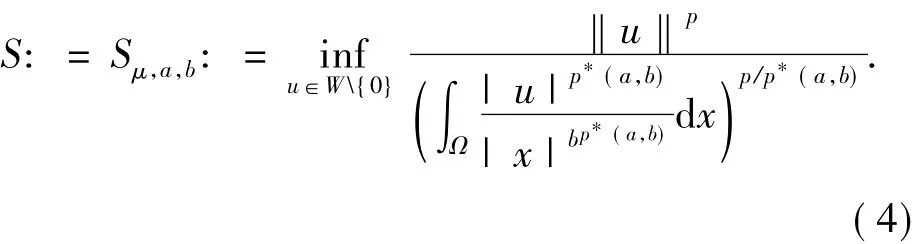
那么S>0.
参照文献[4]作如下定义:
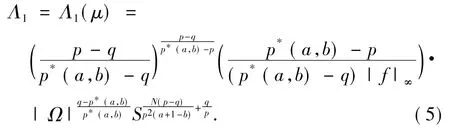
其中|Ω|是Ω的Lebesgue测度.
本文的主要结果可以总结为下面的定理1.
定理1假设(H1)和(H2)成立,则存在λ>0,使得对任意的λ∈(0,Λ1),问题(1)存在一个正解.
在下面的讨论中,我们常常用C来表示正常数,为了简单起见,我们省略掉积分号中的“dx”.
2 预备定理
首先考虑映射:φλ:W→R,满足:

结合问题(1)考虑:
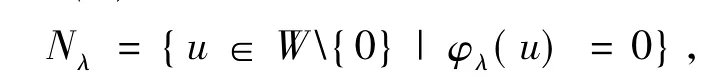
并将Nλ分成3 部分[5]:
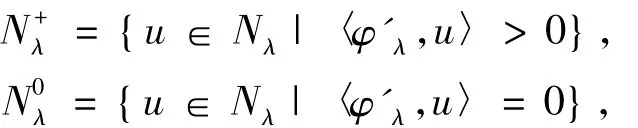

那么Nλ包含问题(1)的所有解,u∈Nλ当且仅当:
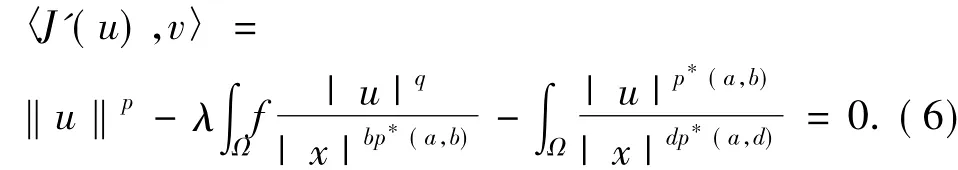
引理1对任意的λ∈(0,Λ1)有Ø.
证明用反证法,假设∃λ0∈(0,Λ1)使得≠ Ø,则N0λ⊂W且当u∈时有:

从而有:
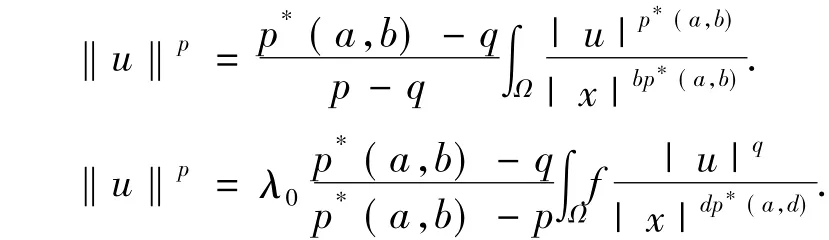
则由Holder不等式及(2)式得:
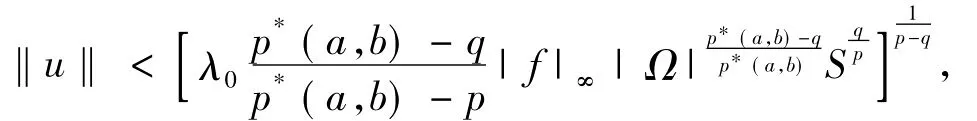
并且,
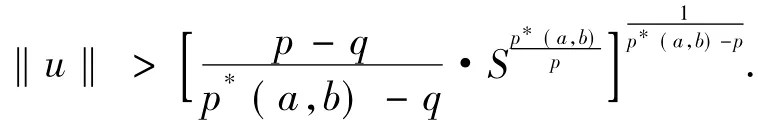
因此就有:

这与λ0∈(0,Λ1)矛盾,从而对任意的λ∈(0,Λ1)有Ø.证毕.
由引理1知,对任意的λ∈(0,Λ1)有Nλ∪,定义:
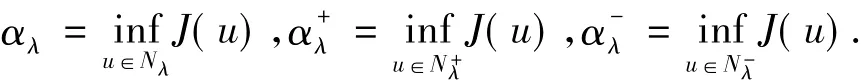
引理2(i)对∀λ∈(0,Λ1)有αλ≤<0.
(ii) 存在依赖于 λ,μ,p,q,N,S,|f|∞和|Ω|的常数d0>0,使得对∀λ∈(0,Λ1)有>d0.
证明(i)令u∈,由(7)式知:
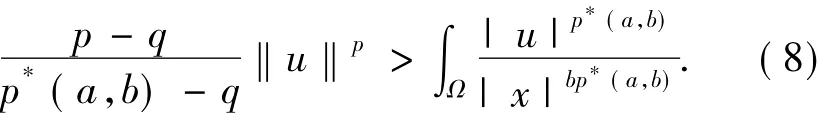
又由(6)式得:
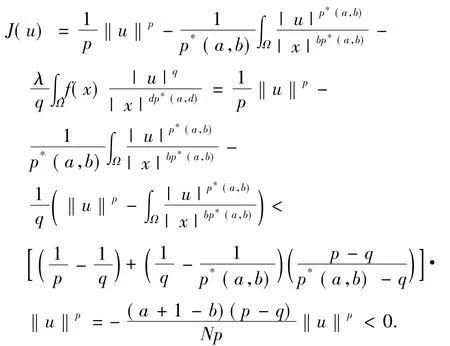
因此,根据αλ和的定义有αλ≤<0.
式知:
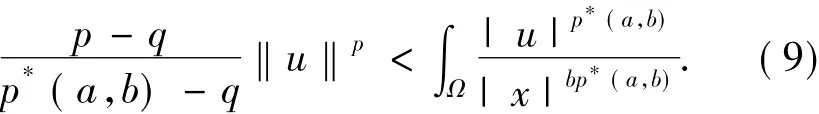
根据S的定义,得到:
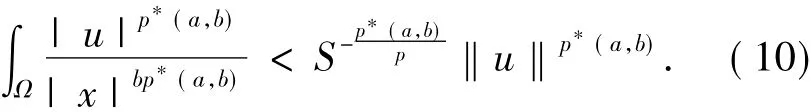
由(9)式和(10)式可以推出:

从而由(7)式及(11)式有:
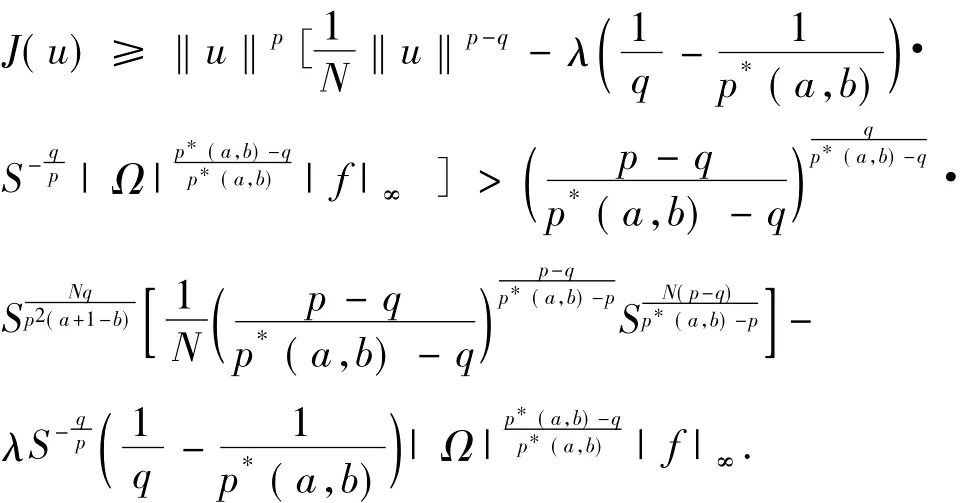
即J(u)>d0,∀u∈,
其中d0=d0(λ,μ,p,q,N,S,|f|∞,|Ω|) 是正常数.证毕.
对任意u∈W使令:
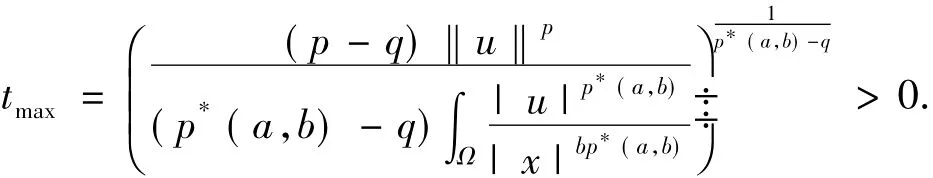
引理3[6]假设λ ∈(0,Λ1),函数u∈W满足
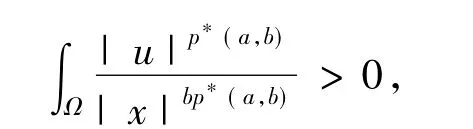
3 定理的证明
引理4 (i)若λ∈(0,Λ1),那么泛函J存在(PS)αλ序列{un} ⊂Nλ.
证明过程可参考文[7].
引理5若 λ∈ (0,Λ1),则J存在极小值点u0∈Nλ+满足:
(i)J(u0)=αλ=.
(ii)u0是问题(1)的一个正解.
(iii)J(u0) →0,当 λ →0+.
证明由引理4(i),对泛函J存在极小化序列{un}⊂Nλ使得:
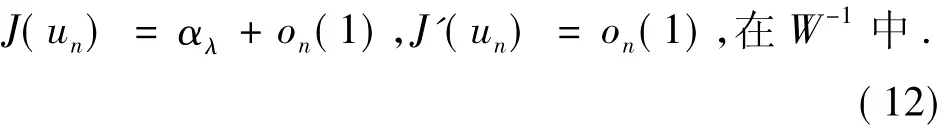
因此序列{un}是有界的,且存在一个子序列(仍记为{un}),从而存在u0∈W使得:
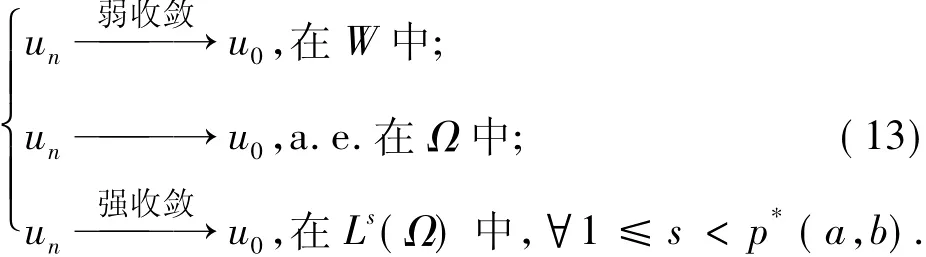
首先,证明u0是问题(1)的一个非平凡解.由(12)式和(13)式易知u0是问题(1)的解,令{un}⊂Nλ,则有:
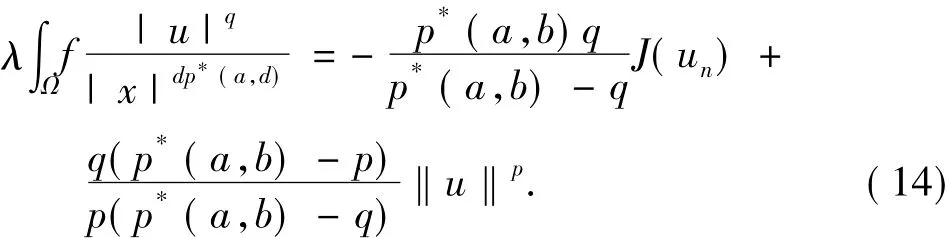
在(14)式中令n→∞,由(12)式和(13)式及αλ<0有:
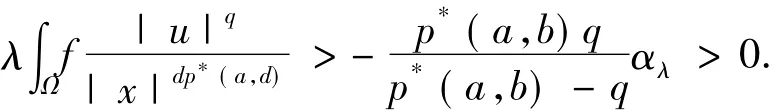
因此,u0∈Nλ是问题(1)的一个非平凡解.
现证明在W中un→u0(强收敛)且J(u0)=αλ.令u0∈Nλ,由 Fatou 引理有:
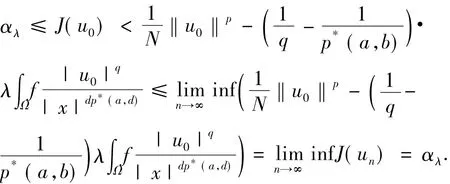
即J(u0)=αλ且.令vn=un-u0,由Brezis-Lieb引理得:
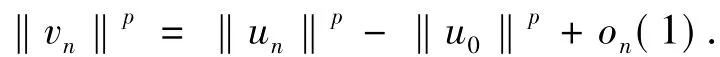
从而在W中un→u0(强收敛),且u0∈.否则,假设u0∈,由引理3(ii),存在唯一的和使得t-u∈和t+u∈.特别地,当1时,
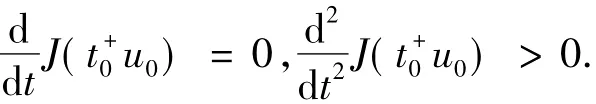
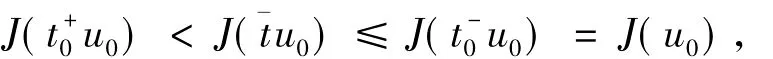
产生矛盾,因此J(u0)=J(|u0|)且|u0|∈N+λ,由引理4知u0是问题(1)的一个非负非平凡解.由强极致原理得u0>0在Ω中,且当λ>0时u0是问题(1)的一个正解.又根据引理2(i)和(7)式得出:<0,
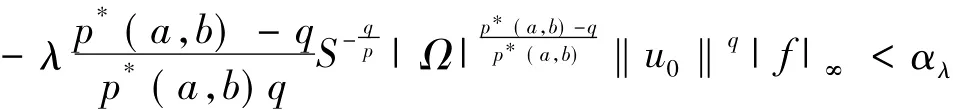
上式意味着J(u0)→0,当λ→0+.
定理1的证明 由引理5知存在λ>0,使得对任意的λ∈(0,Λ1),问题(1)存在一个正解.
[1]Catrina F,Wang Z.On the Caffarelli-Kohn-Nirenberg inequalities:sharp constants,existence(and nonexistence),and symmetry of extermal functions[J].Comm Pure Appl Math,2001,54:229-258.
[2]Kang D.On the quasilinear elliptic problems with critical Sobolev-Hardy exponents and Hardy terms[J].Nonlinear Anal,2008,68:1973-1985.
[3]Kang D.Positive solutions to the weighted critical quasilinear problems[J].Appl Math Comput,2009,213:432-439.
[4]Cao D,Han P.Solutions to criticalelliptic equationswith multi-singular inverse square potentials[J].JDifferential Equations,2006,224:332-372.
[5]Rodrigo da Silva Rodrigues.On elliptic problems involving critical Hardy-Sobolev exponents and sign-changing function[J].Appl Math,2010,73(4):857-880.
[6]Wang L,Wei Q,Kang D.Multiple positive solutions forp-Laplace elliptic equations involving concave-convex nonlinearities and a Hardy-type term[J].Nonlinear Anal,2010,74(2):626-638.
[7]Brezis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents[J].Comm Pure Appl Math,1983,36:437-477.

