代数格上形态算子的表示方法

段 汕，李 琰

(中南民族大学数学与统计学学院，武汉430074)

数学形态学从欧氏空间扩展到完备格是由Serra［1］和 Matheron［2］最早提出的.完备格上形态膨胀与腐蚀运算以偏序关系及确界运算为基础，其表示形式比较抽象.本文以二值形态运算中平移变换的作用为引导，赋予完备格上具备某种特性的交换群，我们称之为代数格，使得完备格的形态运算在表示上具有更明确的结构特征.Heijmans也在文［3］中提出赋予完备格可交换群这一代数结构，但并未给出象二值形态学那样具体的表示.本文基于这一观点，以此为基础研究了这种具有特定代数结构的代数格上形态算子的表示定理，并将这种思想运用于Matheron二值形态算子表示定理与极小内核表示定理的证明.

1 预备知识

所谓完备格，就是一个偏序集L，L的每一个子集都有上下确界.给定两个完备格L和M，把所有L到M的算子的集合记为O(L，M)，O(L，M)是与M具有相同偏序结构的完备格.算子ψ∈O(L，M)有下面的性质:(1)递增的，如果X≤Y，那么ψ(X)≤ψ(Y);(2)格同构，对于X，Y∈L，如果X≤Y，有ψ(X)≤ψ(Y);(3)自同构，在L=M条件下的格同构.算 子 ε ∶L→M如 果 满 足 ε(∧i∈IXi)=∧i∈Iε(Xi)(Xi∈L，i∈I)，ε就是腐蚀;算子δ∶M→L如果满足 δ(∨i∈IYi)=∨i∈Iδ(Yi)(Yi∈M，i∈I)，δ就是膨胀.完备格上形态算子表示定理［4］为:如果ψ(I)=I，格上递增算子ψ就可以表示成对所有腐蚀取上确界的形式;如果ψ(O)=O，ψ就可以表示成对所有膨胀取下确界的形式;其中O是格上最小元素，I是最大元素.下面说明，通过赋予完备格可交换群这一代数结构，格上膨胀和腐蚀算子可以具体表出.

2 代数格上的膨胀和腐蚀

类似于二值形态学中平移变换的作用，假若完备格L上所有自同构构成的群Aut(L)满足交换律公理，则Aut(L)的子群T也是可交换群.如果ψ∈L，τ∈T，ψτ=τψ，ψ 称为T(不变) 算子［4］.当完备格L存在上生成族l，那么对于X∈L，集合l(X)=就是X的上生成族，并且这样就可通过T和l的代数结构来刻划L的代数结构.类似于二值形态学平移群在单点集上的可传递性，子群T在l上是可传递的，需满足2个条件:(1)l的元素在T的作用下仍属于l，∀x∈l，τ∈T，τ(x)∈l;(2)T的算子是自同构，即∀x，y∈l，∃τ∈T，τ(x)=y.

因τ∈T是自同构，l中的元素在T下有一对一的关系:在l中固定一个点o为原点，T中只存在唯一的一个 τx满足 τx(o)=x;这样就有 τx(y)=τxτy(o)，如果 τxτy(o)=o，τy就是 τx的逆 τx－1，y就是x的负元，τy也可标记为τ－x.于是l上的膨胀和腐蚀可以分别用 τ表示为:δy(x)=τy(x)，εy(x)=τy－1(x).因所以.这样用l的元素y来对L的元素X做膨胀和腐蚀就有:

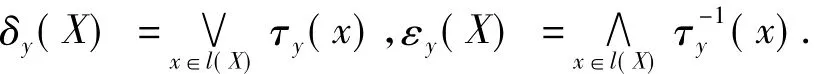
因此，利用T中的变换τ和l的元素可以刻划L的元素，且L上的膨胀和腐蚀具有下面的形式:

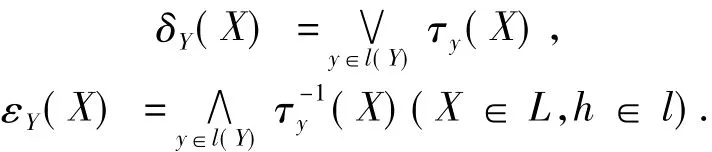
于是在可交换群这一结构下的代数格上的膨胀和腐蚀［5］用τ可以分别表示为:

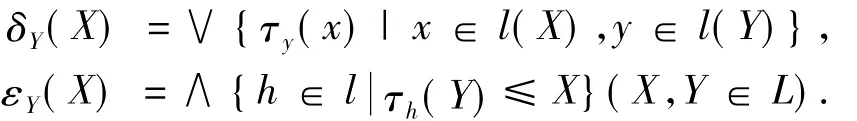
其中l(X)，l(Y)分别是X，Y的上生成族.

3 代数格上的形态算子表示定理

完备格l上的算子ψ的内核定义为V(ψ)={X∈L|ψ(X)≥o}，这里o是l的原点.若ψ(X)≥h(h∈l，X∈L)，将 τ－h作用在其两边，就有 τ－hψ(X)=ψ(τ－h(X)) ≥ τ－h(h)=o，所以 τ－h(X) ∈V(ψ).ψ可重新表示为:ψ(X)=∨ {h∈l|τ－h(X) ∈V(ψ)}，所以重构ψ仅需ψ的内核即可.由此我们可以得出基于τ的T算子表示定理［5］.

1.职责不清。目前公职律师的业务范围基本上与法制机构职责重叠，公职律师与法律顾问、其他税收法制人员之间的关系有待理顺，职责划分、管理架构需进一步明确。

定理1满足条件(1)、(2)的递增T算子ψ可以表示为腐蚀的上确界，即:

证明因ψ是递增的，所以V(ψ)是一个上界集.设X，Y∈L，X≥Y，因Y∈V(ψ)，所以X∈V(ψ).因 εY(X)=∧ {h∈l|τh(Y) ≤X}，o≤εY(X)⇔X∈V(εY).所以取h∈l(ψ(X))，就有ψ(X)≥h，根据前面的分析，X－h∈V(ψ).根据腐蚀和膨胀的定义，δτ－h(X)(h)=δh(τ－h(X))=τh(τ－h(X))=X.根据腐蚀和膨胀的附益性，δτ－h(X)(h)=X⇔h≤ ετ－h(X)(X).因 τ－h(X)∈V(ψ)，τh(Y) ≤X⇔Y≤ τ－h(X)，所 以h≤又因 ψ(X) ≥h，所以.得证.

完备格L上自同构群T满足条件(1)、(2)，其对偶格L'不一定满足该条件，所以T算子ψ不能分解成膨胀的下确界.若l'是L'的下生成族，l'={x∈l'|x≥X，X∈L'}，T'是L'上可交换的自同构群，因此T'要满足:(1')l'的元素在T'的作用下仍属于l'，∀x∈l'，τ ∈T'，τ(x) ∈l';(2')T'的算子是自同构，即∀x，y∈l'，∃τ∈T'，τ(x)=y.对偶自同构v是L的反序双射，若满足v(v(X))=X，即v2=id(这里id是恒等算子)，v就称为负算子.如果v满足vτv∈T(τ∈T)，v就称为L的T相容.这样T算子ψ的对偶算子就定义为ψ*=vψv.用τ来表示定理 1 的扩展［5］，见如下定理 2.

定理2L是满足条件(1)、(2)的完备格，且有一个T相容的负算子，则每一个递增T算子ψ可以写成

其中ˇY=∨{τ－y(o)|y∈l(Y)}.前面已经证明了第1个等式，下面证明第2个等式.

证明根据第1个等式就有.将代入，得到两边同时取负，就有.得证.

假设Y∈V(ψ)且Y⊆X，因此X∈V(ψ)，根据上界集的定义［4］，V(ψ) 是一个上界集.若A，B∈V(ψ)，且A≤B，那么 εA≥ εB，εB(X) 就包含在εA(X)中，这说明定理2的表示存在冗余，为了消除这种冗余，下面引入算子的极小内核元素和基的概念.如果V(ψ)内没有比A更小的元素，元素A是V(ψ)极小内核元素.所有的极小内核元素构成的集合就是ψ的基，标记为Vb(ψ).

如果A是偏序集L的极小元素，那么L中就不存在比A∈L更小的元素.在这种情况下极小内核元素是内核的极小元素.佐恩引理［4］提供极小元素存在的充分条件:如果偏序集L的每一个全序子集都有下界，那么L有极小元素.我们的目的是找到在何种情况下T算子有腐蚀的上确界那样的极小表现.这就等价于:A满足ψ(A)≥o，找到一个极小元素A0≤A使得ψ(A0)≥o.L的全序子集C和算子ψ，若满足ψ(∧C)=∧X∈Cψ(X)，ψ就称为格上半连续的;若满足ψ(∨C)=∨X∈Cψ(X)，ψ就称为格下半连续的［4］.每一个属于格下半连续T算子ψ的内核V(ψ)的A都存在一个极小内核元素A0≤A.这样，T算子表示定理用τ来表示就是如下定理3.

定理3L是满足条件(1)、(2)的完备格，则每一个L上的递增的格上半连续T算子ψ都有一个非空的基Vb(ψ)，且如果L有T相容的负算子，那么每一个递增的格下半连续T算子ψ可表示为:

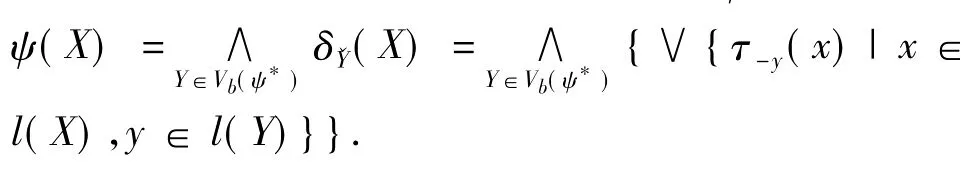
证明根据佐恩引理和前面的结论，递增的格上半连续T算子ψ有非空的基Vb(ψ)，根据定理1的证明显然成立.下面证明第2个等式.因为ψ是格下半连续的，存在链C使得两边取负，得到 ψ*(∨C)所以 ψ*是格上半连续的.根据又因，所以得证.

从上面的讨论中，我们可以看出代数格上的形态算子最终可以有定理3那样的极小表示.下面我们说明，Matheron二值表示定理是其特殊情况，并有定理3那样的极小表示.

4 二值形态算子表示

二值形态学将图像视为一个集合E，E为连续空间Rd或离散空间Zd(d≥1)，幂集P(E)是一个完备格.L=P(E)，T是E上所有可交换平移群，如果E有一个由向量和构成的含有原点o的可交换群集合，单点集就构成P(E)的上生成族l，P(E)上的平移变换算子定义为τa:τa:{x}→{x+a}，其中a∈l(A)=E.Xa是X沿着向量a的平移，这样τa定义P(E)上的一个自同构.对于L就有.因膨胀和腐蚀分别表示为:.我们可以看出二值腐蚀和膨胀是完备格的特殊情况.

根据上面的讨论，P(E)上的自同构τa构成的集合T={τa|a∈E}是可交换群.对任意两个点x，y∈E，存在唯一的τ映射x到y，所以条件(1)、(2)仍然适用，负算子v即为取补运算.用前面的思想来重新证明Matheron二值形态算子表示定理，见定理4.

定理4［6］ψ是P(E)上递增的平移不变算子，则

这里ˇA是A的反射集，ˇA={－a|a∈A}，v(ψ)={A∈E|0∈ψ(A)}.

证明X，A⊆E，εA(X)=XΘA={h∈E|Ah

⊆X}，那么X∈v(εA)⇔0∈XΘA.因Ah⊆X，所以A⊆X，根据内核的定义v(εA)={X|0∈εA(X)}={X|A∈X}.v(ψ)是一个上界集，若A⊆X，A∈v(ψ)，就有 ψ ≥ εA;即下面证明因所以，因此由根据腐蚀和膨胀的附益性，由得到这说明

下面引入P(E)上的极小核元素和基的概念:P(E)上的递增算子ψ，集合A∈v(ψ)称为极小核元素，如果A没有属于v(ψ)的真子集.所有极小核元素A构成的集合就是ψ的基，记作vb(ψ).由此得到P(E)上递增的平移不变算子的极小表示，见定理5.

定理5设ψ是P(E)上一个递增的平移不变算子，并且有非空的基vb(ψ)，那么

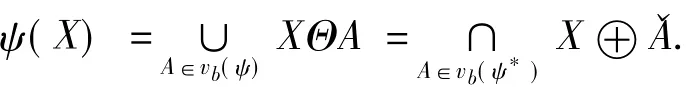
证明设B∈v(ψ)，所以0∈ψ(B)，根据佐恩引理，只要找到一个元素A⊆B，使得A∈v(ψ)，A就是v(ψ)的极小核元素，且A∈vb(ψ).B显然是一个包含零向量的非空集合.若B没有除空集以外的真子集，即B={b}，显然B∈vb(ψ);若B有真子集A，显然A∈v(ψ).所以v(ψ)有极小核元素A∈vb(ψ).根据定理 4第 1个等式的证明显然成立.根据对偶性，得证.

5 结束语

通过本文可以发现，只要改变完备格上变换群的结构，就可以得到相应的形态算子表示.变换群的结构又依赖于τ的结构，因此最终形态算子表示依赖于τ的选择.本文的工作对研究其他代数结构下的形态算子表示以及灰度数学形态学下的算子表示有一定的参考价值.

［1］Serra J.Image analysis and mathematical morphology［M］.London:Academic Press，1988.

［2］Matheron G.Random sets and integral geometry［M］.New York:John Wiley，1975.

［3］Heijmans H.Mathematicalmorphology:an algebraic approach ［J］.CWINewsletter，1987(14):7-27.

［4］Heijmans H.Morphological image operators［M］.Boston:Academic Press，1994.

［5］Heijmans H，Ronse C.The algebraic basis ofmathematicalmorphology，part1:dilations and erosions［J］.IEEE Transactions on Circuits，Systems and Signal Processing，1990，50(3):245-295.

［6］崔 屹.图像处理与分析——数学形态学方法及应用［M］.北京:科学出版社，2000.