静息态人脑功能网络的小世界特性

黄文涛，冯又层

(1中南民族大学电子信息工程学院，武汉430074;2中南民族大学武汉神经科学和神经工程研究所，武汉430074)

人脑约有1000亿个神经元，是一个开放的自组织的复杂巨系统，功能分化与功能整合是其两大基本组织原则［1］.人们一直采用如脑电图(EEG)、脑磁图(MEG)和功能磁共振成像(fMRI)等非侵入式探测手段来观测人脑在任务或静息下的信号，探索人脑的结构和功能组织模式，特别期望能服务于客观准确的对一些“连接失调”脑神经精神疾病［2］(如阿尔兹海默病、癫痫以及精神分裂症等)进行早期诊断、预防和药物治疗评估.一方面随着技术的进步，特别是3T(特斯拉)_的普及，甚至是7T甚高场fMRI的推出，其空间分辨率得到提高，时间分辨率也得到极大改善;另一方面随着静息状态脑功能研究的很多优点逐步被人们认识到(不需要丰富的先验性知识以便去验证某个假设;能探索消耗所谓“暗”能量的脑自发性神经活动［3］;方便对一些特殊人群进行数据采样等)，利用Ogawa等人开创的血氧水平依赖的fMRI技术来探索静息状态下的人脑功能网络成为目前的研究热点［4］，以致人们提出了“功能连接组学”［5］.

目前以探索节点和边的拓扑关系的复杂网络(complex networks)理论已经成为一门横跨多个研究领域的新的科学［6-10］，在生物医学领域得到广泛的应用［11，12］，具体在脑结构、功能和效用网络的探索上取得了初步的成果［13，14］.脑功能网络描述空间上分离的脑皮层各节点之间的时间统计性相关，目前为简单起见一般被看成为无向网络.1998年，Watts和Strogatz发现许多实际网络具有小世界网络特性［15］.本文将对健康正常人的静息态fMRI脑功能连接数据进行复杂网络建模分析，探索其是否具有小世界特性.

1 材料和方法

本研究采用fMRI实验数据［16］，数据预处理采用 SPM2(http://www.fil.ion.ucl.ac.uk/)软件包完成.提取90个脑区的时间序列，采用Achard等人的方法进行最大重叠离散小波变换［17］，针对低频进行相关性分析.以脑区作为节点，脑区功能相关性作为边，设定阈值构建无向简单图.其中要注意的是如果阈值设定太高，图变得非连通;如果设定太低，连通密度过大，与连通花费保守相违背.因为至今没有金标准，这里根据经验进行设定并满足平均度大于节点数的自然对数.计算在 R(http://www.rproject.org/) 和 Matlab(http://www.mathworks.com)平台上进行，利用 Pajek(http://vlado.fm f.unilj.si/pub/networks/pajek/)作图.

2 结果与分析

在脑功能网络关联矩阵的基础上，选择阈值满足图连通，即任何节点的最小度不小于1.这里将阈值设定为R=0.3，得到1146条边连接，即连接密度为0.286的邻接矩阵，如图1，后面的分析在此基础上进行.

图1 脑功能网络邻接矩阵图Fig.1 Map of adjacencymatrix of brain functional network Each element of themap is either white(if there is significant correlation between brain regions)or black(if there is not)

2.1 复杂网络统计量

网络的平均度＜k＞为25.47，小于节点数N=90，但大于节点数N的自然对数(ln(90)=4.50).计算得到静息态脑功能网络的统计量如表1所示.为了进行比较，编写程序代码构建节点数和边数相同的规则网络和随机网络，各网络统计量如表1，显然脑功能网络具有规则网络的大聚集系数又具有随机网络的小特征路径长度.各网络参量比率为 γ=C/Crandom=2.201，λ=L/Lrandom=1.139，则小世界性参量值为σ=γ/λ=1.932.可以看出，γ＞1，λ≈1，σ＞1，即以上参数与小世界理论期望的结果相吻合.

表1 静息态下脑功能网络的统计参量Tab.1 Statistical parameters of the resting state brain functional networks

人们已采用复杂网络的分析方法对基于fMRI［18］、EEG［19］和 MEG［20］等手段采集的有关阿尔兹海默病的病例对照脑功能网络数据进行分析后发现:与对照相比，病例表现失去小世界特性，存在易受损的网络中心(hubs).对帕金森病［21］和精神分裂症［22］等疾病做的脑功能网络研究也得出类似的结论.综合以上研究，静息态下的人脑功能网络具有小世界特性，暗示少量的长程连接既有利于脑神经连接的局部功能分化和连接成本约束，又有利于不同脑功能区之间正常长距信息传输和整合.人脑由健康转变为疾病状态可能是由于脑神经连接的高度局部整合性和完整性遭到破坏，以至于不同脑功能区之间正常长距信息传输和整合遭受阻碍，最终造成“连接失调”脑神经精神疾病的发展和形成［2］.

2.2 度拟合

为了便于直观的观察和分析度分布，作脑功能网络连接图2.同时作双对数图，并按指数分布、幂律分布和指数截断幂律分布进行拟合，如图3.从图可以看出度分布图表现一定的异质性(图2)，存在重尾特性(图3)，但是并没有如幂律分布的异质性那么明显.

图2 脑功能网络连接图Fig.2 Connection graph of brain functional network

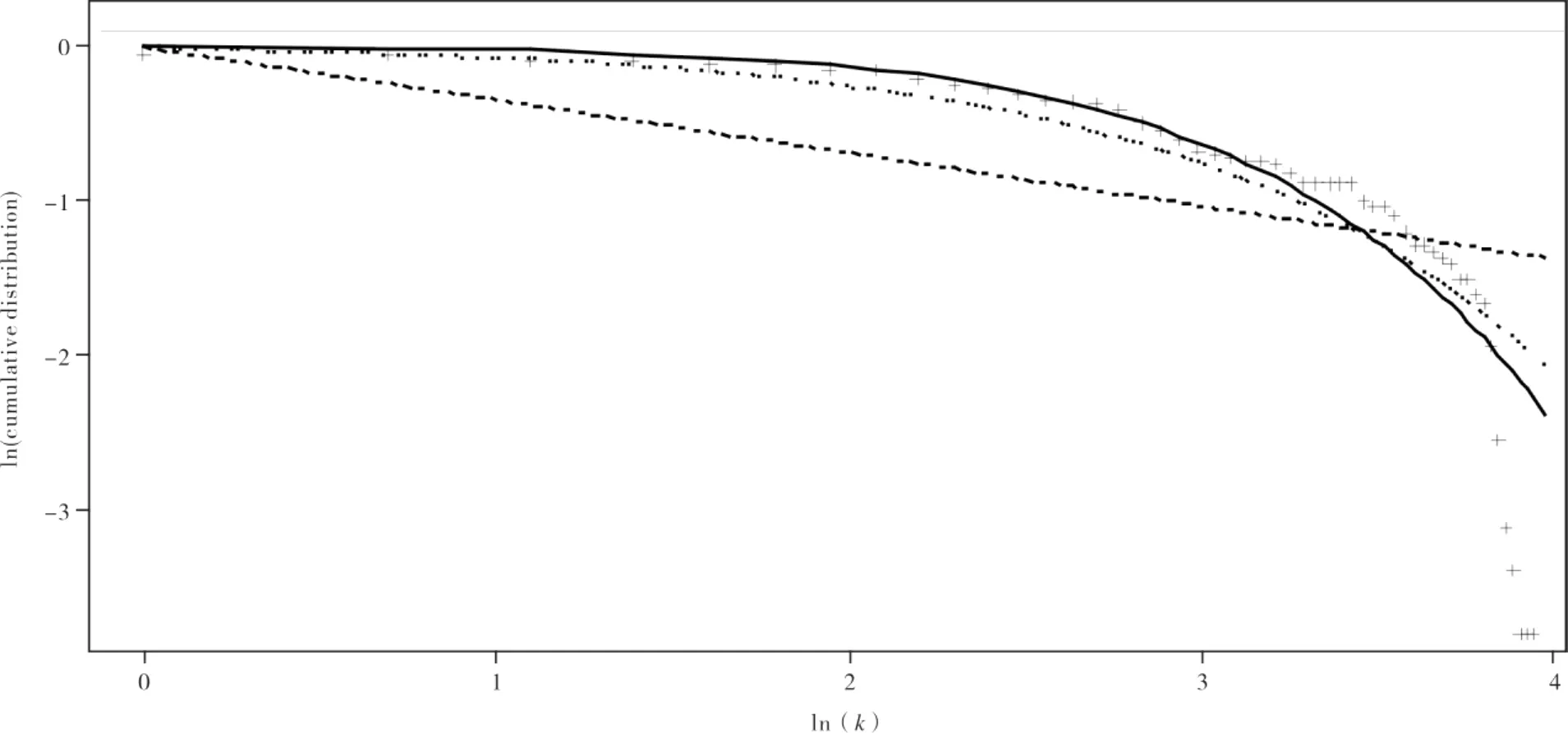
图3 静息态下脑功能网络的双对数度分布图.度的累计概率分布对数对度的对数进行作图，加号表示观测数据，点线是指数拟合，短划线是幂律拟合，实线是拟合最好的指数截断幂律分布Fig.3 Double log degree distribution of the resting state brain functional networks.Plot of the log of the cumulative probability of degree，ln P(ki)，versus lot of degree，ln(ki).The plus sign means observed data，the dotted line is an exponential，the dashed line is a power law，and the solid line is the best-fitting exponentially truncated power law

在体素的基础上进行脑功能网络拟合后，Eguluz等人发现网络度分布服从幂律分布，即具有所谓的无标度特性［23］.复杂网络的无标度特性是Barabasi和Albert提出来的，他们发现实际网络中大部分节点具有很小的度，但是有一小部分节点具有极高的度，即所谓的“富者愈富”现象［24］.这里与前人结果上的差异可能是由于从不同层次上选择节点所造成的.Zalesky等人的研究表明网络拓扑结构的比较应该在相同规模上进行［25］.

3 结语

利用静息态下的人脑fMRI影像数据构建脑功能网络，利用复杂网络理论进行分析.结果显示，静息态下的人脑功能网络具有小世界特性，表明少量的长程连接既有利于脑神经连接的局部功能分化和连接成本约束，又有利于不同脑功能区之间正常长距信息传输和整合.

［1］蒋田仔，刘 勇，李永辉.脑网络:从脑结构到脑功能［J］.生命科学，2009，21(2):181-188.

［2］Delbeuck X，Van der Linden M，Collette F.Alzheimer's disease as a disconnection syndrome［J］.Neuropsychol Rev，2003，13(2):79-92.

［3］Zhang D，Raichle M E.Disease and the brain's dark energy［J］.Nat Rev Neurol，2010，6(1):15-28.

［4］Reijneveld JC，Ponten SC，Berendse H W，et al.The application of graph theoretical analysis to complex networks in the brain［J］.Clin Neurophysiol，2007，118(11):2317-2331.

［5］Biswal B B，Mennes M，Zuo X N，et al.Toward discovery science ofhuman brain function［J］.Proc Natl Acad Sci USA，2010，107(10):4734-4739.

［6］Albert R，Barabási A L.Statisticalmechanics of complex networks［J］.Rev Mod Phy，2002，74:47-97.

［7］Newman M E J.Complex networks:Structure and dynamics［J］.SIAM Review，2003，5:167-256.

［8］Boccaletti S，Latora V，Moreno Y，et al.Complex Networks:Structure and dynamics［J］.Phys Rep，2006，424:175-308.

［9］Costa L D F，Rodrigues F A，Travieso G，et al.Characterization of complex networks: A survey of measurements［J］.Adv Phys，2007，56:167-242.

［10］方锦清，汪小帆，郑志刚，等.一门崭新的交叉科学:网络科学(上篇)［J］.物理学进展，2007，27(3):239-343.

［11］Barabási A L，Oltvai Z N.Network biology:understanding the cell's functional organization［J］.Nat Rev Genet，2004，5(2):101-113.

［12］Mason O，Verwoerd M.Graph theory and networks in Biology［J］.IET Syst Biol，2007，1(2):89-119.

［13］Bullmore E，Sporns O.Complex brain networks:graph theoretical analysis of structural and functional systems［J］.Nat Rev Neurosci，2009，10(3):186-198.

［14］He Y，Evans A.Graph theoretical modeling of brain connectivity［J］.Curr Opin Neurol，2009，23(4):341-350.

［15］Watts D J，Strogatz SH.Collective dynamics of″smallworld″networks［J］.Nature，1998，393(6684):440-442.

［16］Salvador R，Suckling J，Schwarzbauer C，et al.Undirected graphs of frequency-dependent functional connectivity in whole brain networks［J］.Philos Trans R Soc Lond B Biol Sci，2005，360(1457):937-946.

［17］Achard S，Salvador R，Whitcher B，et al.A resilient，low-frequency，small-world human brain functional network with highly connected association cortical hubs［J］.JNeurosci，2006，26(1):63-72.

［18］Supekar K，Menon V，Rubin D，etal.Network analysis of intrinsic functional brain connectivity in Alzheimer's disease［J］.PloSComput Biol，2008，4(6):e1000100.

［19］Stam C J，Jones B F，Nolte G，et al.Small-world networks and functional connectivity in Alzheimer's disease［J］.Cereb Cortex，2007，17(1):92-99.

［20］Stam C J，de Haan W，Daffertshofer A，et al.Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer's disease［J］.Brain，2009，132(Pt1):213-224.

［21］Stoffers D，Bosboom JL，Deijen JB，et al.Are brain networks changed in Parkinson's disease?A graph theoretical analysis of resting-state magnetoencephalographic functional connectivity ［J］.Parkinsonism Relat D，2007，13:S35.

［22］Liu Y，Liang M，Zhou Y，e tal.Disrupted small-world networks in schizophrenia［J］.Brain，2008，131(Pt4):945-961.

［23］Eguíluz V M，Chialvo D R，Cecchi G A，et al.Scalefree brain functional networks［J］.Phys Rev Lett，2005，94(1):018102.

［24］Barabasi A L，Albert R.Emergence of scaling in random networks［J］.Science，1999，286(5439):509-512.

［25］Zalesky A，Fornito A，Harding IH，et al.Whole-brain anatomical networks:does the choice of nodes matter［J］.Neuroimage，2010，50(3):970-983.