乙二醇单醚在超临界二氧化碳中溶解度的研究及关联

杨海健，张 宁，金 晶，张 宇，向 力，李欢欢

(中南民族大学化学与材料科学学院，武汉430074)

超临界流体技术在食品、制药、生物化学、环境治理以及高分子科学等领域有着广泛的用途［1，2］，同时成为绿色友好化学中发展十分迅速的领域.超临界流体将逐渐取代传统的有机溶剂，成为良好的反应介质和萃取剂［3，4］，而超临界 CO2价格低廉，来源广易获取，化学性质不活泼，无毒且不会产生二次污染［5-7］，因此具有广阔的理论研究和实际应用前景.其中，物质在超临界CO2中的溶解度是研究超临界体系的重要物化性质，因此采用有效的测试方法准确测取该溶解度是研究和应用超临界技术的重点准备工作.此外，偏摩尔体积是计算溶质在超临界体系中溶解度的重要参数，准确计算出偏摩尔体积将有助于溶质在超临界体系的其他相关研究.

乙二醇单醚含有亲CO2的醚键、烷基等基团，理论上在超临界CO2中具有良好的溶解性能，可用于香料、油脂及重金属离子的萃取，有望成为创新有效的萃取剂，但其在超临界CO2中的溶解度尚未见报到，且其偏摩尔体积的相关计算至今也未见报道.本文采用静态法，在温度313～363 K，压力 8.2～18.3 MPa条件下，测试乙二醇单甲醚、乙二醇单丁醚在超临界二氧化碳中的溶解度;利用2种半经验公式Bartle和Chrastil对溶解度进行了计算和关联［8-10］;根据 Kumar and Johnston 理论，计算出乙二醇单甲醚和乙二醇单丁醚的在不同温度下的偏摩尔体积.IUPAC国际热力学数据查取溶解压力和溶解温度对应的二氧化碳密度值［12］，计算可知待测物质在超临界CO2中的摩尔分数x.

1 实验部分

1.1 试剂与仪器

乙二醇单甲醚、乙二醇单丁醚购自Acros Chem.公司;高纯 CO2(纯度达99.99%)购自武汉钢铁公司.

PU-1580-CO2CO2Delicery PumP(0～35 MPa)、BP-1580-81 Back Pressure Regulateor、BP-1580-81 Bass Pressure Regulateor购自日本分光公司;不锈钢高压可视反应釜(体积7.11 mL);DF-101B集热恒温加热磁力搅拌器;THYS-15型超级恒温水浴槽.

1.2 溶解度测试

测定溶解度装置见图1.将已知质量的化合物加入到高压可视釜中，缓慢加入CO2驱除釜中空气后密闭体系，开启已设定好温度的恒温水浴和磁力搅拌器，达到热平衡.用注射泵将CO2注入到可视釜中至某一压力时，停止搅拌进行观察，并维持此压力约10 min，如没完全溶解，继续缓慢升高压力直至体系变得均匀透明为止，记录此时的压力，视为溶解压力［11］.每一溶解数据测定3次，取平均值.由

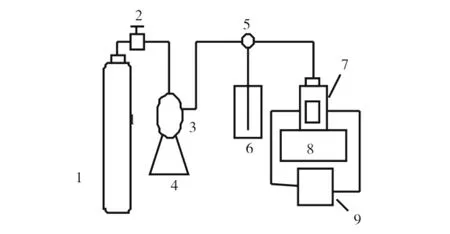
图1 溶解度测试装置图Fig.1 Schematic diagram of the experimental apparatus for solubility tests in supercritical CO2

2 结果与讨论

2.1 溶解度的测试

乙二醇单甲醚和乙二醇单丁醚的溶解度测试条件:温度分别为 313，323，333，343，353，363 K;测试压力8.2～18.3 MPa.根据2种化合物在超临界CO2中的溶解度数据，以实验测得的超临界CO2压力P为横坐标，化合物在超临界CO2中的摩尔分数x为纵坐标作图，得到溶解度-压力关系曲线(见图2和图3).

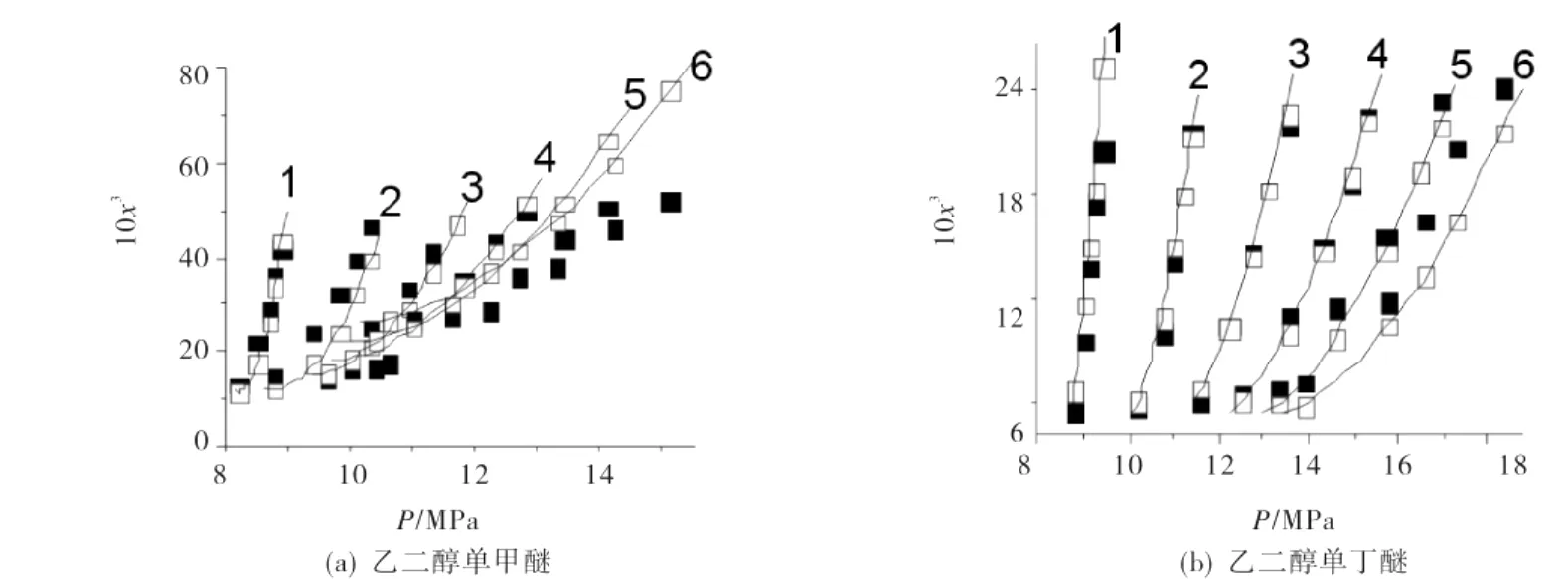
图2 在超临界CO2中2种化合物溶解度实验值与理论值的比较Fig.2 Comparison of solubility experimental and calculated values for the compounds in supercritical CO2

由图2可见，同温下，2种物质的溶解度均随压力的增加而增加，这是因为升高压力可使超临界CO2密度增加，其溶剂化作用增强;同压下，2种物质的溶解度随温度的升高而降低，这是因为温度升高可使超临界CO2的密度减小，溶解能力减弱.同时可见，2种乙二醇单醚物质在超临界CO2中均具有良好的溶解性.其中，当363 K、15.1MPa时，乙二醇单甲醚在超临界CO2中溶解的摩尔分数高达5.2%，这是由于乙二醇单醚中含有亲CO2的烃基和醚键等基团.由图3可见，在超临界CO2中乙二醇单甲醚的溶解性优于乙二醇单丁醚，这是因为同温同压条件下，物质在超临界CO2中的溶解度随烷基碳链的增加而减小所致.

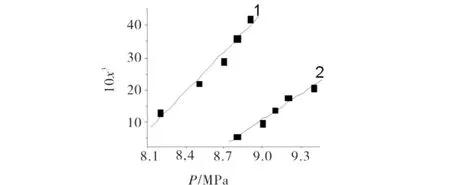
图3 313K时，2种物质在超临界CO2中溶解度的比较Fig.3 Solubility comparison of the compounds in supercritical CO2 at313 K

2.2 Bartle模型的计算与关联

Bartle等［13］提出了利用超临界CO2密度计算和关联物质在超临界CO2中溶解度的半经验公式(1).

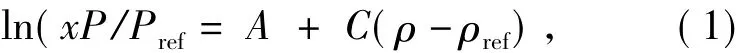
其中:A=a+b/T，即可得式(2).

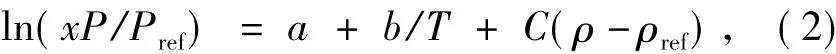
其中，x为溶质的摩尔分数(化合物的摩尔数与CO2摩尔数之比);P为实验测得的CO2的溶解压力;Pref为0.1 MPa; ρ为纯 CO2的密度［12］; ρref为 700 kg/m3;A，C，a，b为常数.第1 步，以 ln(xP/Pref)对(ρρref)作图，经线性拟合得到6条直线(见图4)，其中C值为6条直线斜率的平均值，A为每条直线的截距;第2步，由A对1/T作图(见图5)，经线性拟合得到直线，由该直线可知其截距a和斜率b，2种化合物的a，b，C值见表1.将a、b和C值代入公式(2)中，计算各温度和各压力下的x值，将实验值与理论值进行比较(见图2).

图4 由公式(1)所得2种化合物在不同温度下的ln(xP/Pref)对(ρ－ρref)图Fig.4 Plots of ln(xP/Pref)对(ρ－ρref)，for the compounds at various temperatures

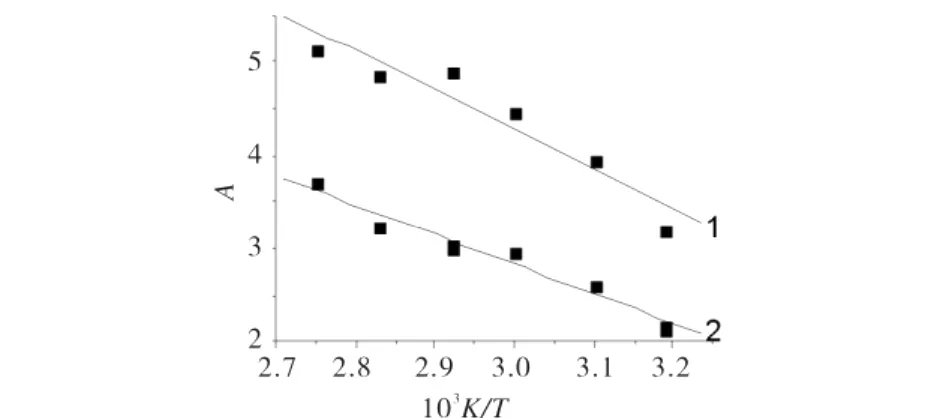
图5 2种化合物A对1/T图;Fig.5 Plots of A vs 1/T for compounds

通过Bartle模型对2种化合物溶解度进行计算与关联，其实验值与理论值的平均相对偏差见表1，分别为16.72%和8.88%，此较小平均相对偏差值表明2种化合物溶解度的实验值能够较好地与理论值吻合，该2种化合物溶解度值具有较高的准确性.

2.3 Chrastil模`的关联与计算

Chrastil模型的关联式见式(3).

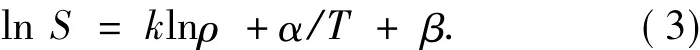
由式(3)计算可得溶解度S.

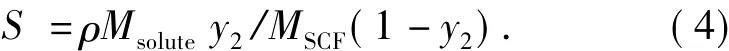
式(3)和(4)中，ρ为纯 CO2的密度［12，14］;S为溶质在超临界CO2流体相中的溶解度;T为实验测试绝对温度;Msolute为溶质的摩尔质量;MSCF为CO2的摩尔质量;y2为溶质的摩尔分数;k，α和β为常数;以lnS对lnρ作图，得到超临界CO2密度与溶解度关系图(见图6);以lnS为因变量，lnρ和1/T为自变量经多元线性拟合可得k，α和β值，2种化合物的诸参数见表2;将k，α和β值代入式(4)，计算各温度和各压力下的S值.

利用公式 AARD=1/n∑︱(Si.cal－Si.exp)/Si.exp︱×100%，计算溶解度的实验值与理论值之间的相对偏差.

表1 由Bartle模型拟合得到2种化合物的溶解度常数及平均相对偏差值Tab.1 Results of the correlation of the solubility data for compounds using the Bartlemodel

通过Chrastil模型对2种化合物溶解度进行计算与关联，所得溶解度常数及实验值与理论值的平均相对偏差值分别为6.00%和7.84%(见表2)，说明溶解度的实验值能够较好地符合理论值，该溶解度结果具有较高的准确性.

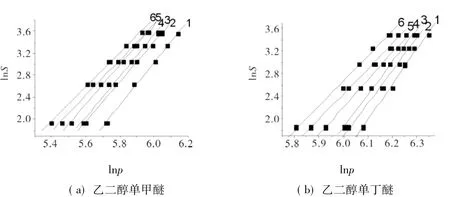
图6 2种化合物在不同温度下的ln S对lnρ图Fig.6 Plots of ln S vs lnρfor the two compounds at various temperatures

表2 由Chrastil模型拟合得到2种化合物的溶解度常数及平均相对偏差值Tab.2 Results of the correlation of the solubility data for compounds using the Chrastilmodel

2.4 溶质偏摩尔体积的计算

根据Kumar and Johnston理论［15］，临界点附近溶质在体系中的溶解度x与其偏摩尔体积之间存在式(5)关系.

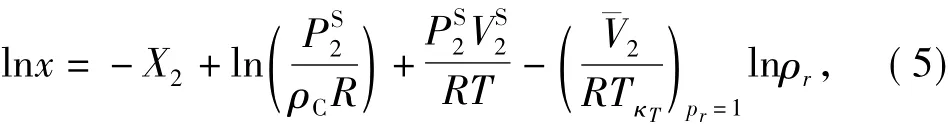
其中，x为溶质在超临界体系中的平衡摩尔分数;PS2、VS2分别为固体溶质的蒸汽压和摩尔体积;R为理想气体常数;¯V2为溶质在超临界点的偏摩尔体积;κT为等温压缩系数(κT= ［(1/ρ)(∂ρ/∂P)T，x］)，ρr为超临界体系的相对密度(ρr=ρ/ρc);T为超临界体系的绝对温度.

当体系在超临界点附近时，溶质的偏摩尔体积¯V2较其摩尔体积VS2大得多，因此式(5)中前3项可视为常数，即可写为式(6).

式(6)中，当0.5 ≤ ρr≤ 2.0 时，溶质在超临界点附近的摩尔分数的对数与相对密度的对数成线性变化关系，其直线的斜率即为溶质在超临界点的偏摩尔体积与流体相等温压缩系数的比值，该比值与ρr无关，已知等温压缩系数κT以及各温度所对应lnx与lnρr的斜率值，即可算得不同温度下物质在超临界点的偏摩尔体积¯V2.

图7为乙二醇单甲醚和乙二醇单丁醚在不同温度下的lnx对lnρr图.由图7可见，lnx与lnρr呈线性变化关系，通过最小二乘法可拟合出对应不同温度下的6条直线，可知每条直线的斜率和线性相关系数σ2;由式(6)斜率、等温压缩系数及对应温度即可求得不同温度下2种化合物在超临界点偏摩尔体积(见表3).

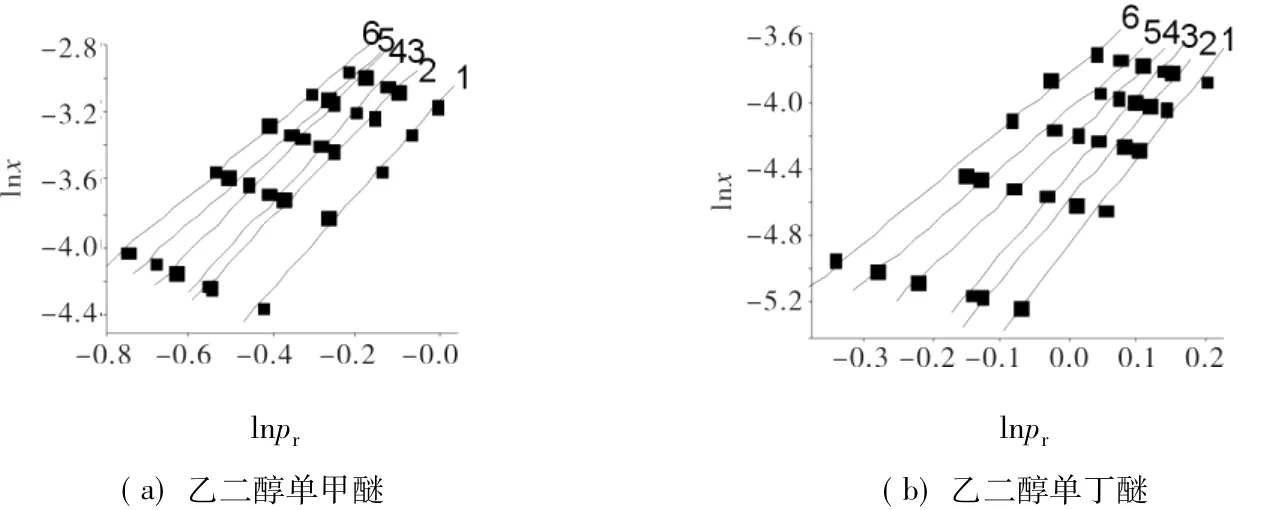
图7 2种化合物在不同温度下的ln x对lnρr图Fig.7 Plots of ln x vs lnρr for the compounds at various temperatures

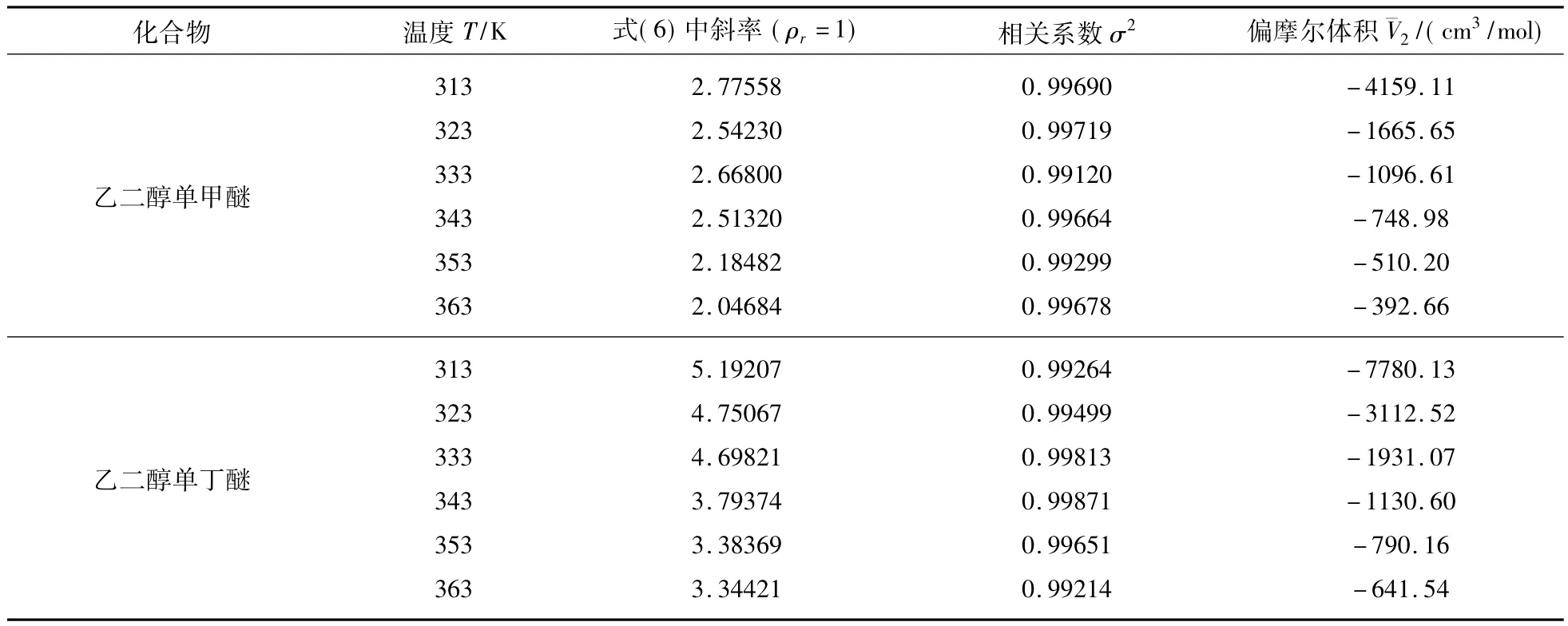
表3 2种化合物于不同温度下超临界体系中的ln x对lnρr(式(6))拟合所得参数Tab.3 Prameters computed by linear fit using ln x vs lnρr in Equation(6)for compounds systems at various temperatures

由表3可见，2种化合物的偏摩尔体积均随温度的升高而减小;溶质在临界点附近的偏摩尔体积难以通过实验而测得，但可由Kumar and Johnston理论进行估算;已有报道［16-18］表明，由 Kumar and Johnston理论所得偏摩尔体积的理论值能与实验测量值较好地吻合;本文根据该理论计算出了乙二醇单甲醚和乙二醇单丁醚在不同温度下的偏摩尔体积(见表3)，为此后2种目标化合物偏摩尔体积的实验测量进行了参考对比的理论工作.

3 结语

当温度313 ～363 K 、压力 8.2 ～18.3 MPa，乙二醇单醚类在超临界CO2中具有较好的溶解性，其溶解度在同温下随压力的升高而增大，在同压下随温度的升高而降低;相比下，同温同压条件下乙二醇单甲醚在超临界CO2中的溶解性优于乙二醇单丁醚，其中当363 K、15.1 MPa时，乙二醇单甲醚在超临界CO2中溶解的摩尔分数高达5.2%.通过2种半经验公式Bartle和Chrastil对2种目标化合物的溶解度进行计算与关联，溶解度的实验值和理论结果能较好吻合，该静态法下测得的溶解度具有较高的准确性;根据Kumar and Johnston理论，由溶解度计算出了乙二醇单甲醚、乙二醇单丁醚在不同温度下的偏摩尔体积，该摩尔体积随温度的升高而减小;由于2种目标物质在超临界CO2中的良好溶解性能，二者可成为新型高效的萃取剂，为研究超临界CO2中有机物质或重金属离子的萃取提供溶解性参考.

［1］Srinivasan M P，Gu Y，Begum R.Imidisation of Langmuir-Blodgett films using a supercritical medium［J］.AColloids and Surfaces A:Physicochem Eng Aspects，2002，198/200:527-534.

［2］Said-Galiyev E E，Vygodskii S Y，Nikitin L N，et al.Synthesis of polyimides in supercritical carbon dioxide［J］.Supercritical Fluids，2003，26:147-156.

［3］Yang H J，Kim H，Guo C Y.Metal ion extraction withbipyridine derivatives as chelating ligands in supercriticalcarbon dioxide［J］.Cleaner Production，2010，38:159-166.

［4］Wang W，Yang H J，Hu J，et al.Extraction of metalions with non-fuorous bipyridine derivatives as chelatingligands in supercritical carbon dioxide［J］.Supercritical Fluids，2009，51:181-187.

［5］Moon S S，Hwayong K.Solubility of iodopropynyl butylcarbamate in supercritical carbon dioxide［J］.Fluid Phase Equilibria，2008，270:45-49.

［6］Sarbu T，Styranec T，Beckman E J.Non-fluorous polymerswith very high solubility in supercritical CO2down to low pressures［J］.Nature，2000，405:165-168.

［7］Du Y，Cai F，Kong D L，et al.Organic solvent-free process for the synthesis of propylene carbonate from supercritical carbon dioxide and propylene oxide catalyzed by insoluble ion exchange resins［J］.Green Chemistry，2005，7:518-523.

［8］Wang W，Yang H J，Hu J，et al.Solubilities of diglycolic acid esters at temperatures ranging from(343 to 363)K in supercritical carbon dioxide［J］.Chemical and Engineering Data，2010，55:694-697.

［9］Xie Y，Yang H J，Wang W，et al.Solubilities of diglycolic acid esters in supercritical carbon dioxide［J］.Chemical and Engineering Data，2009，54:102-107.

［10］Liu J F，Yang H J，Wang W，et al.Solubilities of amide compounds in supercritical carbon dioxide［J］.Chemical and Engineering Data， 2008， 53:2189-2192.

［11］Kawakami T，Saito N，Aiba K，et al.Measurement of static dielectric constants of supercritical fluid solvents［J］.Chemistry Letters，2000，12(6):402-403.

［12］Angus S，Armstrong B，de Reuck K M.International thermodynamic table of the fluid state，carbon dioxide［M］.Oxford:Pergamon Press，1976:269-275.

［13］Bartle K D，Clifford A A，Jafar SA，et al.Solubilities of solids and liquids of low volatility in supercritical carbon dioxide［J］.Physical and Chemical Reference Data，1991，20:713-756.

［14］Darrell L S，L.Antonio E，Rafael Hernandez，et al.Solubility of small-chain carboxylic acids in supercritical carbon dioxide［J］.Chemical and Engineering Data，2010，55:4922-4927.

［15］Kumar S K，Johnston K P.Modeling the slubility of slids in spercritical fuids with dnsity as the idependent vriable［J］.Upercritical Fluids，1988(1):15-22.

［16］Chrastll J.Solubility of solids and liquids in supercritical gases［J］. Chemical Physics， 1982， 86:3016-3021.

［17］Yang H J，Tian J，Kim H.New highly CO2-philic diglycolic acid esters: synthesis and solubility in Supercritical carbon dioxide［J］. Chemical and Engineering Data，2010，55:4130-4139.

［18］Yang Z，Yang H J，Tian J，et al.High solubility and partial molar volume of 2，20-oxybis(N，N-bis(2-methoxyethyl)acetamide)in supercritical carbon dioxide［J］.Chemical and Engineering Data，2011，56(4):1191-1196.