混杂边界轴向运动Timoshenko梁固有频率数值解

胡超荣，丁 虎，陈立群，

(1.上海大学 上海市应用数学和力学研究所，上海 200444，2.上海大学 力学系，上海 200072)

混杂边界轴向运动Timoshenko梁固有频率数值解

胡超荣1，丁 虎2，陈立群1，2

(1.上海大学 上海市应用数学和力学研究所，上海 200444，2.上海大学 力学系，上海 200072)

运用微分求积方法求解两端带有扭转弹簧且弹簧系数均可任意变化的非对称下的轴向运动Timoshenko梁的固有频率。以权系数修改法处理轴向运动Timoshenko梁的混杂边界。研究系统的前两阶固有频率随轴向速度、刚度系数以及弹簧弹性系数变化的情况，并将数值计算结果与半解析半数值的研究结果进行比较，结果表明，数值计算结果与半解析半数值结果基本吻合。

轴向运动梁;Timoshenko模型;固有频率;微分求积法

军事、航空航天以及机械电子工程等研究、制造及生产领域的多种工程元件都可简化为轴向运动连续体模型，比如空中缆车索道、传输带、升降机缆绳等。由于振动因素可能导致这些运输传送装置的效率降低或者造成噪声危害等。因此，轴向运动连续体广受研究者关注［1－10］。

Euler梁模型是轴向运动体系的一种有效的简化经典模型。Öz［1］、冯志华［2］、陈树辉［2］、张伟［4］，Ding等［7］分别利用Euler模型研究了轴向运动梁固有频率、内共振以及静平衡等问题。随着研究的深入，近几年，考虑了更多因素的Timoshenko模型逐渐受到众多研究者的关注。Chen等［8］给出了简支边界的Timoshenko梁模型固有频率的复模态分析方法及半解析半数值求法。Ghayesh和Balar［9］通过半解析半数值方法研究了固定边界的轴向运动Timoshenko梁模型的横向振动固有频率。李等［10］通过半解析半数值方法求解了两端非对称混杂边界的轴向运动Timoshenko梁的固有频率。以上分析可见，Timoshenko梁模型的固有频率求法主要局限于复模态分析结合半解析半数值的求法。该方法的优点在于，在计算固有频率的同时还可以计算模态函数，但是计算过程中的特征函数过于复杂。目前，还没有得到其他方法的验证。

Chen等［7］运用微分求积方法研究了轴向运动Euler梁模型的非线性参数振动，证明微分求积法可用于分析常见边界的轴向运动连续体的横向振动。两端非对称混杂边界是更一般化的边界，一定条件下可以退化为各种常见边界条件，其中包括两端简支、两端固定，以及一端简支一端固定等［10］。本文将引入微分求积方法研究轴向运动Timoshenko梁的横向振动，该方法能够根据常规的矩阵运算，快捷精确的计算系统前几阶固有频率。通过该方法处理更一般的混杂边界，仿真固有频率随系统参数的变化，并与半解析半数值结果［10］比较，验证系统参数对Timoshenko梁模型固有频率的影响。

1 微分求积法及应用

研究在平面内作横向振动的Timoshenko模型轴向运动梁，考虑截面积为A、绕横截面中性轴的转动惯量为J、密度为ρ、初始张力为P的梁以一致的速度沿轴向运动，其速度为常数γ，梁弹性模量为E，剪切模量为G。只考虑梁的横向和径向变形，在径向空间坐标x处，t时刻横向位移为v(x，t)，假设其长度为l，建立轴向运动Timoshenko梁的横向自由振动的无量纲式控制方程［8，10］，利用微分求积法解此运动方程：

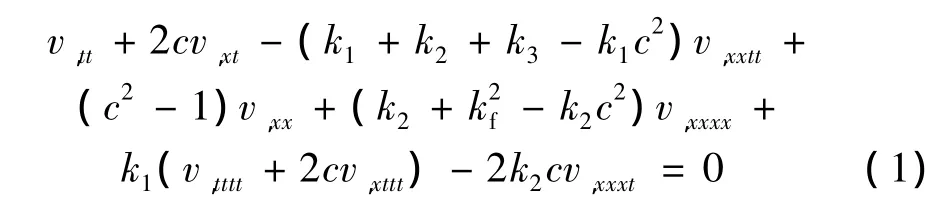
式中逗号后的x和t分别表示对x和t的偏微分，相应的无量纲化变量和参数为［8］：

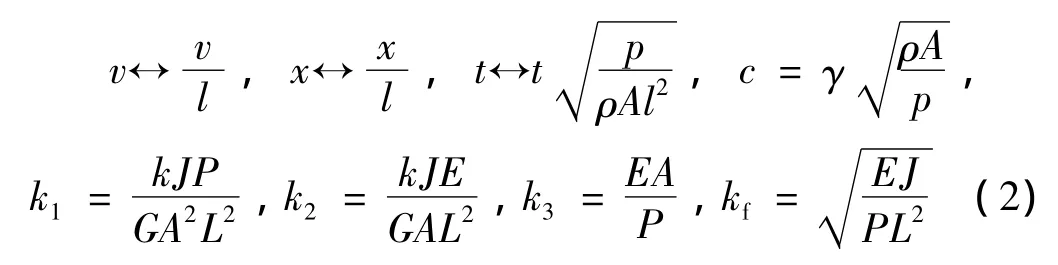
其中，c为速度，k为形状系数，k1和k2为剪切模量，k3为转角，kf为弯曲刚度。取梁两端带有扭转弹簧铰支的无量纲化约束边界条件［10］

其中kt1和kt2为两端边界处的扭转弹簧的刚度。

对函数v(x，t)的空间坐标x进行离散，网格点的分布形式采用非均匀格式［11］：

式中A(r)ij是权系数，r为导数阶数，f(xj)是函数f(x)在网点xj处的值，N表示网点总数，有：

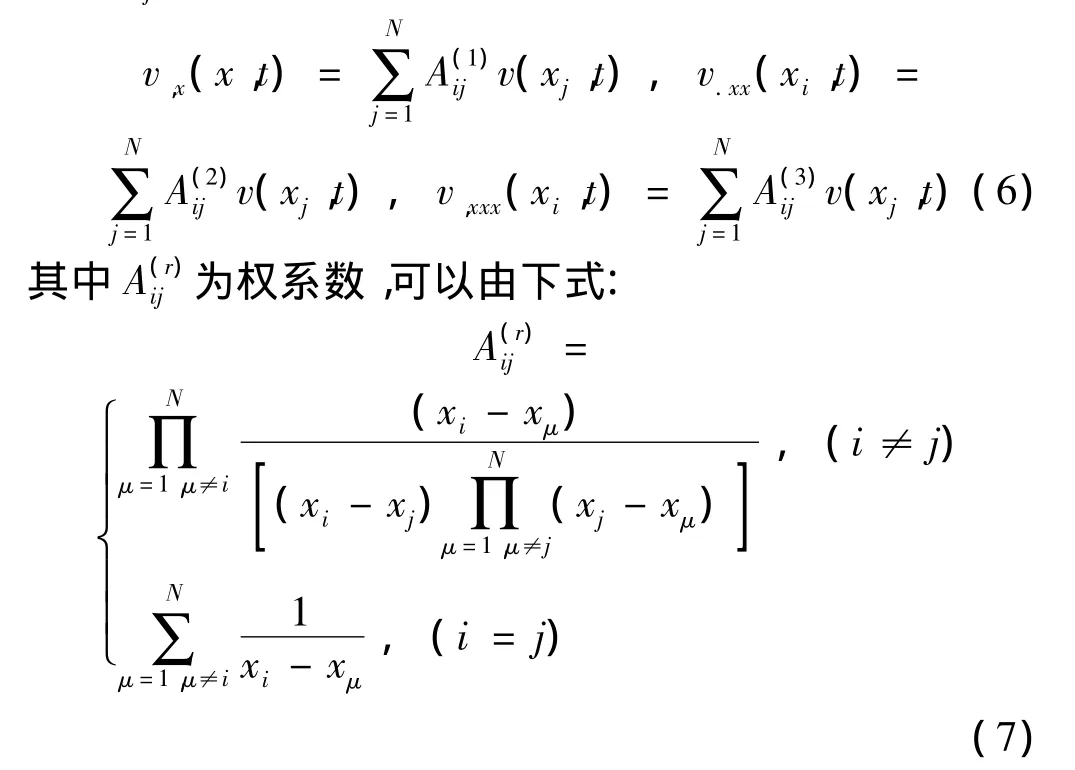
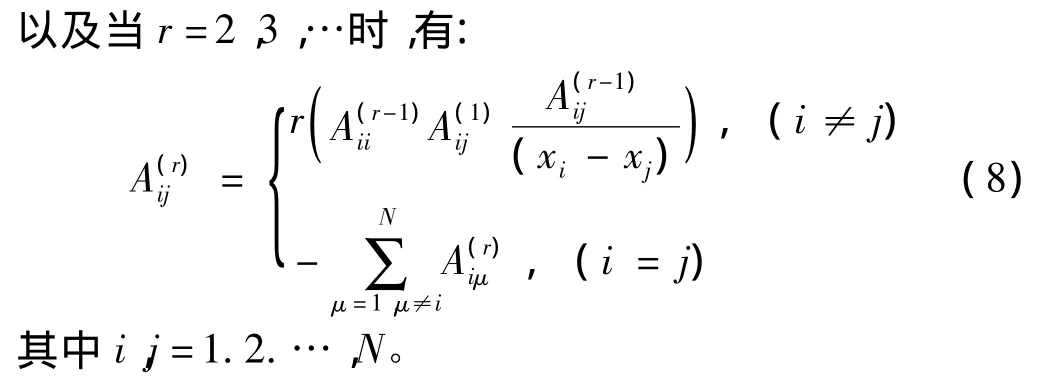
由上述计算公式，将(6)代入控制方程(1)和边界条件(3)，则得到(1)和(3)在相应的网格点的微分求积近似离散方程：

上式中v上面的点表示对时间的导数。

文献［7］研究了微分求积法在轴向运动连续体的应用中的精度问题，并通过数值算例说明，取11个网格节点足够精确。本文在数值计算中也选取11个网格节点，即N=11。

本文采用修正权系数方法来处理非对称混杂边界条件(10)。根据式(10)，在生成(14)式中各系数矩阵时，就将边界条件引入到各权系数矩阵中［11］。修正后的第二阶权系数矩阵为：

其中：

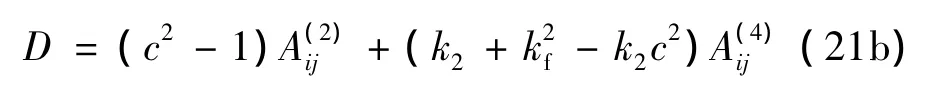
其中 i，j=3，4，…，N －3，N －2。这些都是 N 阶矩阵，而{φ)是N阶列向量。

2 数值结果

Timoshenko梁物理参数［8］分别为 P=107N，A=9 ×10－3m2，E=169 ×109Pa，k=5/6，l=0.3 m，G=66×109Pa;相应无量化参数为 k1=5.90 ×10－5，k2=0.009，k3=0.004 2;图1给出了当c=2，刚度系数为=0.64时，利用微分求积法计算得到的当扭转弹簧取不同弹性系数时，系统的前三阶固有频率随轴向速度变化的数值结果，其中系统参数如图中所示。观察图1，能够清楚看出，轴向运动Timoshenko梁的前两阶固有频率随两端边界处弹簧弹性系数的增大而增大。与以往Timoshenko梁横向振动特性的研究结果相符。

图2给出了当梁刚度系数取不同值的时候，系统的前两阶固有频率随速度变化的情况。由图2可以看出，在轴向运动速度不大于临界速度时，系统的前两阶固有频率随梁的刚度增加而增大，随轴向速度的增大而减小。

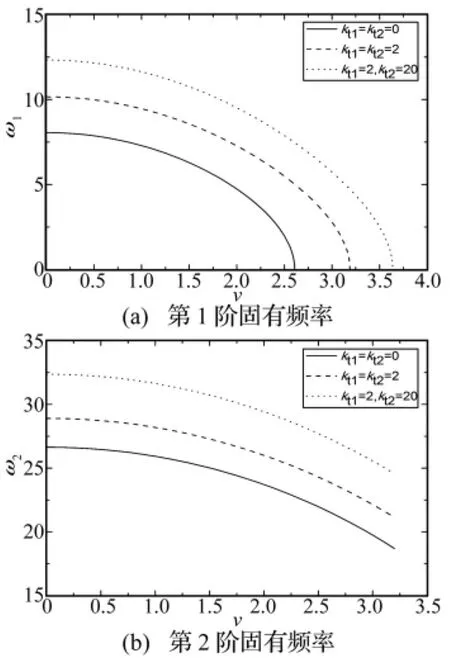
图1 随轴向速度变化的固有频率Fig.1 Natural frequencies changing with axial speed and constraint stiffness

图3给出了当c=2，刚度系数为k2f=0.64时，保持kt2不变，即kt2=2时，系统的前两阶固有频率随弹性系数kt1变化的情况，其中实线表示第一阶固有频率，虚线表示第二阶固有频率。由图3可看出，系统的前两阶固有频率随边界处扭转弹簧的弹性系数增大而增加，尤其是在弹簧系数较小的时候表现的较为明显。如果保持kt1不变，以研究kt2的影响，可得出相同的结论。

3 与半解析半数值结果比较

文献［10］通过假设(1)式的解为复模态形式，通过边界条件建立线性方程组，和模态函数有非零解的充要条件，建立系统的特征方程，这个过程称为解析过程;以数值方法求解特征方程，称为数值过程。这一求解陀螺系统运动频率的方法就称之为半解析半数值的方法。

图4给出了本文结果与文献［10］中的半解析半数值结果的比较，其中弹簧系数取不同的值，梁的刚度系数k2

f=0.64，图中实线为数值计算结果，点线为半解析半数值结果。由图可知在简支边界即kt1=0，kt2=0以及弹簧系数相等即kt1=2，kt2=2时，数值结果与半解析半数值结果吻合的很好;当两端弹簧系数分别取kt1=2，kt2=4时，数值结果与半解析半数值结果在速度较小时吻合很好，但随着速度的增大，两种方法得到的系统第二阶固有频率会有微小的差异。

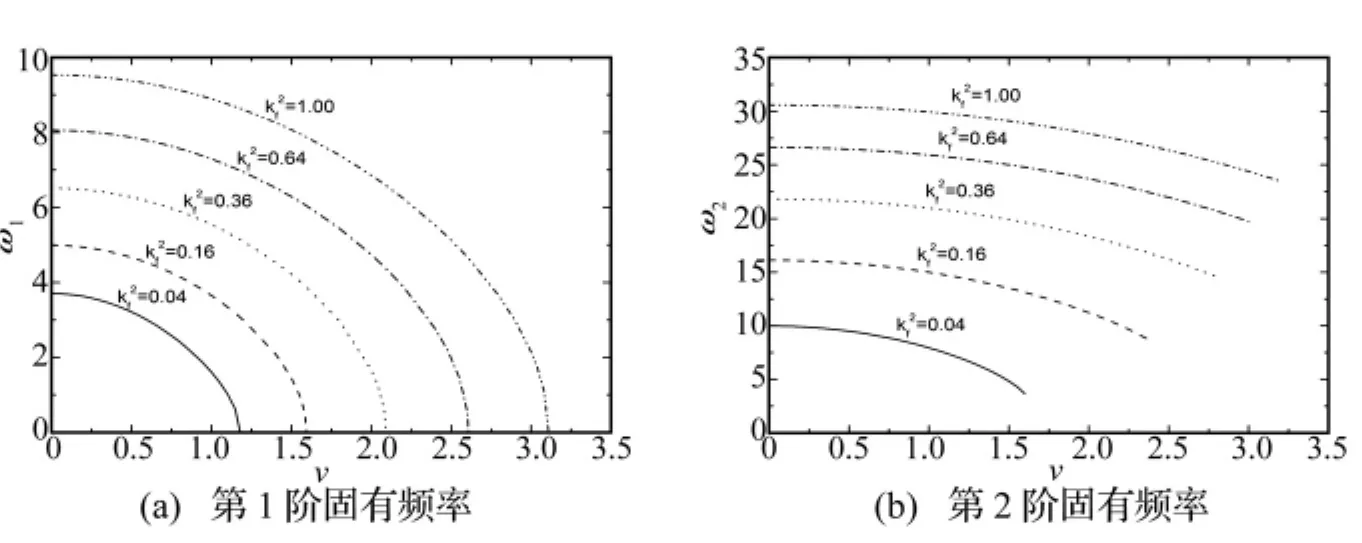
图2 随刚度系数和轴向速度变化的固有频率Fig.2 Natural frequencies changing with axial speed and the stiffness of the beam

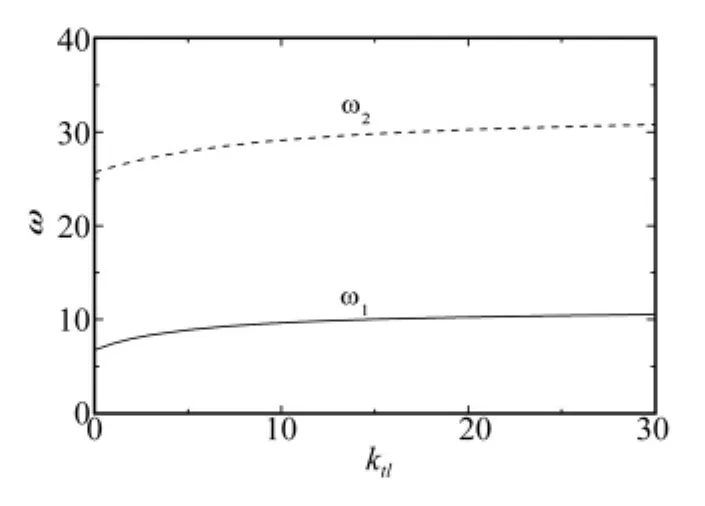
图3 第1和2阶固有频率随着kt1的变化情况Fig.3 The natural frequencies changing with constraint stiffness

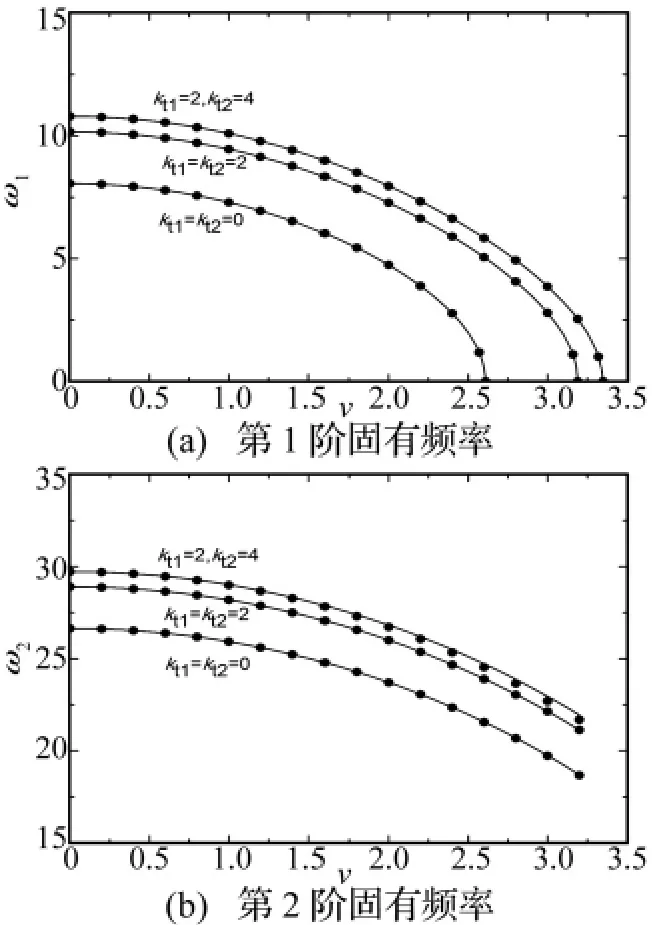
图4 数值结果与半解析半数值结果的比较情况Fig.4 The comparison for the numerical results and the semi－analytical and semi－numerical

4 结论

本文将微分求积方法引入更一般的边界条件，即两端铰支弹簧系数均可任意变化的非对称混杂边界的处理，并求解了这种边界下轴向运动Timoshenko梁的固有频率。数值结果表明，两端弹簧系数的增大以及轴向速度的减小，都会引起系统固有频率的增大，在弹簧系数不大时尤为明显。通过对数值计算结果和半解析半数值的比较，发现本文的数值结果很好的验证了半解析半数值的结论。也说明了微分求积法可以处理这种复杂边界条件。

［1］ Öz H R.On the vibrations of an axially traveling beam on fixed supports with variable velocity［J］.Journal of Sound and Vibration，2001，239：556－564.

［2］冯志华，胡海岩.基础直线运动柔性梁的非线性动力学［J］.振动工程学报，2004，17：126－131.

［3］李映辉，高 庆，蹇开林，等.黏弹性带动力响应分析［J］.应用数学和力学，2003，24：1191－1196.

［4］张 伟，温洪波，姚明辉.黏弹性传动带1∶3内共振时的周期和混沌运动［J］.力学学报，2004，36：443－454.

［5］刘 伟，张劲夫.粘弹性传送带的分岔特性和混沌振动分析［J］.动力学与控制学报，2005，3(3)：63－67.

［6］陈树辉，黄建亮.轴向运动体系横向非线性振动的联合共振［J］.振动工程学报，2005，18：19－23.

［7］Ding H，Chen L Q.Equilibria of axially moving beams in the supercritical regime.Archive Applied Mechanics，2011，81：51－64.

［8］Chen L Q，Tang Y Q，Lim C W.Dynamic stability in parametric resonance ofaxially accelerating viscoelastic timoshenko beams ［J］.Journal of Sound and Vibration，2010，329(5)：547－565.

［9］ Ghayesh M H，Balar S.Non－linear parametric vibration and stability analysis for two dynamic models of axially moving timoshenko beams［J］.Applied Mathematical Modelling，2010，34(10)：2850 －2859.

［10］李 彪，丁 虎，陈立群.非对称混杂边界轴向运动Timoshenko梁横向振动分析［J］.固体力学学报，2009，30(6)：565－570.

［11］ Malink M，Bert C W.Implementing multiple boundary conditions in the DQ solution of higher－order PDE ’s：application to free vibration of plates［J］，International Journal for Numerical Methods in Engineering，1996，39：1237－1258.

Natural frequency numerial solution to an axially moving timoshenko beam with hybrid boundary

HU Chao－rong1，DING Hu2，CHEN Li－qun1，2

(1.Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai 200444，China;2.Department of Mechanics，Shanghai University，Shanghai 200072，China)

The differential quadrature method was developed to solve natural frequencies of an axially moving asymmetric hybrid supported Timoshenko beams with randomly varying spring coefficients at both sides.The weighted coefficient matrices were modified for dealing with the hybrid boundary.The axially moving speed，the stiffness of the beam and the spring coefficients were numerically investigated for clarifying their influences on the first two natural frequencies，and the results were compared with the semi－analytical and semi－numerical solutions.It was shown that both of them are basically consistent.

axially moving beam;transverse vibration;natural frequency;differential quadrature method

O32

A

国家自然科学基金项目(10902064);国家杰出青年科学基金(10725209);上海高校选拔培养优秀青年教师科研专项基金(B37－0101－08－003);上海市优秀学科带头人计划(09XD1401700);上海大学创新基金项目(08－22);上海市重点学科建设项目(S30106);长江学者和创新团队发展计划基金课题(IRT0844)资助

2010－04－12 修改稿收到日期：2010－05－24

胡超荣 女，硕士生，1983年10月生

丁 虎 男，副研究员，1978年3月生