新型人工中耳压电振子设计
刘后广,塔 娜,饶柱石
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
新型人工中耳压电振子设计
刘后广,塔 娜,饶柱石
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
提出利用压电叠堆作砧骨激励式人工中耳的振子,并利用中耳-压电叠堆耦合力学模型对该压电叠堆振子进行辅助设计。该模型基于一无任何听力损伤病史的成年志愿者的左耳,利用CT扫描和逆向成型技术建成。其可靠性通过与实验对比加以验证。最终设计的压电振子只需要10.5 V的有效驱动电压,便可以对镫骨激起相当于鼓膜处90 dB声压激励的振幅。该振子在频率为1 kHz的单伏电压驱动工况下,能耗仅为0.03 mW,满足人工中耳低电压、低能耗的要求。
人工中耳;压电叠堆;有限元分析
听力损伤是国内最常见的疾病之一,据2006年第二次全国残疾人抽样调查显示,国内有2780万听力损伤患者[1]。如今,随着听力学理论的不断充实及耳显微外科手术的迅速发展,相当一部分听力损伤患者得到了有效的治疗,多数传导性听力损伤的患者可以通过手术提高听力。但大部分感音神经性听力损伤目前仍缺乏具有针对性的有效治疗,常规的还是采用佩戴传统助听器的方式来改善听力。而传统助听器只能解决轻度到中度感音神经性听力损伤;佩戴舒适性不佳,患者常常有耳道堵塞的感觉;输出的声音信号和耳道反馈的声音信号混叠,使人感受到的声音信号清晰度降低[2],这些不足使得很多患者不愿意佩戴传统助听器[3]。针对这一问题,国内、外很多机构开始研究中耳植入式助听装置[4-6]。
中耳植入式助听装置又名人工中耳,根据其振子驱动方式的不同可以分为电磁式和压电式两种。其中,压电式较电磁式具有频带宽、能耗小、制造成本低及抗电磁干扰等优点,目前采用该技术的人工中耳主要有:日本Rion公司的Rion Device E-type、美国Envoy Medical公司的Esteem及澳大利亚Cochlear Corporation公司的TICA。临床研究表明,这些压电式人工中耳都能在不同程度上对患者的听力损伤进行补偿。但是,这些人工中耳皆采用了压电双晶片结构,输出增益较小,只能解决传导性听力损伤及中、轻度感音神经性听力损伤。此外,Rion Device E-type与Esteem的植入皆需要切断听骨链,这样势必破坏正常人耳的声音传输功能,且这种破坏是不可逆转的,进而造成进一步的传导性听力损伤。
本文提出了一款新型压电式人工中耳,并对其压电振子进行了初步设计。该人工中耳的植入无需切断听骨链;且其压电振子采用了压电叠堆的形式,输出增益高于传统压电式人工中耳。为了辅助设计该压电振子,文中还建立了中耳-压电振子耦合模型,该模型的可靠性通过与实验对比加以验证。结果表明,该压电振子所需能耗较小,符合人工中耳低能耗要求。
1 新型人工中耳的组成结构
该人工中耳构成及植入位置如图1所示,主要由麦克风、信号处理装置、电源模块及压电振子所构成。其基本工作原理为,系统由麦克风将声音信号采集,再由信号处理单元根据患者听力损失情况进行相应的信号处理,将处理后的信号变成电压信号传给压电振子,通过压电振子的伸缩运动直接驱动听骨链高效振动,继而振动内耳淋巴液,刺激听觉末梢感受器产生听觉。这种直接驱动听骨链的设计更接近生理情况下的听觉产生途径,从而提高了声音保真度。为了提高输出增益,该压电振子采用压电叠堆来实现。

图1 新型人工中耳示意图Fig.1 Schematic of the new type of middle ear implant
2 压电振子结构参数设计
该压电振子主要由压电叠堆构成,故文中主要对该压电叠堆进行设计。
2.1 压电叠堆质量及几何尺寸的确定
该压电振子植入在乳突室内,而人体乳突室空间较小,故所设计的压电振子不能过大。但过小的压电振子又对制造工艺提出了较高要求。综合考虑以上因素,确定其压电叠堆的横截面积为2×2 mm2,高度为2 mm。压电材料选为PZT-4。
2.2 压电振子中压电叠堆层数的确定
由于中耳系统具有复杂的几何形态、超微结构特征,很难通过人体实验来辅助设计中耳植入装置,所以需要借助于中耳力学模型。近几十年,国外在中耳力学模拟上提出了集总参数模型[7]、模拟线路模型[8]及多体动力学模型[9],虽然都对中耳运动机理的研究做出了贡献,但中耳系统较为复杂、且具有非同质性和各向异性的结构组织,这些特性都很难利用前面的解析法进行模拟。有限元法却有这方面的优势,随着计算机运行速度的提高和大型有限元软件的出现,国内、外很多学者都开始这一方面的研究,并将其用在中耳植入器件的研发上[10-12]。文中,为了确定所需的压电叠堆的层数,我们也建立了人体中耳力学模型。
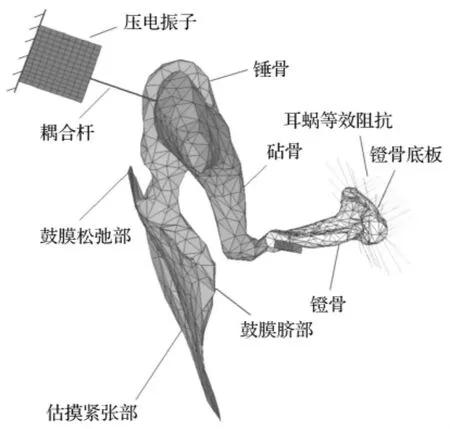
图2 压电叠堆振子-人体中耳耦合力学模型Fig.2 Coupling mechanics model of the piezoelectric stack actuator and the human middle ear
2.2.1 中耳有限元模型
该有限元模型中中耳部分是通过CT扫描一无任何听力损伤病史的成年志愿者左耳,利用逆向成型技术所建成。其中各组织结构的材料属性如表1所列,主要参考文献[13,14]。边界条件如表 2 所列[15,16]。此外,材料泊松比均取为0.3,瑞利阻尼系数取为α=0 s-1,β =0.000 1 s。

表2 中耳有限元模型边界条件Tab.2 Boundary conditions of middle ear FE model
为了验证该模型的可靠性,进行两组对比实验。在模型鼓膜处施加90 dB声压下,计算镫骨底板、鼓膜脐部的位移频响情况,并先后与GAN等人对10例人体颞骨标本所测得的相应数据[17]进行对比,结果分别如图3、图4所示。由图可见,在两组模型对比验证中,模型计算值在低频段均略高于实验测量均值;在中、高频段(>900 Hz)均低于实验测量均值。但总体上,模型计算值在趋势上与实验测量值一致、幅值上也比较接近实验测量值,满足用以预测中耳生物力学特性的要求。
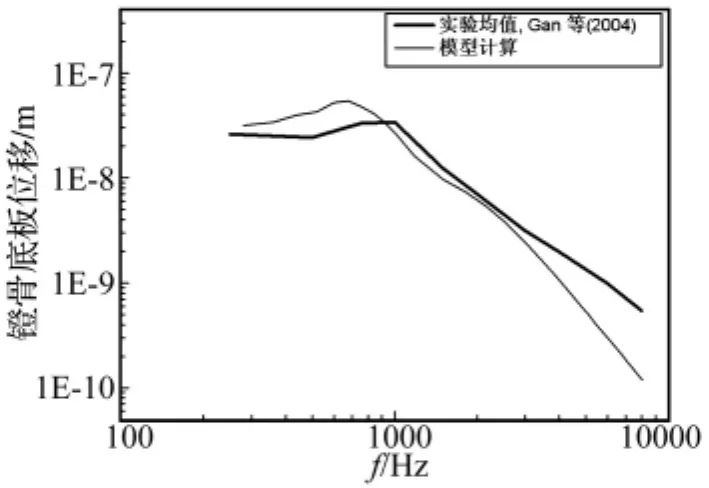
图3 镫骨底板位移对比Fig.3 Comparison of the stapes footplate displacement
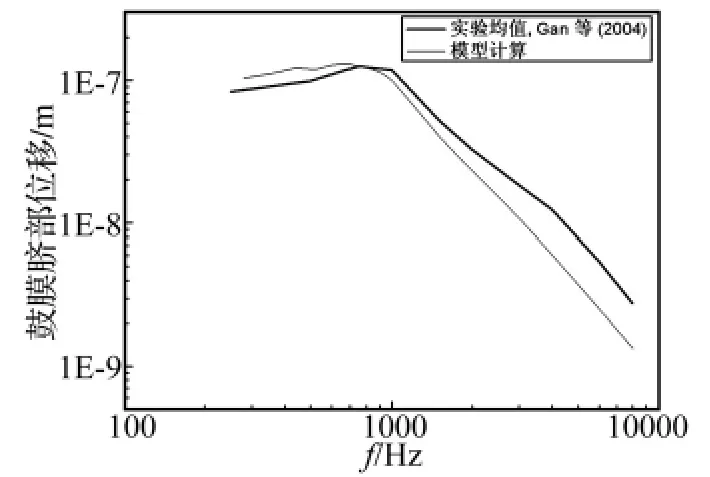
图4 鼓膜脐部位移对比Fig.4 Comparison of the umbo displacement
2.2.2 压电振子与中耳的耦合力学模型
在建立耦合力学模型之前,先建立压电振子中压电叠堆的有限元模型,压电材料选为PZT-4,其材料属性列于表3。压电有限元方程可以写成节点位移U和节点电势 Φ 表达的形式[18,19],如式1所示:
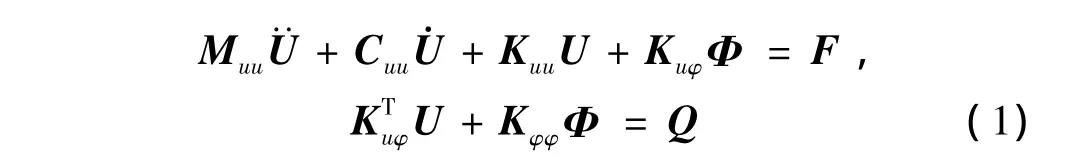
其中,F为力的作用,Q为电场作用。该方程组又可以转化成如下矩阵形式,
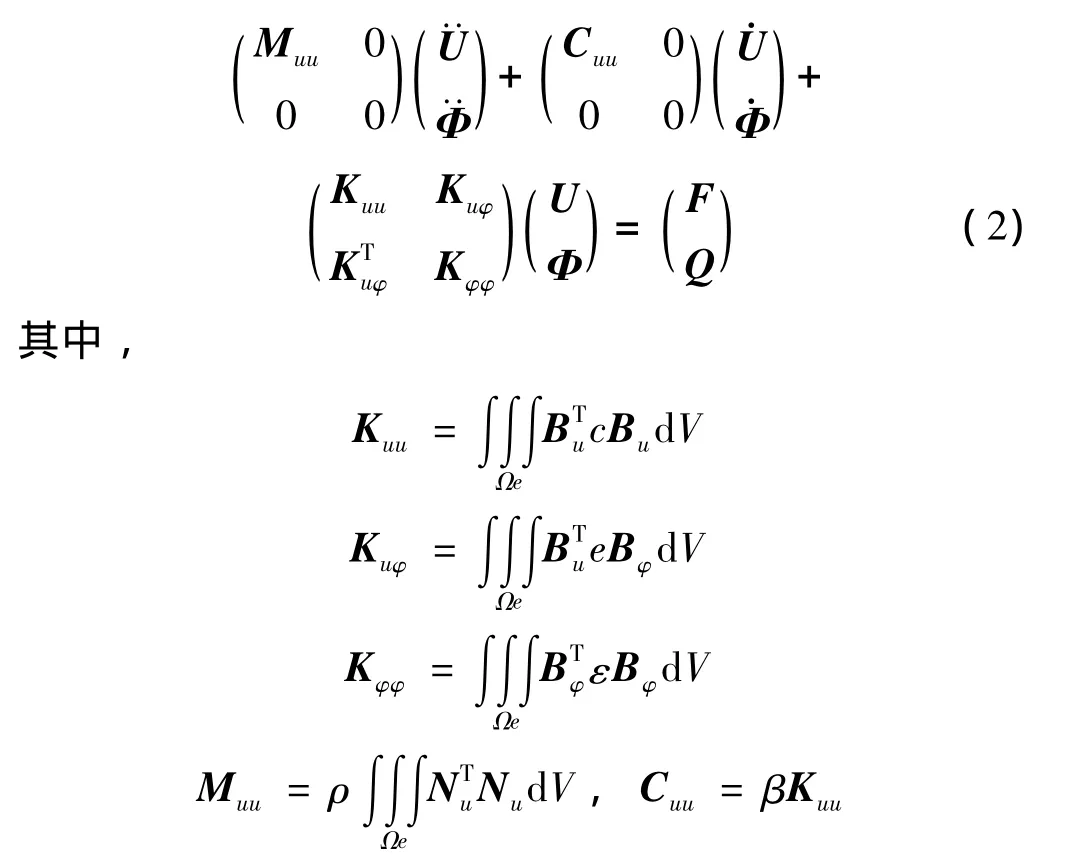
Kuu——机械刚度矩阵
Kuφ——压电耦合矩阵
Kφφ——介电刚度矩阵
Muu——质量矩阵
Cuu——机械阻尼矩阵
Bu,Bφ——形函数倒数
c——弹性系数
e——压电系数
ε——介电常数矩阵
β——阻尼系数

表3 PZT-4材料特性参数Tab.3 Material parameters of PZT-4
再将建立好的压电叠堆有限元模型通过耦合杆与中耳有限元模型合成在一起。耦合杆采用杆单元近似模拟,其一端与压电叠堆顶端上的一节点耦合,另一端与砧骨体上一节点耦合。材料选为生物相容性较好的钛合金,密度为4 500 kg/m3,弹性模量为1.078×105MPa。耦合杆长度为2 mm,横截面积为0.3 mm2。最终建成人体中耳—压电振子耦合有限元模型,如图2所示。
2.2.3 压电叠堆层数的确定
出于安全考虑,压电振子的最大有效驱动电压取为10.5 V[20]。通过以上建立起的耦合模型的数值计算,得到在该电压驱动下压电叠堆层数对振子激振效果的影响如图5所示。从中可见,15层的压电叠堆构成的压电振子便可在10.5 V的有效驱动电压作用下,于低频区对镫骨激励起相应于90 dB声压的激振幅值。且在高频(大于1 kHz)区,这种激励效果更明显,到4 kHz处镫骨被激振幅度相当于120 dB的声压激励(如图6所示)。该激振幅度满足人工中耳的镫骨激振要求[21]。
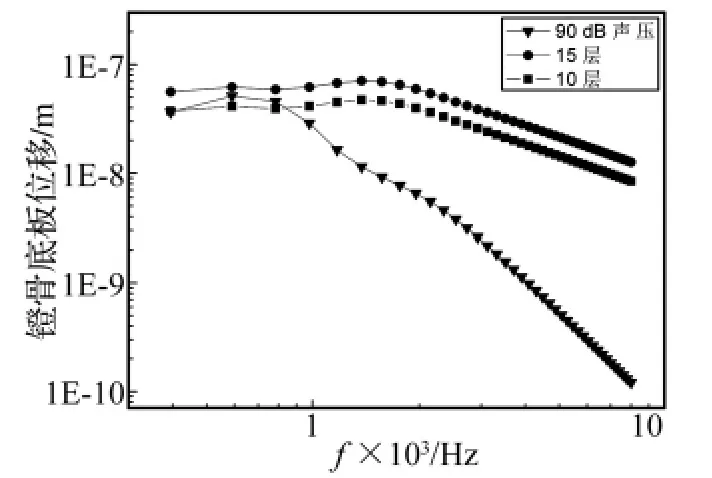
图5 镫骨脚底板位移频响曲线Fig.5 Frequency response of stapes footplate displacement
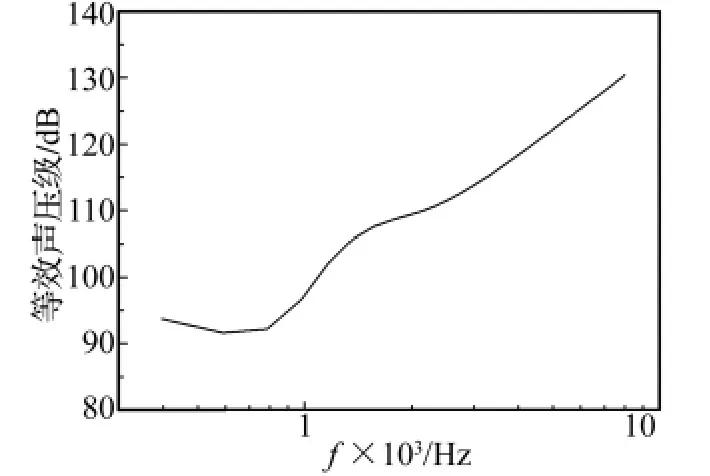
图6 等效鼓膜处激励声压(15层压电叠堆振子在10.5 V rms驱动电压作用下)Fig.6 Equivalent sound pressure levels at the tympanic membrane for the 15 layer’s piezo-stack actuator excitation at 10.5 V rms
3 振子能耗分析
人工中耳属于植入装置,其振子能耗不能过大,文[21]报道的压电振子能耗量仅为2.5 mW。故需对文中的压电叠堆式振子的能耗进行分析。
压电片工作频率远低于其固有频率时,其能耗特性可以近似为一电容器[22]。压电叠堆的近似电容可由其所有单层压电片的近似电容累加得到,如式(3)所示:

其中ε0为真空中介电常数;ε33为相对介电常数;A为叠堆电极表面积;t为单层压电片的厚度。压电叠堆在驱动频率为f的正弦电压Vrms驱动下,有效电流Irms及相应的能耗Prms分别为:

根据以上公式计算可得,该PZT-4叠堆构成的压电振子的近似电容为6.4 nF;有效电流为0.04 mA;在1 kHz的单伏电压驱动下能耗量为0.03 mW。该压电振子在10.5 V有效电压驱动下,能耗也仅为3.09 mW,满足人工中耳的低能耗要求。
4 结论
本文设计了一款新型人工中耳的压电振子,该振子由压电叠堆来实现。考虑到植入空间及制作工艺的限制,该压电叠堆的横截面积取为2×2 mm2,高度为2 mm。压电叠堆的材料选为PZT-4。该压电振子的植入不会对患者听骨链造成过大损伤。通过压电叠堆—中耳耦合力学模型的数值计算,最终确定压电振子中压电叠堆的层数为15。该压电振子在10.5 V最大有效驱动电压作用下,能耗仅为3.09 mW,满足人工中耳的低能耗要求。此外,该压电振子的高频段增益较大,考虑到大部分感音神经性听力损伤多发生在高频段,故该特性对患者的听力补偿特别有利。
[1]第二次全国残疾人抽样调查办公室.第二次全国残疾人抽样调查资料[M].北京:中国统计出版社,2007.
[2]Meister H,Lausberg I,Kiessling J,et al.Determining the importance of fundamental hearing aid attributes[J].Otol Neurotol,2002,23(4):457 -462.
[3]Davis A.Population study of the ability to benefit from amplification and the provision of a hearing aid in 55-74-year-old first-time hearing aid users[J].Int J Audiol,2003,42(Suppl 2):2S39-2S52.
[4]Haynes D S,Young J A,Wanna G B,et al.Middle ear implantable hearing devices:an overview [J]. Trends Amplif,2009,13(3):206 -214.
[5]郭继周,汪若峰,刘 莎,等.植入式人工中耳听器-GW1型的研制及动物实验研究[J].耳鼻咽喉-头颈外科,1994,1(4):237-240.
[6]王应丰,沈高飞,塔 娜,等.声桥系统压电植入振子力学建模及参数优化[J].振动与冲击,2009,28(3):108-111.
[7] Hudde H,Weistenhofer C.A three-dimensional circuit model of the middle ear[J].Acustica United with Acta Acustica,1997,83(2):535-549.
[8]Feng B,Gan R Z.Lumped parametric model of the human ear for sound transmission [J]. Biomechan Model Mechanobiol,2004,3(1):33 -47.
[9] Eiber A,Freitag H G.On simulation models in otology[J].Multibody System Dynamics,2002,8(2):197-217.
[10]姚文娟,李晓青,李 武,等.中耳病变及人工镫骨形体研究[J].医用生物力学,2009,24(2):118-122.
[11] Gan R Z,Dai C,Wang X,et al.A totally implantable hearing system-design and function characterization in 3D computational model and temporal bones [J].Hear Res,2010,263(1-2):138-144.
[12] BornitzM, Hardtke H J, ZahnertT. Evaluation of implantable actuators by means of a middle ear simulation model[J].Hear Res,2010,263(1 -2):145 -151.
[13] Sun Q,Chang K H,Dormer K J,et al.An advanced computer-aided geometric modeling and fabrication method for human middle ear [J].Med Eng Phys,2002,24(9):595-606.
[14] Beer H J,Bornitz M,Hardtke H J,et al.Modeling of components of the human middle ear and simulation of their dynamic behavior[J].Audiol Neurootol,1999,4(3 - 4):156-162.
[15] Prendergast P J,Ferris P,Rice H J,et al.Vibro-Acoustic modelling of the outer and middle ear using the finite-element method[J].Audiol Neurootol,1999,4(3-4):185-191.
[16] Sun Q,Computer-integrated finite element modeling and simulation of human middle ear[D].Oklahoma:The University of Oklahoma,2001.
[17] Gan T Z,Wood T W,Dormer T J.Human middle ear transfer function measured by double laser interferometry system[J].Otol Neurotol,2004,25(4):423 -435.
[18] Lerch R.Simulation of piezoelectric devices by two-and three-dimensional finite element[J].IEEE Transactions on Ultrasonics Ferroelectric and Frequency Control, 1990,37(2):233-247.
[19] Ostergaard D F,Pawlak T P.Three-dimensional finite e lements for analyzing piezoelectric structures[C]//IEEE Ultras-onics Symposium, Williamsburg, USA, November 17-19,1986:639-644.
[20] Laursen W.Breaking the sound barrier[J].Engineering &Technology,2006,1(3):38-41.
[21] LeysiefferH, Baumann JW, MullerG, etal.An implantable piezoelectric hearing aid transducer for sensorineural hearing loss.Part I:Development of a prototype[J].HNO,1997,45:792-800.
[22]Wang Z G,Abel E W,Mills R P,et al.Assessment of multi-layer piezoelectric actuator technology for middle-ear implants[J].Mechatronics,2002,12(1):3 -17.
Design of a new type of piezoelectric actuator for middle ear implant
LIU Hou-guang,TA Na,RAO Zhu-shi
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai 200240,China)
A piezoelectric stack actuator for incus driving type middle ear implant was proposed and designed.To aid the design,a coupled mechanical model between a human middle ear and a piezoelectric stack actuator was constructed.This model was built based on a complete set of computerized tomography section images of a healthy volunteer's left ear with reverse engineering technology.The result showed that the stapes footplate displacement stimulated with the designed piezoelectric stack actuator's excitation at 10.5 V rms is equivalent to that from acoustic stimulation at 90 dB SPL,adequate to the ossicular chain;the corresponding power consumption is 0.03 mW per volt of excitation at 1 kHz,low enough to meet the requirements of a middle ear implant.
middle ear implant;piezoelectric stack;finite element analysis
TH785.1
A
国家自然科学基金(10772121);上海交通大学医工交叉研究基金(YG2007MS14)
2010-04-23 修改稿收到日期:2010-06-24
刘后广 男,博士生,1982年9月生
饶柱石 男,教授,博士生导师,1962年生

