一类混杂系统的预测控制设计

邹媛媛 贾廷纲 牛玉刚(.华东理工大学 信息科学与工程学院，上海 0037;.上海电气集团股份有限公司中央研究院，上海 0003)

0 引言

分段线性(Piecewise Linear，PWL)系统作为一类基本的混杂动态系统模型，能够用来描述许多工程实际系统中的混杂特性，如饱和、继电器、死区等环节［1，2］，也可以用来近似非线性系统。因此，对PWL系统控制问题的研究具有重要的理论和实际意义。

目前，预测控制已经被成功应用于 PWL系统［3-7］，其中，PWL系统预测控制的稳定性综合问题是大家关注的焦点［5，6］。针对这个问题，本文对含有两个子系统的连续时间PWL系统进行预测控制器设计。首先，对每个子系统，设计有界控制器，在此基础上，提出一种预测控制和有界控制相结合的混合控制方法，并给出子系统之间的稳定切换规则，从而保证系统的全局稳定性。这种方法的好处是只需要对每个子系统求解二次规划问题，避免了对整个PWL系统求解含有逻辑变量的二次(或线性)规划问题，降低了算法的复杂度。

1 有界控制

考虑如下的连续时间PWL系统

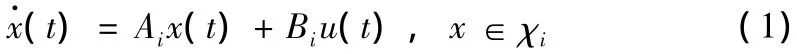
其中，x(t)=［x1(t)…xn(t)］T∈Rn是状态向量，u(t)=［u1(t)…um(t)］T∈U⊆Rm是控制输入向量。U是输入约束，定义为U∶=系数矩阵分别为 Ai∈Rn×n，Bi∈Rn×m，i∈

考虑第i个子系统，设其Lyapunov函数为Vi=xTPix，存在满足Ricatti方程

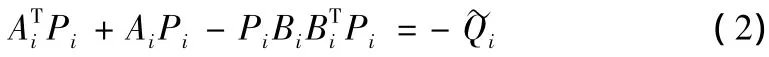
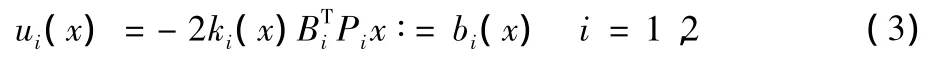
其中

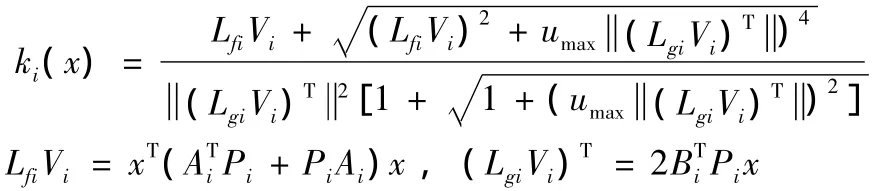
我们发现，如果状态轨迹满足如下条件

那么，根据Lyapunov理论，有界控制器(3)满足输入约束，并且Lyapunov函数是单调递减的。利用集合Φi(umax)，可以构造一个包含在Φi(umax)的最大椭圆集作为稳定域

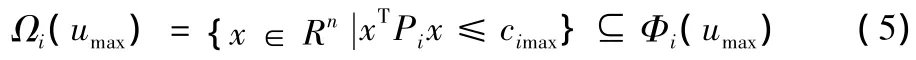
其中，cimax＞0是满足Ωi(umax)⊆Φi(umax)的最大值。

对于系统(1)来说，稳定域估计集可以如下构造。假设S∶≜为状态分区的边界

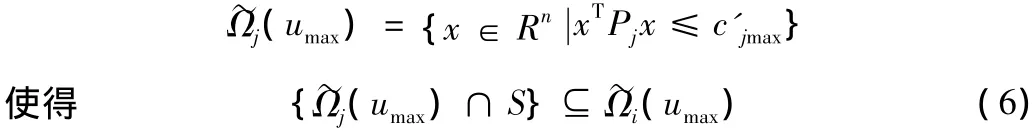
其中，c'jmax是满足条件的最大值。则系统(1)的稳定域估计集

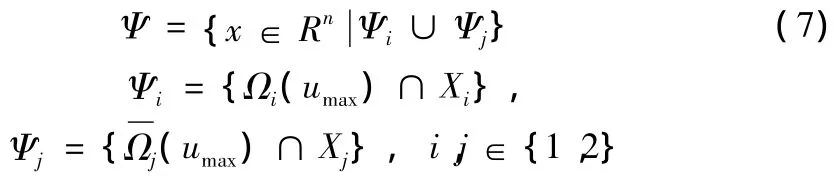
使得

其中，c'imax、c'jmax是满足条件的最大值。则含系统(1)的公共的稳定域估计集为(7)的形式，

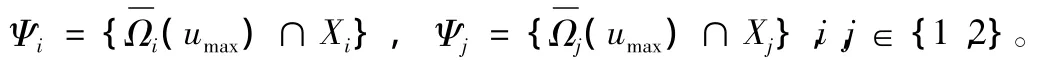
定理1 考虑系统(1)，对第i个子系统，通过构造Lyapunov函数Vi，得到该子系统的有界控制器(3)，稳定域估计集Ψ。假设初始状态为 x0∈Ψi，i∈{1，2}。如果在时刻

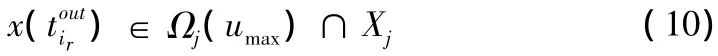
那么状态切换到第j个子系统，反复此控制过程，可得闭环系统是渐近稳定的。其中是第r次离开第i个子系统的时间为第m次进入第j个子系统的时间为第m-1次进入第j个子系统的时间。

虽然定理1给出的有界控制策略能够保证闭环系统稳定，但是，有界控制对系统的最优性没有要求，因此在有界控制的作用下系统的控制性能较差。

2 混合预测控制

由于预测控制是在最优性能指标的情况下，求解满足系统状态和输入约束的控制律，因此，其具有良好控制性能。基于上述分析，本文将预测控制和有界控制相结合，在系统的稳定域估计集内，采用两种控制律切换模式以达到系统稳定性和最优性的兼顾。

2.1 子系统预测控制

针对系统(1)的每个子系统，设计相应的预测控制器。考虑第i个子系统，x(t)为系统在t时刻的状态，可以通过求解如下优化问题得到预测控制

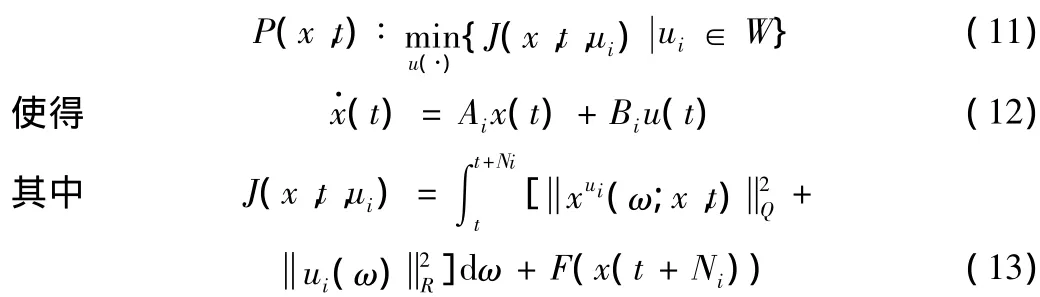
W=W(t，Ni)是一组由［t，Ni］映射到 U 的分段连续函数，Ni是预测时域，{ui［k］=ui(kT)}为要求的控制序列，满足:ui(·)∈W ，ui(t)=ui［k］，t∈［kT，(k+1)T］，T 为采样周期。xui(ω;x，t)是式(12)的解，Q和R是严格正定对阵矩阵，F是终端加权。

在时段［kT，(k+1)T］内，通过求解上述优化问题，可以得到一组预测控制序列。通常我们只采用第一个(·)∈W，即

作用到第i个子系统。

2.2 混合预测控制

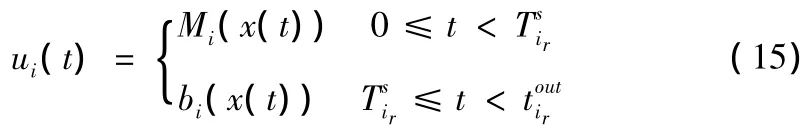
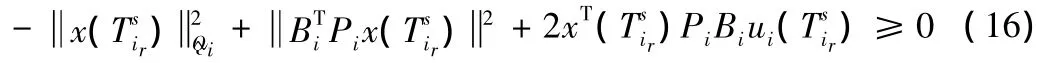
3 仿真研究

为了验证混合预测控制的有效性，考虑下面例子

针对(17)描述的两个子系统，分别考虑对应的Lyapunov函数 xTPix。取，通过求解 Ricatti方程，可知

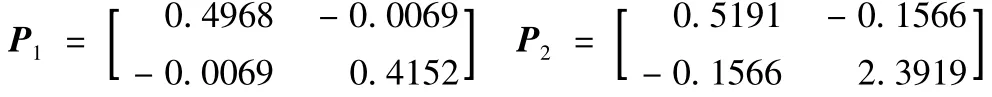
根据(7)的描述形式，系统(17)的稳定域估计集，预测控制目标函数的参数选择为 Q=2×I2，R=0.1，时域长度 T=0.4。取初始状态为x0=［23］T∈Ψ1，采用定理2提出的混合预测控制策略，闭环系统状态轨迹渐近到达原点。

4 结论

本文针对一类混杂系统，提出了一种保证闭环系统稳定性的预测控制策略。对每个线性子系统，分别设计相应的有界控制器，并在此基础上，基于子系统之间的状态切换条件构造出系统的稳定域估计集。在稳定域估计集内，给出有界控制和预测控制相结合的控制策略，保证了不同子系统之间切换的稳定性。

［1］ SONTAG E.Nonlinear regulation:The piecewise linear approach［J］.IEEE Transactions on Automatic Control，1981，26(2):346-358.

［2］ 张聚.混杂系统理论及在非线性系统中的应用研究［D］.浙江大学，2005.

［3］ 邹媛媛，邹涛，李少远.混杂系统的预测控制.控制与决策，2007，22(4):361-365.

［4］ 丁宝苍.预测控制的理论与方法［M］.北京:机械工业出版社，2008.

［5］ 曾锋，高东杰，李秀改.一类有约束的分段线性系统双模预测控制.控制与决策，2006，21(5):597-600.

［6］ ÖZKAN L，KOTHARE M V，GEORGAKIS C.Model predictive control of nonlinear systems using piecewise linear models［J］.Computers and Chemical Engineering，2000，24(2-7):793-799.

［7］ LAZAR M，HEEMALS W P M H.Predictive control of hybrid systems:Input-to-state stability results for sub-optimal solutions［J］.Automatica，2009，45(1):180-185.

［8］ El-Farra N H，Mhaskar P，Christofides PD.Uniting bounded control and MPC for stabilization of constrained linear systems［J］.Automatica，2004，40(1):101-110.