传染病监测数据的统计分析方法

朱 琦 于石成 郝元涛△

传染病监测数据的统计分析方法

朱 琦1于石成2郝元涛1△

1.广州市中山大学公共卫生学院医学统计与流行病学系(510080)

2.国家疾病预防控制中心(102206)

△ 通讯作者：郝元涛，E-mail：haoyt@mail.sysu.edu.cn

有效的传染病控制，依赖于有效的传染病监测〔1〕。传染病监测是对人群传染病的发生、流行及影响因素进行有计划的、系统的长期观察，以达到控制传染源，切断传播途径，保护易感人群的目的。以上每一步的实现都需要建立在对监测数据合理分析的基础上。

在美国，传染病监测数据每周会汇总发布在美国CDC出版的《患病率及死亡率周报》上，主要是以图表的形式对各种传染病的三间分布进行回顾性的描述。在2001年以后，美国CDC不断将一些新的分析方法整合入传染病监测数据的分析体系，将监测数据的利用从回顾性简单描述领域拓展到前瞻性分析领域，尝试从常规报告数据中发现早期异常，并对传染病的流行趋势进行预测〔2〕。

2003年SARS之后，我国在传染病监测系统的建设上投入大量的资源，目前已经建成了覆盖全国的传染病信息报告网络，能够收集全国范围的传染病监测数据。但收集的数据内容较少，主要是发病的信息，缺少环境、社会人口学等详细的信息;同时由于存在漏报和重复报告，数据的质量需进一步提高。这些问题为传染病监测数据的统计分析带来了挑战。

我国传染病监测数据的利用仍停留在简单描述阶段，缺乏传染病相关危险因素的研究，缺乏利用高级的统计分析方法，前瞻性地预测传染病未来的流行趋势。虽然有很多学者利用国外的方法，对传染病的流行进行前瞻性预测，但是这些研究都是分散的，并没有整合到传染病监测数据分析的体系中，同时由于各个国家的疾病监测系统收集的数据内容不同，不能简单地将国外的统计方法照搬到国内。鉴于我国传染病监测系统收集的数据内容有限，如何利用有限的数据，挖掘出最大的信息;如何利用其他方面收集的数据(同期社会人口学资料、环境资料)，将其与监测数据相结合，扩展分析领域，是一个具有重要现实意义的课题。

本文旨在通过文献综述的方式，归纳阐述国内外已经开发的，能够应用于传染病监测数据的统计分析方法，包括回顾性的分析方法和前瞻性的分析方法。

传染病监测数据的统计分析方法

传染病监测系统所收集的数据总量十分庞大，数据分析处理的方式也是多种多样。对于数据的分析可分为回顾性和前瞻性两种;按照时间段的不同又分为周分析、月分析和年度分析。各种类型的分析用途不同，欲解决的公共卫生监测问题也是不同的〔3〕。

对于传染病监测数据的回顾性、描述性的统计分析方法已经较为成熟和模式化，主要是通过一些统计图表的形式将不同时间、不同地区、不同人群的传染病发病情况刻画出来。现阶段这一领域的研究热点是：如何根据现有的监测数据，判断传染病的发病是否具有空间和时间聚集性(如何早期识别传染病的爆发)。

在监测数据的前瞻性研究领域，目前研究较多的，是如何利用现有的传染病监测数据，对未来传染病的流行趋势进行预测。这类分析方法大致可以分为三大类：时间分析方法、空间分析方法、其他分析方法。

1.时空聚集性分析方法

此类方法的思想是在考虑了地区人口差异，对人口空间分布进行校正的前提下，检验疾病的时空分布是否随机。根据检验目的可以分为焦点聚集性检验和一般聚集性检验。

焦点聚集性检验用于检验在一个事先确定的点源附近是否有局部聚集性存在。而一般聚集性检验是在没有任何先验假设的情况下对聚集性进行定位〔3〕。一般聚集性检验又可以分为聚集性探测检验和全局聚集性检验。聚集性探测检验是在没有先验假设的情况下对局部聚集性进行定位，并确定其统计学意义。而全局聚集性检验是用于确定在整个研究区域是否存在聚集性，并不考虑单个聚集性的统计学意义〔4，5〕。

(1)聚集性探测检验

主要的方法有Kulldorff空间扫描统计量、Besag_Newell方法〔3〕、Turnbull 方法〔6〕、最大超额事件检验〔7〕。

其中应用较多的是Kulldorff空间扫描统计量，其思想是在地图上构造一个圆形扫描窗口，并让其在研究区域内移动，扫描半径从零连续递增到预先规定的上限，继而产生无数个半径不同的窗口，计算每个窗口内外的似然值，似然值最大的窗口被认为是最不可能因为随机而造成的 cluster〔8〕。2005年，Toshiro Tango和Kunihiko Takahashi对Kulldorff法进行了改良，将扫描窗口拓展为任意形状，而不是仅仅限定为圆形〔9〕。

(2)全局聚集性检验

主要的方法有 Bonetti-Pagano的 M 统计量〔10〕、Cuzick_Edwards方法〔11〕、Oden 方法和 Ipop 方法〔12，13〕、Mantel方法〔14〕、k 个最邻近法〔15〕。

其中k个最邻近法是最新的方法，由Jacquez于1996年提出，其目的是检验在空间上相邻的病例，在时间上也相邻。Norstorm等应用了此方法研究了挪威牛群急性呼吸道传染病的时空聚集性〔15〕。

2.时间分析方法

这一类统计学方法用于探测公共卫生监测时间序列数据中的异常。其思想是基于传染病的历史水平，制定数学模型并根据模型计算出预期值，然后比较实际值与预期值之间的偏移量，对模型的预测效果做出评价并将模型应用于实际工作中。

(1)历史极限法〔16〕

将传染病当前4周的发病数与基线进行比较，这一基线是过去5年相应的前面4周、当前4周和之后4周病例数的平均值。得到前面5年的15个数值后，用当前4周的合计病例数除以15个数值的平均值，得到一个比值，并将这个比值在对数坐标中表现出来，与比值的历史极限进行比较。比值历史极限的计算公式为：1±，其中均数μ和标准差σ是通过15个历史数据计算得到的。

该方法的优点是简单易用，能够提供病例每周异常状况的总结。但同时存在3个缺陷：并未考虑对趋势的探测;忽略了数据之间的相关性;正态性假设不一定成立，尤其对于罕见疾病。

(2)过程控制图

过程控制图的基本思想是：如果某随机变量独立并且服从正态分布，可以构造出一个统计量y，当y超过预先确定的控制界限时，就认为研究过程脱离统计控制，即出现统计学失常，提示存在非正常事件〔17〕。适当的控制界限的选择显得非常重要〔17〕。常用的控制界限的上下限通常表示为过程的标准差的倍数(如3倍标准差)。常用的过程控制图包括：Shewhart图、累积控制图(累积和法)、移动平均图、指数加权移动平均图。

Shewhar图用于探测过程均数的非随机偏移，对异常观察值发出警报。

累积和法是将观察值与预期值的差值进行累加，若超过了预先确定的阈值则发出警报。

移动平均图是 Stern and Lightfoot〔18〕于 1999 年提出的一种自动预警系统，并应用于肠道病原体监测数据。移动平均图的统计量为：

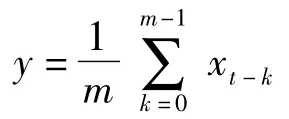
其中m是移动平均中用到的过去观察值的个数。当|yt|超出控制限时即认为出现统计失常。移动平均图探测较小变化的能力比较强，其中m是关键参数，决定了图的适用性，适当的m能使控制图在假阳性率和假阴性率之间取得平衡。

(3)时间序列分析

传染病监测数据通常表现出相关性和季节性，对疾病未来的发病率进行预测时必须充分考虑到数据的这些特点。时间预测的本质就是利用目标本身的动态时间序列、分析、研究预测目标未来的变化规律。

时间序列分析最早应用于计量经济学，后来才慢慢延伸到医学领域。时间序列预测方法主要有：指数平滑预测、移动平均预测、自回归移动平均模型(ARIMA模型)等〔19-22〕。其中ARIMA模型是最为经典的模型。

ARIMA模型建模过程主要按4个阶段进行。序列平稳化：ARIMA的应用需要时间序列符合平稳性的要求。模型的识别：主要是根据ACF图和PACF图的特征，提出几种可能的模型作进一步分析。模型参数估计和模型诊断：对提出的模型进行参数估计和诊断，如模型不恰当，则回到第二阶段，重新选定模型。预测应用：将最终建立的恰当的模型，应用于未来传染病流行趋势的研究〔20〕。

ARIMA模型被用于包括监测数据的分析在内的很多领域，美国CDC所开发的公共卫生监测统计软件(SSSI)提供的很多用于分析监测数据的模型中，就包括ARIMA模型。

在ARIMA模型被提出以后，有很多学者针对该模型进行了进一步的完善，例如将过程控制图与ARIMA模型相结合〔17〕，将小波分析与 ARIMA模型相结合〔23〕。这些完善扩展了ARIMA模型的适用范围，提高了预测的准确度。

3.空间分析方法

为了研究传染病的空间变化情况，预测传染病在各个地区未来的发病趋势，就需要将传染病监测与空间技术(用于寻找和描述地图上的聚集程度)结合起来〔24，25〕。地理信息在传染病监测中的最早应用可以追溯到1854年John Snow对伦敦宽街爆发的霍乱疫情的流行病学调查。近年来随着传染病监测系统的发展和数据收集量的增加，对于传染病空间聚集性探测的需求也与日俱增。

当监测系统收集到病例时，可以即时对病例进行定位，也可从保存有符合监测条件的患者地理定位的静态数据库中调用数据〔24〕。地理编码最简单的形式是区号或邮编，也可以通过地理信息系统(GIS)得到详细的经纬度坐标〔26，27〕。统计学中将这种有地理信息的数据称为空间数据。

尽管疾病的时间监测方法已经有了很好的发展，但用于空间监测的方法研究并不多。空间监测统计方法(从空间上探测传染病的聚集性)已经成为未来研究的热点。

用于迅速探测空间趋势的方法主要有以下几种：

(1)广义线性模型和广义线性混合模型

当可以得到局部区域内每一个病例的地理定位时，Kleinman等〔28〕提出了可以采用广义线性模型进行监测。该方法简称为“SMART分值法”(small area regression and testing scores)。其思想是将每一个小区域当作一个个体，并拟合随机效应来考虑每个区域的重复数据。这一方法允许每个小区域病例的基线发病率存在变异。

SMART分值法可容纳时间聚集性、长期趋势、季节性，并对每一区域居住人群的不同特征进行校正。该模型的结果可以用基于概率的矩阵表示，该结果对协变量和多重比较都进行了校正。目前该模型已经可以由多种软件实现。

(2)Rogerson空间累积和法

Rogerson在累积和法的基础上加入了空间统计量，将其应用扩展到传染病的空间分析领域〔29〕。

Raubertas〔30〕对 Rogerson 空间累积和法进行了完善，提出对多个地区进行监测时，应保留每个地区及其周围临近区域的累积和，而不是只保留每个地区的累积和。具体做法是构建每个地理单位的局部统计量，即区域内及其周围区域的观察值的加权和，离该区域的距离越远，权重越小。最后监控这些局部统计量的累积和。

由于累积和法是对实际值和预期值的差值进行累计，因此，采用Rogerson的方法的关键就是如何较好地计算预期值〔31〕。如果预期值的计算不准确，最终发出警报的可能是模型的误差，而与真正疾病发病率的改变无关。

4.其他分析方法

(1)SIR模型

SIR模型是通过研究传染病的易感者(susceptible)、感染者(infected)以及移出者(removed)随时间变化的情况，对传染病未来的流行趋势和流行规模进行预测，是应用于传染病预测的经典数学模型〔32〕。

(2)模糊数学理论

模糊数学理论不需要知道输入量和输出量之间的函数关系，已经有学者将其中的模糊聚类法和模糊控制模型应用于传染病的预测领域。向立富应用模糊综合评判法对1970年至1980年流脑的发病率进行回顾验证，证明模糊控制模型的回代准确率为81.1%〔33〕。

(3)马尔科夫链

马尔科夫链是应用概率论来研究随机事件变化趋势的一种方法，其主要思想是：将时间序列看作一个随机过程，通过对事物不同的初始状态来预测未来的情况，其中系统在每个时间所处的状态是随机的，从当前时间到下一时间的状态按一定的概率转移，而未来状态仅与现在状态及其转移概率有关，而与以前状态无关，即无后效性。马尔科夫链进行的是区间预测，以区间划分系统状态，对于数据量较大的情形预测准确度较高。根据传染病历年的发病率资料建立马尔科夫预测模型，便能够实现对未来传染病的发病率进行预测〔34〕。

(4)灰色系统理论

灰色系统理论是我国学者邓聚龙教授于1982年创立的，在传染病的预测领域，应用最广泛的是灰色动态模型。灰色动态模型的思想是将无规律的原始数据变成较有规律的生成数据后再建立模型方程，并以此预测未来的发展趋势。

(5)逐步判别模型

逐步判别模型的原理与判别分析相同，即通过一批分类明确的训练样本，制定出判别标准对以后新的样本进行分类。李时习〔35〕选用近10年湖南省的月均气温、降雨量、日照时问等气象资料和钩体病发病率资料，构建了判别方程，将钩体病发病率按高低划分为若干个等级，利用气象资料对钩体病发病率等级进行判别预测，回代符合率为61.53%。

小 结

能够用于传染病流行趋势预测的统计学方法很多，但是没有一种方法能够适用于所有疾病的监测数据，因为每一种疾病和每一个监测系统都有其独特的特征〔36〕。相对于对统计模型的依赖，异常的探测更加依赖于监测系统的特征比如数据收集、监测系统的报告机制及其稳定性以及反应机制。因此，在分析系统数据之前，必须熟悉监测系统的结构，选择最合适的方法。

1.WHO，CSR.WHO recommended surveillance standards.1999.

2.CDC.http：//www.cdc.gov/ncphi/disss/nndss/phs/infdis2009.htm.available in 2009/11/05.

3.Besag J，Newell J.The detection of clusters in rare diseases.Journal of the Royal Statistical Society，1991，Series A(154)：143-155.

4.Kulldorff M.Statisticalmethods for spatial epidemiology：tests for randomness.GIS and Health，1998：49-62.

5.Tango T.Comparison of general tests for spatial clustering.In：Lawson et al(Eds).Disease Mapping and Risk Assessment for Public Health，1999.

6.Turnbull BW，Iwano EJ，Burnett WS，et al.Monitoring for clusters of disease：Application to leukem ia incidence in upstate New York.American Journal of Epidemiology，1990，132：136-143.

7.Tango T.A test for spatial disease clustering adjusted for multiple testing.Statist.Med，2000，19：191-204.

8.Kulldorff M.A spatial scan statistic.COMMUN.STATIST.-THEORY METH，1997，26(6)：1482-1496.

9.Tango T，Takahashi K.A flexibly shaped spatial scan statistic for detecting clusters.International Journal of Health Geographics，2005，4(11).

10.Bonetti M，Pagano M.Proceedings of the Biometrics Section on detecting clustering.American Statistical Association，2001：24-33.

11.Cuzick JR.Edwards.Spatial clustering for inhomogeneous popluations.Journal of the Royal Statistical Society，1990，Series B(52)：73-104.

12.Moran PAP.Notes on continuous stochastic phenomena.Biometrika，1950，37：17-23.

13.Oden N.Adjusting Moran's I for population density.Statistics in Medicine，1995，14：17-26.

14.Mantel N.The detection of disease clustering and a generalized regression approach.Cancer Research，1967，27：209-220.

15.Norstrom M，Pfeiffer DU，Jarp J.A space-time cluster investigation of an outbreak of acute respiratory disease in Norwegian cattle herds.Preventative Veterinary Medicine，2000，47：107-119.

16.Stroup DF，W illiamson GD，Herndon JL，et al.Detection of aberrations in the occurrence of notifiable diseases surveillance data.Statistics in Medicine，1989，8：323-329.

17.W illiamson GD，Hudson GW.A monitoring system for detecting aberrations in public health surveillance reports.Statistics in Medicine，1999，18：3283-3298.

18.Stern L，Lightfoot D.Automated outbreak detection：a quantitative retrospective analysis.Epidemiology and Infection，1999，122：103-110.

19.严薇荣.传染病预警指标体系及三种预测模型的研究.华中科技大学博士学位论文，2008.

20.吴家兵，叶临湘，尤尔科.ARIMA模型在传染病发病率预测中的应用.数理医药学杂志，2007，20(1)：90-92.

21.冯丹，韩晓娜，赵文娟等.中国内地法定报告传染病预测和监测的ARIMA 模型.疾病控制杂志，2007，11(2)：140-142.

22.吴家兵，叶临湘，尤尔科.时间序列模型在传染病发病率预测中的应用.中国卫生统计，2006，23(3)：276.

23.Goldenberg A，Shmueli G，Caruana RA，et al.Early statistical detection of anthrax outbreaks by tracking over-the-counter medication sales.Proceedings of the National Academy of Sciences，2002，99：5237-5249.

24.Lazarus R，Kleinman K，Dashevsky I，et al.Use of automated ambulatory-care encounter records for detection of acute illness clusters，including potential bioterrorism events.Emerging Infectious Diseases，2002，8：753-760.

25.Leonhard H，Giusi G，Christina F，et al.Joint spatial analysis of gastrointestinal infectious diseases.Statistical Methods in Medical Research，2006，(15)：465-480.

26.沈壮，黄若刚，腾仁明.GIS系统在卫生防病应急处理工作中的应用.中国公共卫生管理，2003，19(1)：24-25.

27.戚晓鹏，吕繁，何武.地理信息系统在流行病学中的应用及开发.中华流行病学杂志，2004，25(11)：997-999.

28.Kleinman K，Lazarus R，Platt R.A generalized linear mixed models approach for detecting incideng clusters of disease in small areas，with an application to biological terrorism.American Journal of Epidemiology，2004，159：217-224.

29.Rogerson P，Yamada I.Monitoring change in spatial patternsof disease：comparing univariate and multivariate cumulative sum approaches.Statistics in Medicine，2004，23：2195-2214.

30.Raubertas RF.An analysis of disease surveillance data that uses geographic locations of the reporting units.Statistics in Medicine，1989，8：267-271.

31.刘巧兰，李晓松，冯子健，等.Rogerson空间模式监测方法在传染病实时监测中的应用.中华流行病学杂志，2007，28(11)：1133-1137.

32.Altmann M.Susceptible-infected-removed epidemic models with dynamic partnerships.JMath Biol，1995，33(6)：661-75.

33.向立富.模糊综合评判法在流脑预测中的应用.中国卫生统计，1994，11(4)：33-34.

34.付长贺，邓甦.马尔科夫链在传染病预测中的应用.沈阳师范大学学报(自然科学版)，2009，27(1)：28-30.

35.李时习.逐步判别对钩端螺旋体病发病率的拟和与预测.实用预防医学，1998，5：120-121.

36.胡世雄，邢慧娴，邓志红.我国传染病的预测预警现状.中国预防医学杂志，2007，41(5)：407-410.