年龄调整率的区间估计及其在宫颈癌患病率估计中的应用*

魏永越 荀鹏程 余小金 赵 杨 李 瑛 张春延 于 浩 张肖敏△ 陈 峰△

年龄调整率的区间估计及其在宫颈癌患病率估计中的应用*

魏永越1荀鹏程1余小金1赵 杨1李 瑛2张春延3于 浩1张肖敏3△陈 峰1△

目的评价三种年龄调整率可信区间估计方法，探索适合江苏省宫颈癌筛查研究中年龄调整患病率可信区间估计的方法。方法 以二项分布正态近似法、Gamma分布法及“确切概率法”进行年龄调整率的区间估计，运用统计模拟考察多种率及阳性数情况下三种方法的区间覆盖率及宽度。结果 当样本量较小(阳性数较少)时，确切概率法的覆盖率离理论可信度的偏差及区间宽度均优于Gamma分布法，两者的覆盖率均明显优于正态近似法;随着阳性数增多，三法各自的覆盖率偏差及区间宽度均逐渐变小，方法间的差异亦逐渐缩小;当阳性数增至30以上时，确切概率法及正态近似法的覆盖率的偏差皆在±1%以内，此时两者的区间宽度接近;而Gamma分布法的覆盖率偏差若要达到1%以内，则要求总阳性数在100以上。无论样本构成是轻度偏离还是明显偏离总体构成，上述规律皆成立。结论 综合考虑区间覆盖率、区间宽度及计算便捷性，建议当总阳性数小于30时，采用确切概率法计算调整率的可信区间;当总阳性数大于等于30时，采用正态近似法。

年龄调整率 正态近似法 Gamma分布法 确切概率法

*：江苏省科技支撑计划(社会发展)项目资助(基金编号BS2007080)

1.南京医科大学流行病与卫生统计学系(210029)

2.江苏省计划生育科学技术研究所(210036)

3.江苏省人口和计划生育委员会(210008)

△通信作者：陈峰，E-mail：FengChen@njmu.edu.cn;张肖敏，E-mail：zhangxiaominjs@126.com

年龄调整的患病率是消除抽样调查中年龄构成偏离该地区实际人口构成所造成的影响而计算的一种“标化率”。用于标化的标准人口构成一般为样本所对应的总体的人口构成，此时年龄调整率为相应总体患病率的估计值，其在流行病学研究中应用广泛。如何计算年龄调整率的可信区间是学术界所关注的问题。Chiang于1961年阐述了年龄调整患病率的方差估计方法并基于正态近似法估计年龄调整率的可信区间〔1〕，该法目前较为常用;Fay等于1997年建立了基于Gamma分布的可信区间算法〔2〕，美国华盛顿州卫生部门(Washington State Department of Health)于2002年推荐此法〔3〕;还有一些基于 beta分布的计算方法〔4〕。由于上述方法的应用条件不是十分明确，实际运用中难以把握。尤其是在患病率较低、总阳性数较少的情况下，上述几种方法的估计效果尚未考证。因此，本文针对某省2006年宫颈癌筛查数据，在计算年龄调整的宫颈癌患病率时，对正态近似法、Gamma分布法，以及笔者提出的“确切概率法”加以考察、比较，以探索适合于该类资料的估计方法以及三种方法的应用条件。

方法原理

记N为总人口数，ni为样本中第i个年龄组的调查人数，pi表示第i个年龄组的患病率，ci表示标准人口第i个年龄组的构成，则年龄别调整率为

下文介绍三种方法用于估计其可信区间。

1．正态近似法 目前此法较为常用〔1〕，其可信度为1-α的可信区间为：

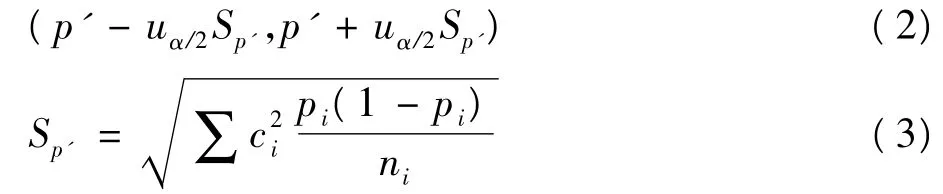
其中，uα/2为标准正态分布下，右侧累积概率为α/2时的界值，Sp'为p'的标准误。

2．Gamma分布法 Fay等提出基于Gamma分布的方法估计年龄调整率的可信区间〔2〕，计算方法如下：

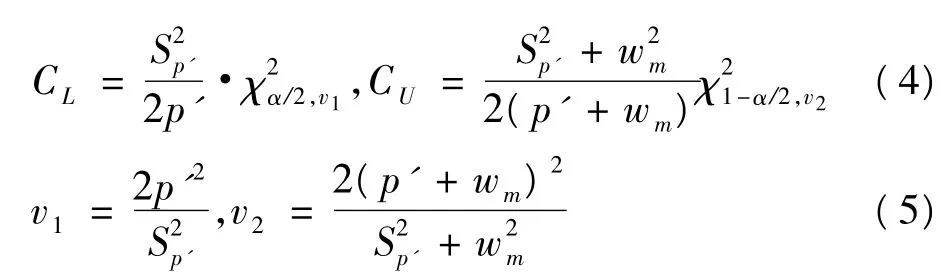
式中，Sp'即正态近似法中计算的年龄调整率的标准误为自由度为v、左侧累积概率为α时的卡方界值，wm=max(ci/ni)。

3．确切概率法 如果阳性数很少，采用正态近似效果较差，则应使用确切概率法计算率可信区间。基于此我们提出年龄调整率的确切概率法，步骤如下：第一步，计算年龄调整率：p'=∑cipi。第二步，计算理论阳性数：r=Round(N·p')，Round(x)为四舍五入函数。第三步，基于总样本含量N及阳性数r，采用传统的确切概率法计算调整率的可信区间。确切概率法计算单个率的可信区间，算法如下：

Clopper＆Pearson于1934年基于二项分布，采用逐步搜索法求解单个率的可信区间，称为确切概率法〔5〕，New combe等研究认为该方法具有很好的覆盖率及估计精度〔6〕。令n为样本含量，r为阳性数，1-α为可信度，CL为可信区间下限，CU为上限，则须满足：

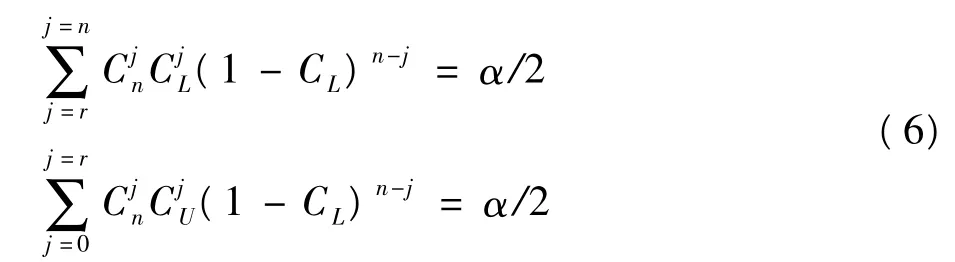
不难理解，对于可信区间下限CL，即是Beta分布Beta(r，n-r+1)中左侧累积概率为α/2的值，上限CU，即是Beta分布Beta(r+1，n-r)中左侧累积概率为1-α/2的值。即：

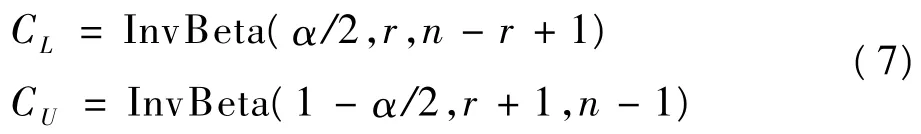
其中“InvBeta(p，r，n-r)”为 Beta分布的逆分布函数，即Beta(r，n-r)中左侧累积概率为p时的值。在SAS、Stata、R等统计软件中，即基于此算法计算率的确切法可信区间。

M iettinen〔7〕在此基础上，根据Beta分布与F分布的关系，推导得可信区间上下限的计算公式：

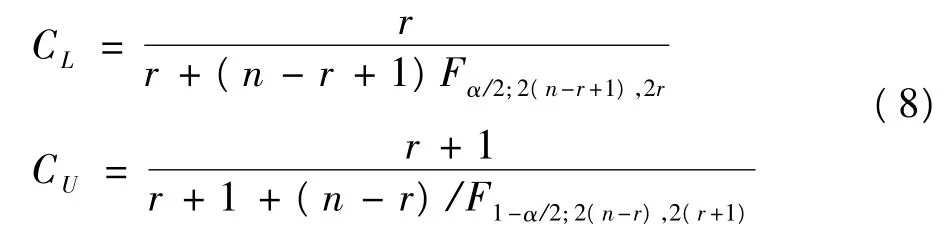
其中n为样本含量，r为阳性数，1- α为可信度，Fα;v1，v2为F分布中左侧累积概率为α，第一、二自由度分别为ν1、ν2时的F值。所得CL和CU即为确切概率法可信区间的下限和上限。

实例分析

宫颈癌是最常见的妇科恶性肿瘤，是严重威胁妇女健康的一种疾病，患病率居我国女性生殖系统恶性肿瘤的首位。我国自解放以来，宫颈癌的普查和筛查工作陆续在全国各地广泛开展。本文资料来自以某省已婚妇女宫颈癌筛查技术规范及人群随访研究课题2006年的调查数据，评价三种方法对年龄调整率可信区间的估计效果。

2006年共筛查已婚育龄妇女40 459例，合格样本40 399例。首先，对每位受访者进行细胞学检查(宫颈粘液的巴氏图片检查);其次，对细胞学检查阳性者进行宫颈组织病理切片检查，仍为阳性者则确诊为宫颈癌。共527例细胞学检查阳性，确诊病例35人，粗患病率为86.77/10万。各年龄组人数、患病情况及标化患病率的计算见表1。标准人口构成来自该省2005年人口1%抽样调查35～65岁年龄组女性分布资料〔8〕，年龄调整患病率为88.90/10万。采用正态近似法、Gamma分布法及确切概率法分别计算年龄调整患病率的95%可信区间见表2。

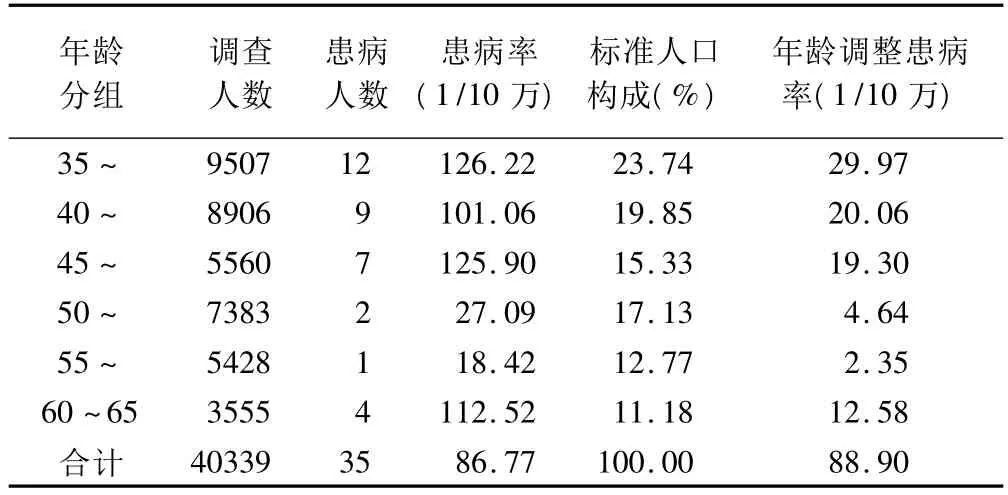
表1 各年龄组宫颈癌患病率及年龄调整患病率(1/10万)的计算

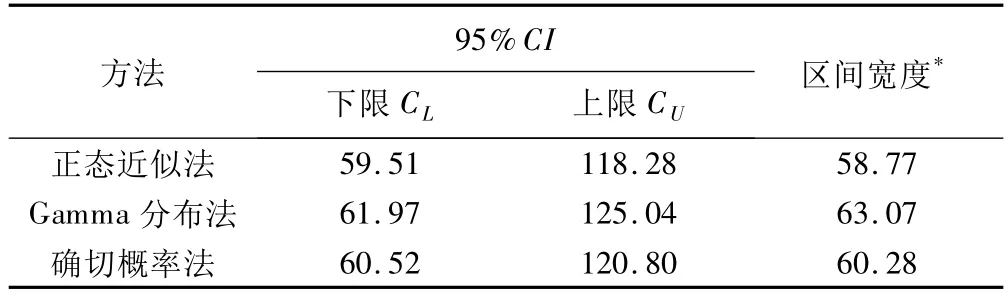
表2 宫颈癌筛查年龄调整患病率的区间估计(1/10万)

方法比较

采用计算机模拟比较三种方法对该类型实际资料的估计效果，以及考察不同患病率水平、不同阳性数情况对三种方法估计效果的影响。模拟试验一是以上述宫颈癌筛查数据为例，在总体患病率不变的情况下，比较不同样本含量(阳性数)对三种方法估计结果的影响;模拟试验二探讨当样本构成与总体人口构成差异不大时，在不同率的水平、样本含量组合对三种方法估计结果的影响;模拟试验三探讨当样本构成与总体人口构成差异明显时，在不同率的水平、样本含量组合对三种方法估计结果的影响。

1.模拟试验一 以上述资料患病率为实际背景，设计计算机模拟试验如下：

(1)以上述宫颈癌筛查数据为例，设置总患病率(88.90/10 万)，总阳性数分别为 1，5，10，15，20，…，120，据此可计算总样本量。

(2)年龄组、样本年龄构成以及各年龄组的阳性率同本资料，由此计算各年龄组样本量;

(3)利用二项分布原理，在各年龄组内随机产生实际发生的阳性数;

(4)以2005年江苏省1%人口抽样调查35～65岁女性年龄构成为标准人口构成，采用三种方法计算年龄调整率的可信区间;该步骤重复20000次，并评价各方法的区间覆盖率(区间包含参数的比例)及平均宽度。

模拟结果显示，当总阳性数较少时，正态近似法区间覆盖率明显低于95%，Gamma分布法及确切概率法的覆盖率皆高于95%，但后者的覆盖率偏差最小;随着样本含量的增加，三种方法的区间覆盖率逐渐接近理论可信度;总阳性数大于等于15时，确切概率法的覆盖率偏差降至±1%之内;当总阳性数大于25时，正态近似法的覆盖率偏差亦降至±1%之内;而Gamma分布法的覆盖率偏差若要达到1%以内，则要求总阳性数在100以上。

对于区间宽度而言，当阳性数较少时，正态近似法的区间宽度明显小于其余两法，Gamma分布法的区间最宽;随着样本含量的增加，区间宽度逐渐减小，三种方法之间的差别亦逐渐缩小;当总阳性数较大时，正态近似法与确切概率法的区间宽度差异很小，Gamma分布法的区间宽度始终略大于其余两者。

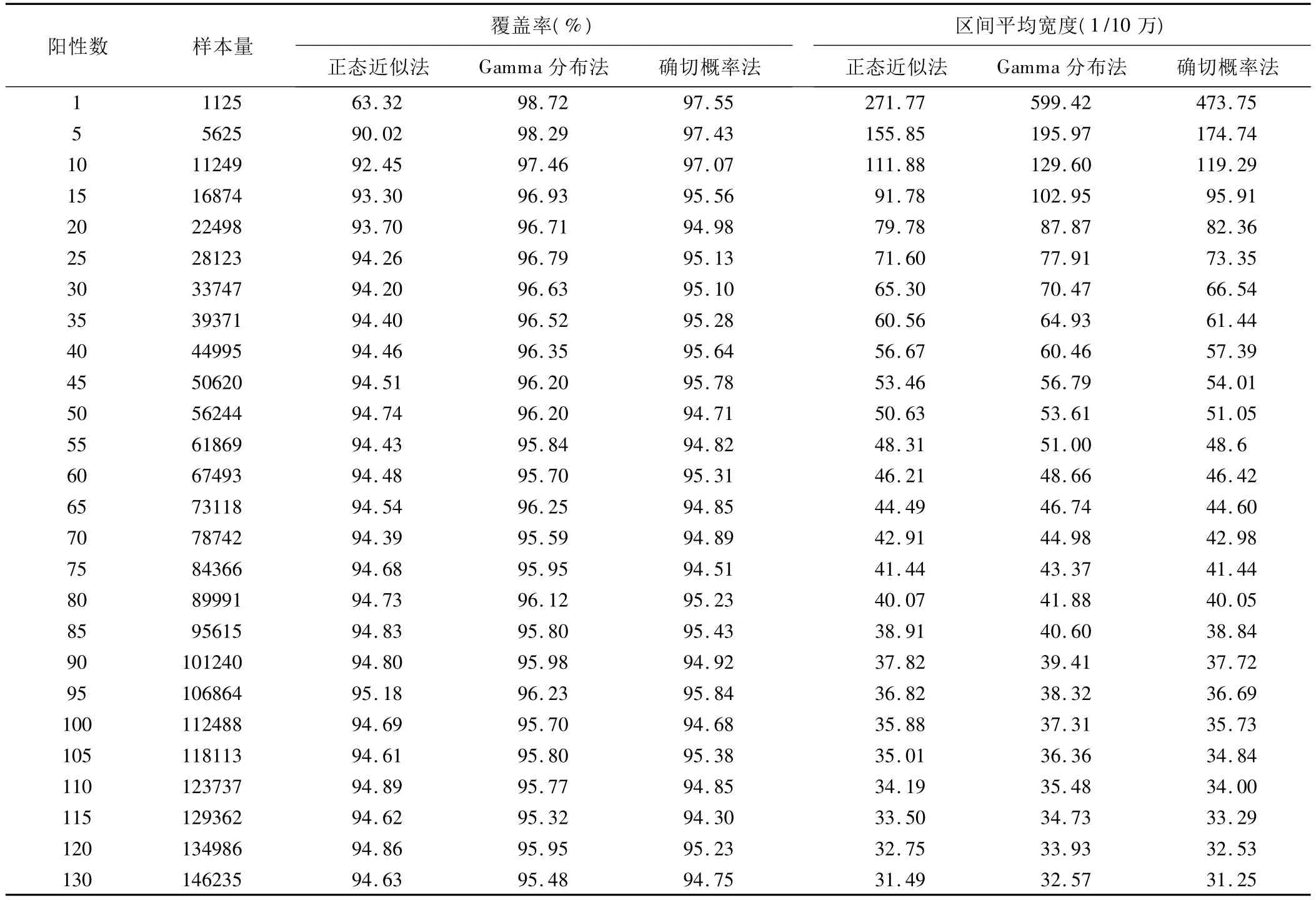
表3 不同阳性数情况下三种方法覆盖率与区间宽度(模拟试验一)

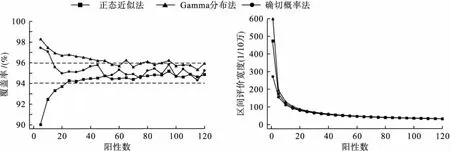
图1 三种方法区间覆盖率、区间宽度随合计阳性数的变化情况(模拟试验一)

2.模拟试验二 通过模拟试验考察当样本人口构成与总体人口构成稍微偏离时，不同率的情况下样本含量对三种方法估计结果的影响，试验设置如下：

(1)参照宫颈癌筛查的实际资料设置样本年龄组及年龄别构成，仍以江苏省2005年1%人口抽样调查35～65岁女性年龄构成作为总体年龄别构成;

(2)总体患病率π依次设为1/10万、5/10万、1/万、1/‰、1%、5%、10%等7个水平，并假设年龄组间患病率环比下降20%，计算各年龄组的患病率πi;

(3)各总体率情况下，合计阳性数r设为1，5(5)45等不同情况，计算各参数组合下所需总样本含量：n=r/π，并计算各年龄组的样本量ni;

(4)根据各年龄组的样本量ni及期望患病率πi，基于二项分布原理随机产生实际发生的阳性数xi;

(5)采用三种方法计算年龄别调整率的95%可信区间;

(6)各总体患病率条件下重复抽样20000次，评价各方法的区间覆盖率及平均宽度。

模拟结果显示，不同患病率情况下，总阳性数对区间覆盖率及宽度的影响规律一致。当患病率很低时，正态近似法区间覆盖率明显低于95%，Gamma分布法及确切概率法的覆盖率皆高于95%，后者的覆盖率偏差最小;随着样本含量的增加，三种方法的区间覆盖率逐渐接近理论可信度，区间宽度亦逐渐减小;当总阳性数大于30时，正态近似法及确切概率法覆盖率与理论可信度的偏差在±1%之内，而Gamma分布法的偏差相对较大，此时区间宽度：正态近似法 ≤确切概率法＜Gamma分布法。

3.模拟试验三 通过模拟试验考察当样本人口构成与总体人口构成明显偏离时，不同率的情况下样本含量对三种方法估计结果的影响，模拟试验如下：

(1)年龄组设置宫颈癌筛查资料，年龄构成设置为均匀分布(即各年龄组的样本构成比为16.67%)，仍以江苏省2005年1%人口抽样调查35～65岁女性年龄构成作为总体年龄别构成;

(2)总体患病率π及各年龄组患病率设置同模拟试验二;

(3)合计阳性数r及各年龄组样本量设置同模拟试验二;

(4)各年龄组的实际发生的阳性数xi的产生方法、模拟次数及方法评价指标同模拟试验二。

模拟结果显示，当样本人口构成与总体人口构成明显偏离时，总体患病率及总阳性数对区间覆盖率及宽度的影响规律同模拟试验二基本一致。

讨 论

本文所提方法仅适用于计算非传染性疾病的患病率的年龄别调整率。当阳性数很少或率很低时，率的抽样分布与正态分布相差较远，因此若采用正态近似法计算率的可信区间，将导致较大误差，覆盖率将明显下降。Fay等〔2〕人认为当阳性数很少时用Gamma分布法得到的年龄调整率的可信区间较之正态近似法合理，Brillinger〔9〕认为当阳性数较多时得出的区间接近于传统的正态近似法。

调整率的本意是为了构成不同的样本率之间的比较，但当以调查样本相应总体的年龄构成作为标准年龄构成时，年龄别调整的患病率实为相应总体患病率的无偏估计：假设某有限总体，总体率为π，该总体按照年龄分为k层，每层相应的构成比为ci，总体率为πi，该总体包含N个个体，每层包含ni个个体。则π=∑niπi/N=∑ciπi。从该总体中随机抽样，样本含量为N'，每层样本量为n'i，每层的样本构成比为c，样本率为pi。纵使样本构成与总体构成ci有非常明显的差异，各年龄层的样本率pi都应该是πi的无偏估计，即表示为。按照年龄调整率的公式pc=∑cipi=∑cii，即可知样本年龄调整率pc为相应总体率π的无偏估计。此时，年龄调整患病率的可信区间实为相应总体的患病率的可信区间。因此基于总样本含量及年龄调整率，采用确切概率法计算调整率的可信区间是合理的。从模拟结果来看，用确切概率法计算非传染性疾病的患病率的年龄别调整患病率的可信区间是可行的。

当样本人口构成轻度偏离标准人口构成时，不同的率情况下，阳性数情况对三种方法区间估计效果的影响规律基本一致。阳性数较少时，确切概率法最优;随着阳性数的增大，方法间的差异亦逐渐缩小;当阳性数增至30以上时，正态近似法及确切概率法的覆盖率的偏差皆在±1%以内，两者的区间宽度接近，皆优于Gamma分布法。模拟试验三显示，当样本人口构成明显偏离标准人口构成时，此规律依旧。

本研究亦显示，三种方法覆盖率偏差的收敛速度不同，依次为：确切概率法＞正态近似法＞Gamma分布法。若要求覆盖率偏差在±1%以内，则确切法要求总阳性数在15以上，正态近似法要求30例以上，而Gamma分布法则要求总阳性数在100以上。为了验证该规律的稳定性，增加模拟试验考察率为1‰、1%情况下，不同阳性数对结果的影响，结果亦呈现相似的规律。

综合考虑区间估计的准确度、精确度及计算的便捷性，建议当阳性数小于30时，采用本文提出的确切概率法计算年龄调整率的可信区间;当阳性数大于等于30时，采用正态近似法。本文采用计算机模拟探讨了几种不同条件下三种调整率可信区间估计的统计学性质，虽然模拟的参数组合不能覆盖所有实际情况，但仍有一定的代表性。

1.Chiang CL.Standard error of the age-adjusted death rate.Vital Statistics Special Reports：selected studies，1961，47(9)：271-285.

2.Fay MP，Feuer EJ.Confidence intervals for directly adjusted rates：a method based on the gamma distribution.Stat Med，1997，16：791-801.

3.Washington State Departmentof Health.Guidelines for Using Confidence Intervals for Public Health Assessment，2002：4-5.Available at http：//www.doh.wa.gov/data/guidelines/ConfIntguide.htm.

4.Ram CT，Clegg LX，Zou Z.Efficient interval estimation for age-adjusted cancer rates.Statistical Methods in Medical Research，2006，15：547-569.

5.Clopper CJ，Pearson ES.The use of confidence or fiducial lim its illustrated in the case of the binom ial.Biometrika，1934，26：404-413.

6.Newcombe RG.Two-sided confidence intervals for the single proportion：comparison of seven methods.Stat Med，1998，17(8)：857-872.

7.Miettinen OS.Estimation of relative risk from individually matched series.Biometrics，1970，26：75-86.

8.江苏省统计局.江苏省2005年人口年龄构成情况(2005年1%人口抽样调查资料).江苏统计年鉴—2006(电子版).http：//www.jssb.gov.cn/jstj/jsnj/2006/nj03.htm.

9.Brillinger DR.The natural variability of vital rates and associated statistics.Biometrics，1986，42：693-734.

Interval Estimation of Age-adjusted Rate and its App lication in Estimation for Cervix Cancer Prevalence

WeiYongyue，XunPengcheng，YuXiaojin，etal．DepartmentofEpidemiology＆Biostatistics，SchoolofPublicHealth，NanjingMedicalUniversity(210029)，Nanjing

ObjectiveTo evaluate three estimation methods of confidence interval for age-adjusted prevalence，i.e.method based on normal approximation to binomial distribution，gamma distribution method and exact probability method，and propose an appreciate method in efficient interval estimation for age-adjusted cervix cancer prevalence.Methods Statistical simulation was conducted to evaluate three interval estimation methods for age-adjusted prevalence based upon large-scale screen data for cervix cancer by comparing coverage rate and average interval width.ResultsW ith small sample size，the coverage rate and interval width for exact probability method was superior to the gamma distribution method，and both these two methods were apparently superior to the normal approximation method.When the sample size becomes large，the coverage deviations and interval widths were both shrink.With the total positive number greater than 30，the coverage deviations of the methods based on normal approximation and exact probability method was less than 1%，and the difference of the interval widths of these two methods is negligible.Meanwhile，the Gamma distribution method needed more positive numbers(more than 100)to make the coverage deviation less than 1%.This rule was stable regardless the degree of the difference between the proportion of random sample and population.ConclusionAccording to the coverage rate，interval width and convenience of calculating，the exact probability method is recommended when the total positive number is less than 30，while the method based on normal approximation to binomial distribution is proposed when the total positive number is equal or greater than 30.

Age-adjusted rate;Normal approximation to binom ial distribution;Gamma distribution;Exact probability