基于多尺度线调频基稀疏信号分解的包络阶次谱在齿轮故障诊断中的应用

皮 维 于德介 彭富强 罗洁思

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于多尺度线调频基稀疏信号分解的包络阶次谱在齿轮故障诊断中的应用

皮 维 于德介 彭富强 罗洁思

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

提出了基于线调频基稀疏信号分解的包络阶次谱方法，并将其应用于变速齿轮箱故障诊断之中。采用基于多尺度线调频基的稀疏信号分解得到齿轮箱啮合分量的瞬时频率，由此得到转速信号，并据此对齿轮振动加速度信号的包络信号进行等角度重采样，然后对重采样信号进行频谱分析，得到包络阶次谱，从而进行齿轮故障诊断。该方法无须使用转速计拾取转速信号，用软件方法实现了包络阶次分析，仿真算例与应用实例说明了该方法的有效性。

稀疏信号分解；包络阶次谱；齿轮；故障诊断

0 引言

在旋转机械故障诊断的工程实际中，往往存在变转速工况。风力发电机受非平稳空气动力载荷而变转速运行时，其旋转部件（如齿轮或轴承）产生的振动和噪声特征与轴的转速密切相关［1］。对于变转速工况下的旋转机械，以等时间间隔采样得到的振动信号一般为非平稳信号，传统方法无法有效提取其故障信息。例如，对变转速齿轮箱振动信号进行包络谱分析不能有效提取其随转速变化的故障信息［2－3］。

阶次谱分析采用等角度采样［4－5］，采样信号具有角度域的平稳性，因此适用于变转速工况下的旋转机械故障振动信号分析。阶次分析一般分为硬件方法和软件方法，硬件方法需要使用角度编码盘、跟踪滤波器和转速计等硬件，软件方法通过内插算法和鉴相装置实现角度重采样，比硬件方法更容易实现且成本较低。但软件方法仍要使用鉴相装置进行转速跟踪，由于受限于硬件的安装环境，其应用范围有限［6－7］。

基于多尺度线调频基的稀疏信号分解［8］结合Mallat等［9］提出的稀疏信号分解与 Candès等［10］提出的线调频小波路径追踪算法，得到瞬时频率具有物理意义的单分量信号。本文提出一种适用于变速齿轮箱故障诊断的包络阶次谱方法。该方法利用基于多尺度线调频基的稀疏信号分解得到齿轮箱振动信号啮合分量的瞬时频率，将瞬时啮合频率除以齿轮齿数得到瞬时转频，再对原始信号进行包络分析，然后依据估计的转速信号对该包络信号进行角度重采样得到角域平稳信号，最后通过FFT获得相应阶次谱来诊断齿轮箱故障。本文方法通过信号分解得到的啮合分量的瞬时频率来估计转速信息，进而实现包络阶次谱分析，克服了一般阶次分析方法受限于硬件安装环境的不足。仿真算例与应用实例表明，本文方法能有效应用于转速波动下齿轮箱的故障诊断。

1 基于多尺度线调频基的稀疏信号分解

定义多尺度线调频基函数库为

计算在每一动态分析时间段I上具有最大投影系数的基元函数，时间段I内的最大投影系数计算公式为

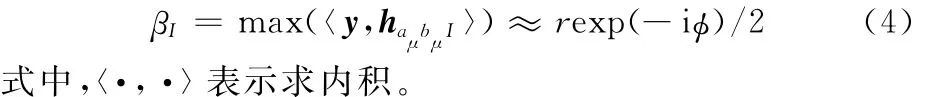
利用这组基元函数来对y（t）进行分解，该组基元函数的支撑区应该覆盖整个分析信号，且不重叠，则在时间段I内βI所代表的分解信号为

根据线调频小波路径追踪算法，采用合适的动态分析时间段连接方法可以使分析信号的残余信号能量最小［10］，得到的分解信号总能量最大，即

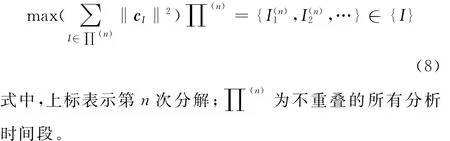
将第一次分解的残余信号作为下轮分解的分析信号再分解，以此方法逐次分解残余信号，直到残余信号能量小于一定的阈值后停止。

选择分析尺度j的变化范围，利用多尺度的基元函数对时频面的时间轴进行划分，每一动态时间段I内基元函数的瞬时频率为aμ＋2bμt，能在小的动态分析时间段内逐段线性拟合呈曲线变化的频率分量，因此该方法得到的是瞬时频率具有物理意义的单分量信号。

2 基于多尺度线调频基稀疏信号分解的包络阶次谱

恒定转速工况下，齿轮发生集中或分布性故障，对其振动加速度信号进行频谱分析时，通常会出现以齿轮的啮合频率为中心频率、以齿轮所在轴的转频或其高次倍频为调制频率的调制边频带［12］。然而当转速波动时，调制边频带将会“模糊”，而基于多尺度线调频基稀疏信号分解的包络阶次谱方法可以提取轴的瞬时转频，并对分析信号的包络信号进行等角度重采样，进而将时域非平稳信号转换为角域平稳信号，满足FFT分析对信号平稳性的要求，有效解决“频率模糊”问题。

基于多尺度线调频基稀疏信号分解的包络阶次谱方法具体实现步骤如下：

（1）由基于多尺度线调频基的稀疏信号分解齿轮振动加速度信号得到齿轮啮合分量的瞬时频率，从而得到其瞬时转频f（t），用三阶多项式拟合，有

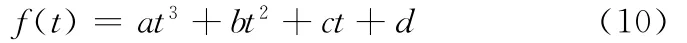
（2）确定阶次跟踪的最大分析阶次Mmax。

（3）根据采样定理，采样率至少应为最大分析阶次的两倍，所以有

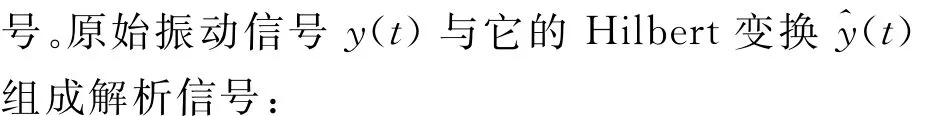
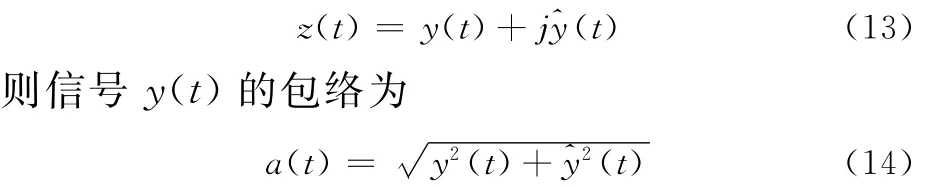
（6）根据已求出的tn值，对包络信号a（t）进行插值，求出其对应于时间点tn的幅值，得b（tn）。

（7）对重采样信号b（tn）进行FFT变换得到信号的包络阶次谱。

3 仿真信号分析

为验证本文方法的有效性，按照式（15）的齿轮振动信号模型对一仿真信号进行分析。假设齿轮齿数为10，齿轮故障仿真信号为

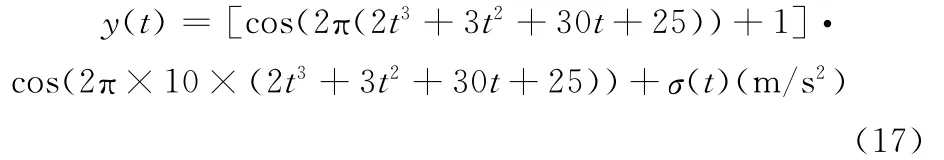
图1所示为未加噪声时的调幅调频仿真信号时域波形。图2所示为加高斯白噪声σ（t）后的调幅调频仿真信号时域波形，信号信噪比为0，噪声能量与调幅调频信号能量相等。由于白噪声的影响，从图2中无法分辨出调幅调频信号。

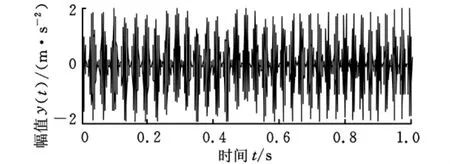
图1 调幅调频仿真信号

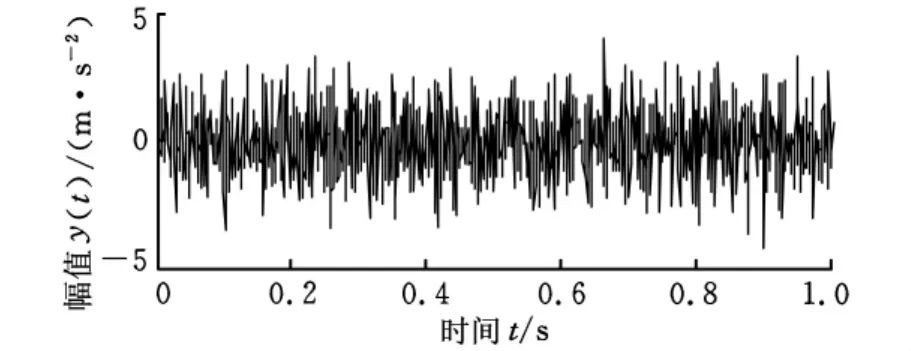
图2 加噪后的调幅调频仿真信号

仿真信号分析中采样频率为1000Hz，采样点数为1024点。选择合适的分解参数，利用基于多尺度线调频基的疏信号分解对仿真信号进行分解，得到啮合分量的瞬时频率如图3a所示，并由式（12）得到瞬时转频如图3b所示。

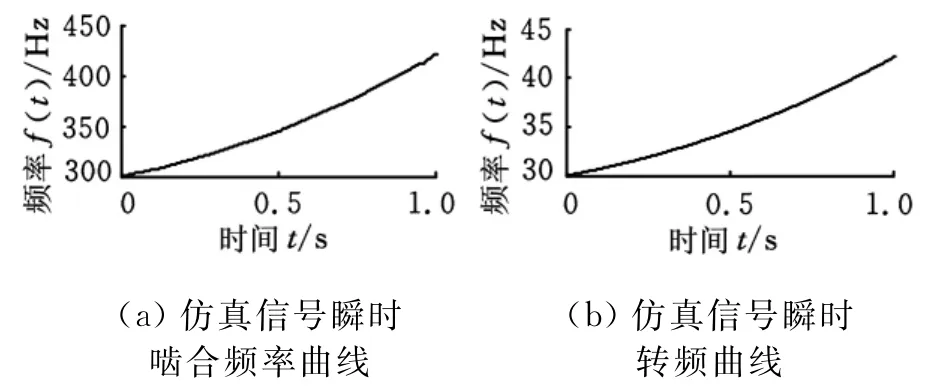
图3 仿真信号瞬时频率曲线

采用三阶多项式拟合瞬时转频得

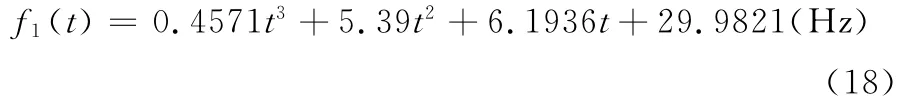
对仿真信号进行Hilbert变换，求得其包络信号，利用f1（t）对包络信号进行等角度重采样，最大分析阶次Dmax取20，然后进行FFT变换，得到仿真信号的包络阶次谱如图4所示。从图4中可以看出，在阶次为1.035处有明显峰值，对应着齿轮的转频，说明仿真信号被转频成分幅值调制，与式（17）的假设相符。基于多尺度线调频基稀疏信号分解的包络阶次谱将信号的调制特征直观的表现出来，准确地提取和识别了齿轮故障特征，可以有效应用于非平稳转速下的齿轮故障诊断。

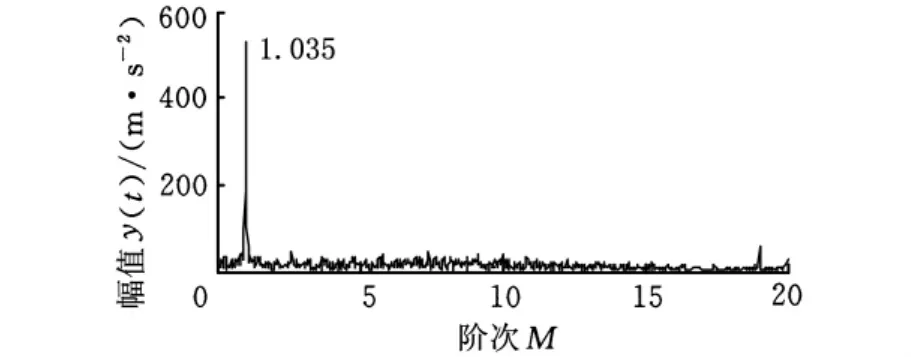
图4 仿真信号包络阶次谱

4 齿轮故障诊断实例

为进一步验证本文方法的有效性，分别对断齿、裂纹和正常齿轮的振动信号进行了分析。将齿轮箱故障试验台上的某一主动齿轮切割一个齿，模拟齿轮断齿故障，输入轴齿轮齿数为55，输出轴齿轮齿数为75。采集齿轮箱振动加速度信号，在非恒定转速下采集断齿齿轮信号和正常齿轮信号，其中正常齿轮和断齿齿轮参数相同。同时，为验证本文方法提取齿轮瞬时转频的有效性，采用光电转速计拾取断齿齿轮的转速信号。再用一对模数相等、齿数均为37的齿轮替换上述主从动轮，并将其某一齿根处激光切割深度约为1.5mm的裂纹模拟齿轮裂纹故障，在变转速下采集裂纹齿轮振动信号。试验采样频率为4096Hz，采样时长为2s。图5为断齿齿轮振动信号时域波形图。

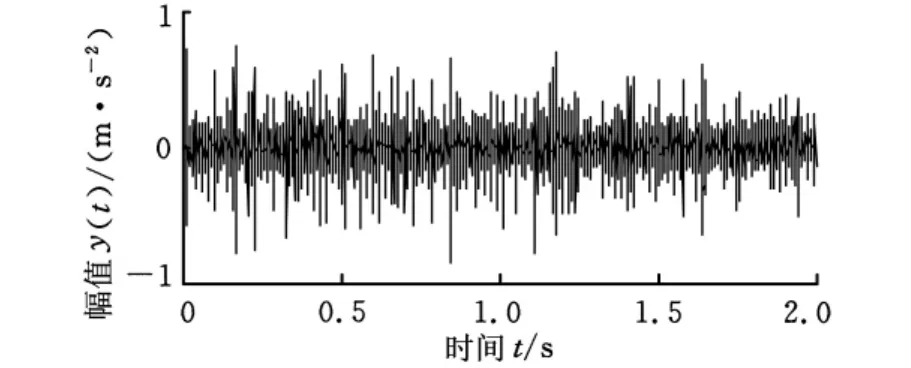
图5 断齿齿轮振动加速度信号

从图5的时域信号中可以看到冲击现象，但冲击的时间间隔不均匀，说明在转速波动下齿轮振动冲击信号具有非平稳性，对其进行FFT分析得到如图6所示频谱。

图6 断齿齿轮振动信号FFT频谱

从图6也无法识别调制信息，从而无法判断齿轮故障。

选择合适的分解参数，利用基于多尺度线调频基稀疏信号分解对断齿齿轮信号进行分解，得到的瞬时啮合频率如图7a所示，并由式（12）得到断齿信号的瞬时转频曲线如图7b所示。

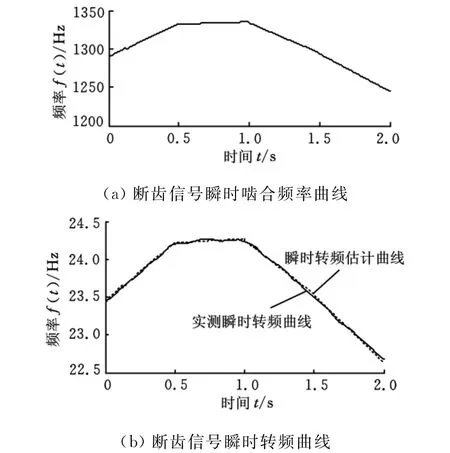
图7 断齿信号瞬时频率曲线

从图7b中看出，由瞬时啮合频率估计的瞬时转频曲线与实测瞬时转频曲线基本重合。

采用三阶多项式拟合瞬时转频得

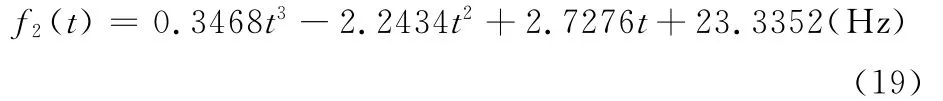
对断齿信号进行Hilbert变换，求得其包络信号，利用f2（t）对包络信号进行等角度重采样，最大分析阶次Dmax取20，然后进行FFT变换，得到断齿信号的包络阶次谱如图8所示。

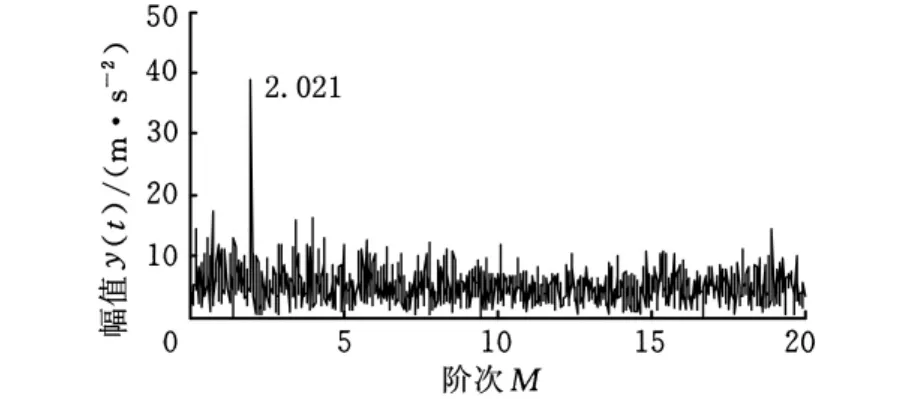
图8 断齿齿轮振动信号包络阶次谱

从图8中可以看出，在阶次为2.021处有明显峰值，对应着齿轮的2倍转频，说明断齿齿轮信号被2倍转频幅值调制，与断齿故障特征相符。

采用基于Reassigned smoothed pseudo Wigner－Ville峰值跟踪算法得到断齿振动信号的瞬时转频如图9所示。

图9 基于峰值跟踪算法估计转频

从图9a中得出，转频大致在20～30Hz之间波动，且时频图存在严重的毛刺现象。从图9b中可知，拟合估计转频得到的曲线与实测转频曲线无重合。对比图7b、图9b可以看出，基于多尺度线调频基稀疏信号分解估计瞬时转频的精度高于基于reassigned smoothed pseudo Wigner－Ville峰值跟踪的算法所得的瞬时转频的精度。

依据此转速信号对断齿信号进行重采样并得到其包络阶次谱如图10所示。

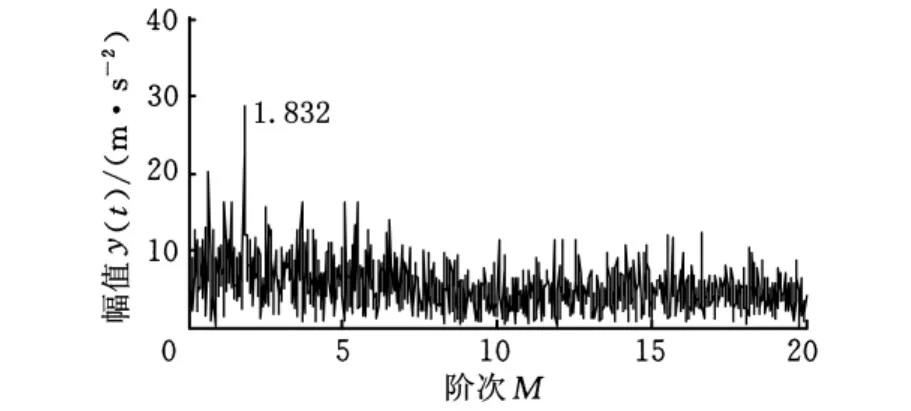
图10 基于reassigned smoothed pseudo Wigner－Ville峰值跟踪的包络阶次谱

对比图8、图10可以看出，基于多尺度线调频基稀疏信号分解的包络阶次谱比基于reas－signed smoothed pseudo Wigner－Ville峰值跟踪的包络阶次谱精度更高，前者能准确提取齿轮故障特征。

利用基于多尺度线调频基的稀疏信号分解得到裂纹齿轮信号瞬时转频为

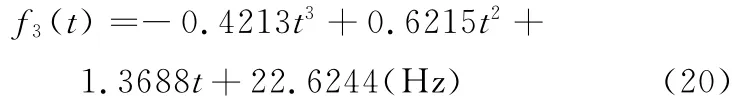
由此可求得裂纹齿轮信号的包络阶次谱如图11所示。从图11中可以看出，在阶次分别为1.032和2.021处有明显峰值，分别对应着齿轮的转频和2倍转频，说明裂纹齿轮信号被转频和2倍转频调制，与裂纹故障特征相符。

图11 裂纹齿轮振动信号包络阶次谱

同样可以得到正常齿轮的包络阶次谱如图12所示。从图12中无法找到与转频有关的明显阶次，即不具有在故障情况下齿轮啮合频率被转频或转频高倍频调制的特征。

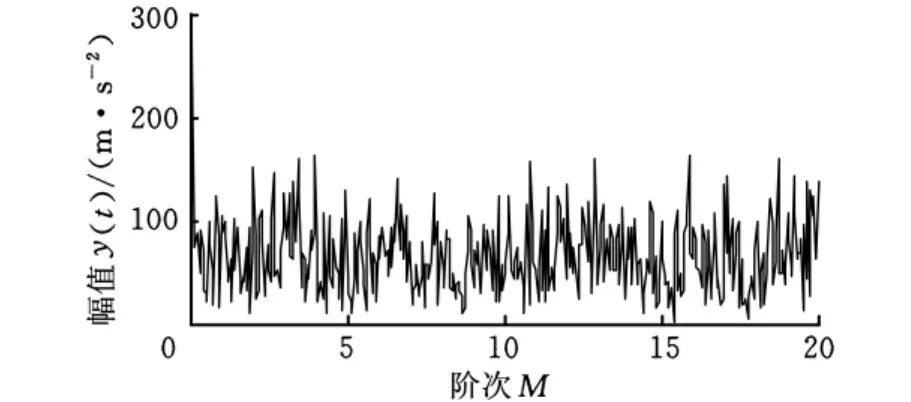
图12 正常齿轮振动信号包络阶次谱

5 结束语

本文利用基于多尺度线调频基稀疏信号分解的包络阶次谱方法分析调幅－调频信号，并将其应用于非平稳转速状态下的齿轮箱故障诊断中。仿真和实验结果表明：在不使用其他硬件设备辅助的情况下，基于多尺度线调频基稀疏信号分解的包络阶次谱方法能有效地提取齿轮振动信号中与转频相关的调幅特征，是一种有效的非平稳转速下齿轮故障诊断的新方法。

［1］ Lu Bin，Li Yaoyu，Wu Xin，et al.A Review of Recent Advances in Wind Turbine Condition Monitoring and Fault Diagnosis［J］.Power Electronics and Machines in Wind Applications，IEEE，2009，24－26：1－7.

［2］ Cheng Junsheng，Yang Yu，Yu Dejie.The Envelope Order Spectrum Based on Generalized Demodulation Time－Frequency Analysis and Its Application to Gear Fault Diagnosis［J］.Mechanical Systems and Signal Processing，2010，24（2）：508－521.

［3］ 杨宇，于德介，程军圣.基于经验模态分解包络谱的滚动轴承故障诊断方法［J］.中国机械工程，2004，15（8）：1469－1471.

［4］ Bossley K M，Mckendrick R J，Harris C J，et al.Hybrid Computed Order Tracking［J］.Mechanical Systems and Signal Processing，1999，13（4）：627－641.

［5］ Wu Jianda，Wang Yu Hsuan，Chiang Peng Hsin，et al.A Study of Fault Diagnosis in a Scooter Using Adaptive Order Tracking Technique and Neural Network［J］.Expert Systems with Applications，2009，36（1）：49－56.

［6］ 郭瑜，秦树人，汤宝平，等.基于瞬时频率估计的旋转机械阶比跟踪［J］.机械工程学报，2003，39（3）：32－36.

［7］ 孔庆鹏，宋开臣，陈鹰.发动机变速阶段振动信号时频分析阶比跟踪研究［J］.振动工程学报，2005，18（4）：448－452.

［8］ 彭富强，于德介，罗洁思，等.基于多尺度线调频基稀疏信号分解的齿轮故障诊断［J］.中国机械工程，2009，20（14）：1726－1730.

［9］ Mallat S，Zhang Z.Matching Pursuit with Time－Frequency Dictionaries［J］.Signal Processing，1993，41（12）：3397－3415.

［10］ Candès E J，Charlton P R，Helgason H.Detecting Highly Oscillatory Signals by Chirplet Path Pursuit［J］.Applied and Computational Harmonic Analysis，2008，24（1）：14－40.

［11］ Huang N E，Shen Z，Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proc.R.Soc.Lond.A，1998（454）：903－995.

［12］ 丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京：机械工业出版社，2005.

Application of Envelope Order Spectrum Based on Multi－scale Chirplet and Sparse Signal Decomposition to Gearbox Fault Diagnosis

Pi Wei Yu Dejie Peng Fuqiang Luo Jiesi
State Key Laboratory of Advanced Design and Manufacture for Vehicle Body，Hunan University，Changsha，410082

An envelope order spectrum based on multi－scale chirplet and sparse signal decomposition was proposed and applied to the fault diagnosis of gearboxes with rotating speed fluctuation.In the proposed method，the instantaneous frequency of gearbox meshing component was obtained by sparse signal decomposition based on multi－scale chirplet，and then the rotating speed signal can be got by software method without tachometer.After the vibration signals of a gearbox were analyzed by envelopment analysis，the even angle resampling on the envelope signals of the gearbox was carried out and the envelope order spectrum can be obtained，which can be used in the fault diagnosis of the gearbox.A simulation example and an example of its application have proved the effectiveness of the method.

sparse signal decomposition；envelope order spectrum；gear；fault diagnosis

TH113.1；TH165.3

1004—132X（2011）01—0069—06

2010—01—25

国家自然科学基金资助项目（50875078）；国家高技术研究发展计划（863计划）资助项目（2009AA04Z414）；湖南省工业科技支撑计划资助项目（2009GK2021）；高等学校博士学科点专项科研基金资助项目（20090161110006）

（编辑 郭 伟）

皮 维，男，1984年生。湖南大学机械与运载工程学院硕士研究生。主要研究方向为机械故障诊断技术。于德介，男，1957年生。湖南大学机械与运载工程学院教授、博士研究生导师。彭富强，男，1982年生。湖南大学机械与运载工程学院博士研究生。罗洁思，女，1985年生。湖南大学机械与运载工程学院博士研究生。