基于改进遗传算法的制造单元设计研究

范佳静 冯定忠

1.浙江工业大学，杭州，310014 2.浙江科技学院，杭州，310023

基于改进遗传算法的制造单元设计研究

范佳静1，2冯定忠1

1.浙江工业大学，杭州，310014 2.浙江科技学院，杭州，310023

针对制造单元构建问题的特征，构建了以总搬运成本以及机器设备的折旧和维修成本最低为主要目标，综合考虑了产品设备单元划分、单元内机器布局以及单元间布局的综合性制造单元模型。同时针对模型求解的复杂性，提出了改进遗传算法，并将其用于制造单元模型的求解。通过双层遗传算法，既保证了算法中染色体个体的有效性，又满足了遗传算法适者生存的根本原理；采用精英策略保证算法的收敛性；同时通过在求解过程中不断调整交叉算子和变异算子防止了算法收敛到局部最优解。最后将所提出的模型和改进的遗传算法应用于复杂实例，证明模型和算法的有效性。

制造单元；数学模型；改进遗传算法；精英策略

0 引言

单元制造是成组技术在企业中的具体应用，通过合理的单元构建、单元内机器布局以及单元间的布局，可以有效提高企业的生产效率、缩短准备时间和提前期，以及降低在制品成本等，从而降低企业的物料搬运成本、工具使用成本、设备成本以及员工聘用成本。因此近30年来国内外许多学者对其进行了大量的研究。

单元构建的方法有可视化编码、聚类分析、模糊聚类法、图论法、启发式算法、仿真模拟技术、数学规划法与智能技术等［1－8］。数学规划法应用智能技术解决单元构建问题，由于其目标函数及约束条件的任意选择性特点与实际生产过程中零件结构、批量以及工艺路径的多样性相符合，且便于应用计算机等先进手段的运用，因此这种方法在单元构建中最具应用潜力。

由于制造单元构建问题较复杂，虽然学者们已经提出了大量的规划模型，但是具有可实施性的制造单元应该是多种关联因素共同作用的结果，这些因素包括产品投产数量、加工的单位时间、加工工艺路径、设备能力、同种类型设备的数量（可选设备）等［9］，因此目前所考虑的数学规划模型中，还存在以下问题：①考虑同种设备只有一台，而实际情况是同种设备可能有2台或2台以上；②没有考虑零件操作存在多路径的问题，或者即使考虑到该问题，但是每条路径中的操作顺序没有明确；③同种设备的数量直接影响产品生产过程中的搬运次数和搬运成本，设备数量越多，则势必会减少物料的搬运次数，但是同样会增加设备的折旧和维修成本，然而在目前学者的研究中都没有同时考虑物料搬运成本与机器的折旧和维修成本这两个成本因素。

因此本文在假设单元布局为直线形而单元内机器布局为直线形或者L形的基础上，就以上三方面问题进行改进，提出一个一般性的单元制造0－1非线性整数规划模型，同时确定产品和机器的划分、机器布局以及单元布局使得总搬运成本与机器维修和折旧成本为最小。

1 模型分析

1.1 相关参数

p表示零件，p＝1，2，…，P；i，j表示机器，i，j＝1，2，…，M；r表示路径，r＝1，2，…，RP；op表示操作，op＝1，2，…，OP；k，k′表示单元，k，k′＝1，2，…，K；s，q表示单元内机器所处的位置；g，h表示单元所处的位置；Nmax为单元内允许拥有的最多机器数；Nmin为单元内允许拥有的最少机器数；Dintra为单元内相邻机器的移动距离；Dinter为相邻单元间的移动距离；Ni为第i种机器最多拥有的台数；Cintra为单元内的单位移动成本；Cinter为单元间的单位移动成本；Dp为第p种零件的年需求量；Bp为第p种零件的移动批量；Ci为第i种机器每年的维修和折旧成本；W 为一个无穷大的数。

Xipr（op）＝1表示第p种零件的第r条路径的第op 个操作需要使用机器i，否则 Xipr（op）＝0；Xik＝1表示第k个单元拥有机器i，否则Xik＝0；Xiks＝1表示第i种机器位于第k个单元的第s个位置，否则Xiks＝0；Xkg＝1表示第k个单元位于第g个位置，否则Xkg＝0；Xpr＝1表示第p种零件选择第r条路径进行操作，否则Xpr＝0；Xipr（op）k＝1表示第p种零件的第r条路径的第op个操作在单元k中的机器i上操作，否则Xipr（op）k＝0。

1.2 模型分析

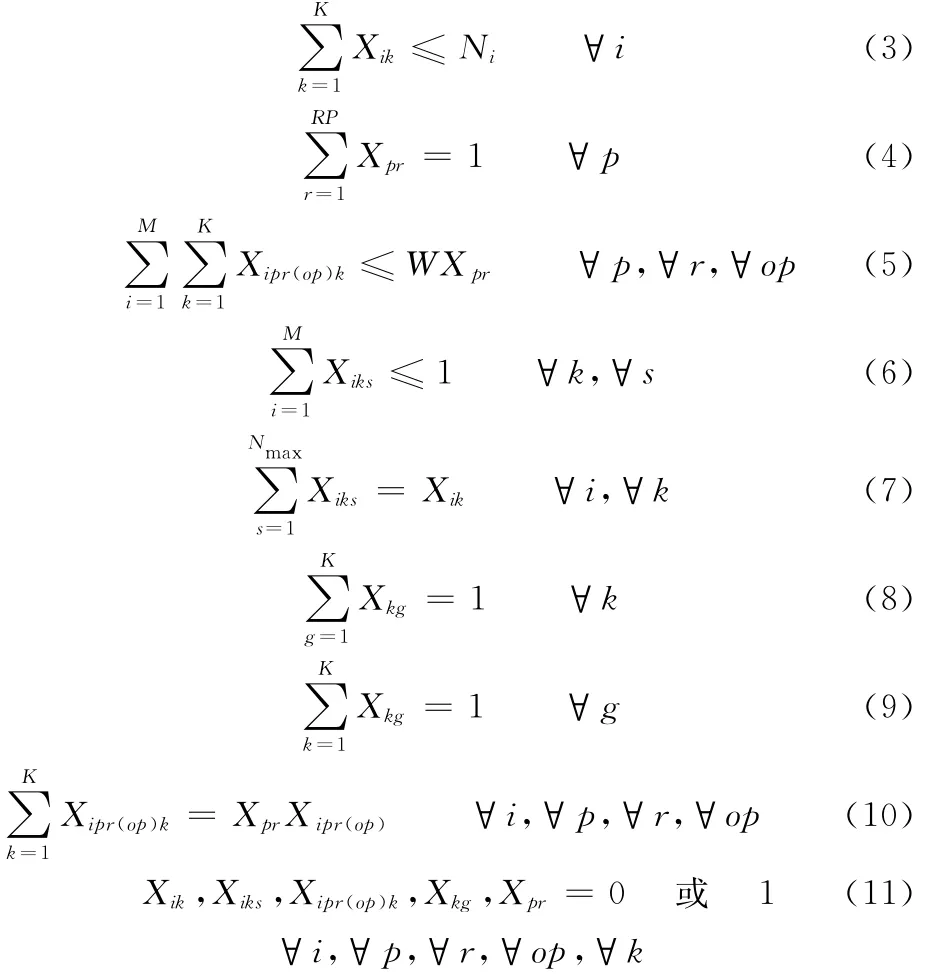
上述模型中目标函数表示综合考虑单元构建、机器布置和单元布置的情况下，使得总搬运成本和机器购买成本为最低。

约束条件中，式（1）和式（2）表示单元尺寸的限制；式（3）表示每种机器最多能够购买的数量；式（4）表示每种零件只能选择一条路径进行操作；式（5）表示如果某个零件的某条路径被选择，则该路径上的所有操作都必须进行；式（6）表示每个位置至多只能放置一台设备；式（7）表示每个设备只能放置于一个位置；式（8）表示每个单元只能固定于一个位置；式（9）表示每个位置只能设置一个单元；式（10）表示变量Xipr（op）k和变量Xpr以及变量Xipr（op）之间的关系；式（11）表示变量Xipr（op）k、Xik、Xpr、Xkg和Xiks均为0－1变量。

2 改进遗传算法

目前学者们已经提出了很多种制造单元构建问题模型的求解算法，如两阶段法、粒子优化算法、混合遗传算法、神经网络法、模糊算法等［9-16］。遗传算法是一种高效、并行、全局性的概率搜索算法。相比于传统的优化方法，遗传算法具有较好的全局搜索性能、不容易陷入局部最优等优势，适用于处理大规模的复杂非线性优化问题。但是针对不同的数学模型，由于变量和约束条件的特殊性，在运用基本遗传算法时往往会根据具体问题进行算法改进来适应模型的求解。针对上述提出的0－1非线性整数规划模型，鉴于其变量的复杂性以及较强的关联性，本文采用双层遗传算法、精英策略以及自适应算法来进行模型的求解，既加快了求解的速度，又有利于获得模型更好的满意解。

2.1 染色体编码

本文采取二进制编码和整数编码混合的方法进行变量染色体的设定。变量Xik和Xipr（op）k采取二进制编码，而Xiks、Xpr和Xkg则采取整数编码方式，如图1所示。通过这种编码方式可以使得随机选取的个体满足式（4）和式（6）～ 式（9）。

图1 染色体编码

2.2 双层遗传算法流程

由于变量Xik和Xpr与变量Xiks和Xipr（op）k之间存在较强的关联性，且对目标函数都有一定的贡献性，因此在运用遗传算法求解模型时，采用双层遗传算法来防止大量无效解的产生，从而加快运算速度。即首先确定变量Xik、Xpr和Xkg的初始种群，在对这三个变量运用遗传算法进行循环时，对与之相关的 Xiks、Xipr（op）k变量再套用遗传算法进行迭代优化，找出与每组Xik、Xpr和Xkg变量相对应的使得目标函数最优的 Xiks、Xipr（op）k。通过双层遗传算法既可体现遗传算法适者生存的本质，又可以保证所有的变量均满足式（5）和式（10）。具体过程如图2所示。

2.3 主层遗传算法

（1）选择策略。选择策略采用的是随机竞争选择方式。先通过普通方法计算选择概率，然后采用轮盘赌方法选出染色体对，通过染色体对之间的比较，使高适应度值的个体进入复制阶段。

（2）交叉算子。根据染色体结构，本文采用三点交叉方式进行交叉操作，在交配池中随机选取一对进行交叉的染色体后，再随机生成3个交叉点进行交叉，如图3所示。

（3）变异算子。对变量Xik和Xpr采用单点变异方式进行变异，变量Xkg则不进行变异。

（4）自适应算法。根据Srinvia提出的自适应遗传算法，交叉算子和遗传算子会随着个体适应度值自动改变。交叉概率Pc和变异概率Pm按照以下公式自适应调整：

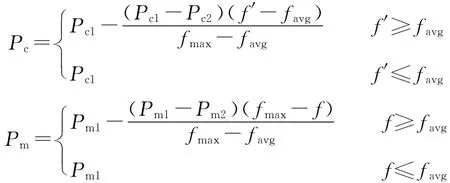
图2 双层遗传算法流程

图3 染色体交叉过程

其中，fmax为群体中最大适应度值；favg为每一代群体的平均适应度值；f′为待交叉的两个中较大适应度值；f为要变异个体的适应度值；Pc1＝0.9；Pc2＝0.6；Pm1＝0.1；Pm2＝0.01。

2.4 二层遗传算法

针对变量Xik和Xpr染色体个体的进化，通过二层遗传算法对与之有一定关联的Xiks和Xipr（op）k变量的染色体进行循环迭代，从而得到每一组Xik和Xpr的染色体相对应的Xiks和Xipr（op）k较优染色体。在第二层遗传算法中染色体的选择采用随机选择的方式任意选择一条染色体，然后根据相应的变异方式进行变异，其中不进行交叉过程。如图4所示，针对Xiks变量的染色体编码，每一单元分别选择两个不为零的随机点进行换位变异。而变量Xipr（op）k的染色体为0－1编码，因此迭代过程中采用单点变异的方法。

图4 Xiks染色体变异过程

2.5 精英策略

在每一次迭代完成时，为了提高群体进化水平，本算法还加入了精英策略方法。也就是每次迭代完成后的父代群体和子代群体合并，并按照适应度的高低进行排列，选择适应度高的Y1个群体作为下一次迭代的父代群体，以此保证每次迭代完成后的群体均为最优群体，并采用最优群体作为后代复制的基础。

2.6 迭代终止

对于主层次遗传算法，为了获得更好的适应度值，循环次数较多，一般T1取500～1000，而对于二层遗传算法，由于针对每一个变量Xik和Xpr染色体个体的改变都要进行一次迭代，同时在迭代的过程中容易出现重复的编码值，因此一次循环的次数可以相对较少，一般T2取20～50。

3 算例分析

本文应用上述模型和改进遗传算法对一个复杂算例进行建模，该问题共有18种机器和17种产品，每种产品有2条路径和3～6个操作，具体情况见表1。通过改进遗传算法对该问题进行求解，在第900代时收敛于最优解，到1000代时获得的最优解见表2，各零件选择的路径分别为2＿2＿1＿1＿1＿1＿2＿2＿2＿2＿1＿2＿2＿1＿2＿1＿2，设 备 6、10、15各有两台，而其他设备均为一台，同时存在4次单元间的移动，历代最优适应度值如图5所示。

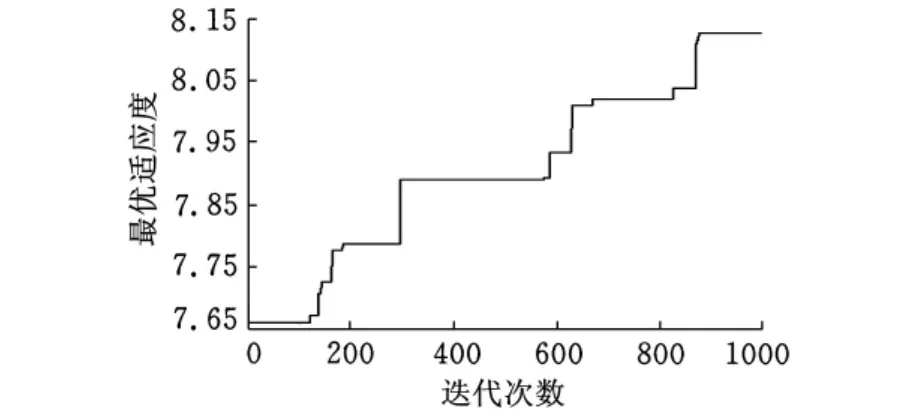
图5 历代适应度值

4 结束语

面对越来越激烈的市场竞争压力，以及客户对产品的多样化、个性化的需求和交付条件，许多企业已经或正在由传统的大批量生产方式向多品种、小批量的方式转变。在此背景下，各种先进的生产制造系统和生产制造方式被提出并应用于企业的生产实践。单元制造系统由于兼顾了大批量生产的成本和质量优势，以及多品种、小批量生产的快速响应能力，越来越受到企业的欢迎。

本文主要考虑到单元构建、单元内机器布局以及单元布局问题存在的相关性，在具有多路径和操作顺序，并允许扩大机器数量的基础上提出了制造单元模型，从而为企业合理安排机器零件加工提供了一定的数学依据。但是本文主要考虑的是单周期下需求已知的情况下的集成数学模型，而随着客户需求变化的不断扩大，对于不同产品的需求量也起伏不定，在不同时期产品的需求量是不恒定的。因此接下来的研究将进一步扩大到多周期环境中在需求不确定的情况下的单元制造问题。

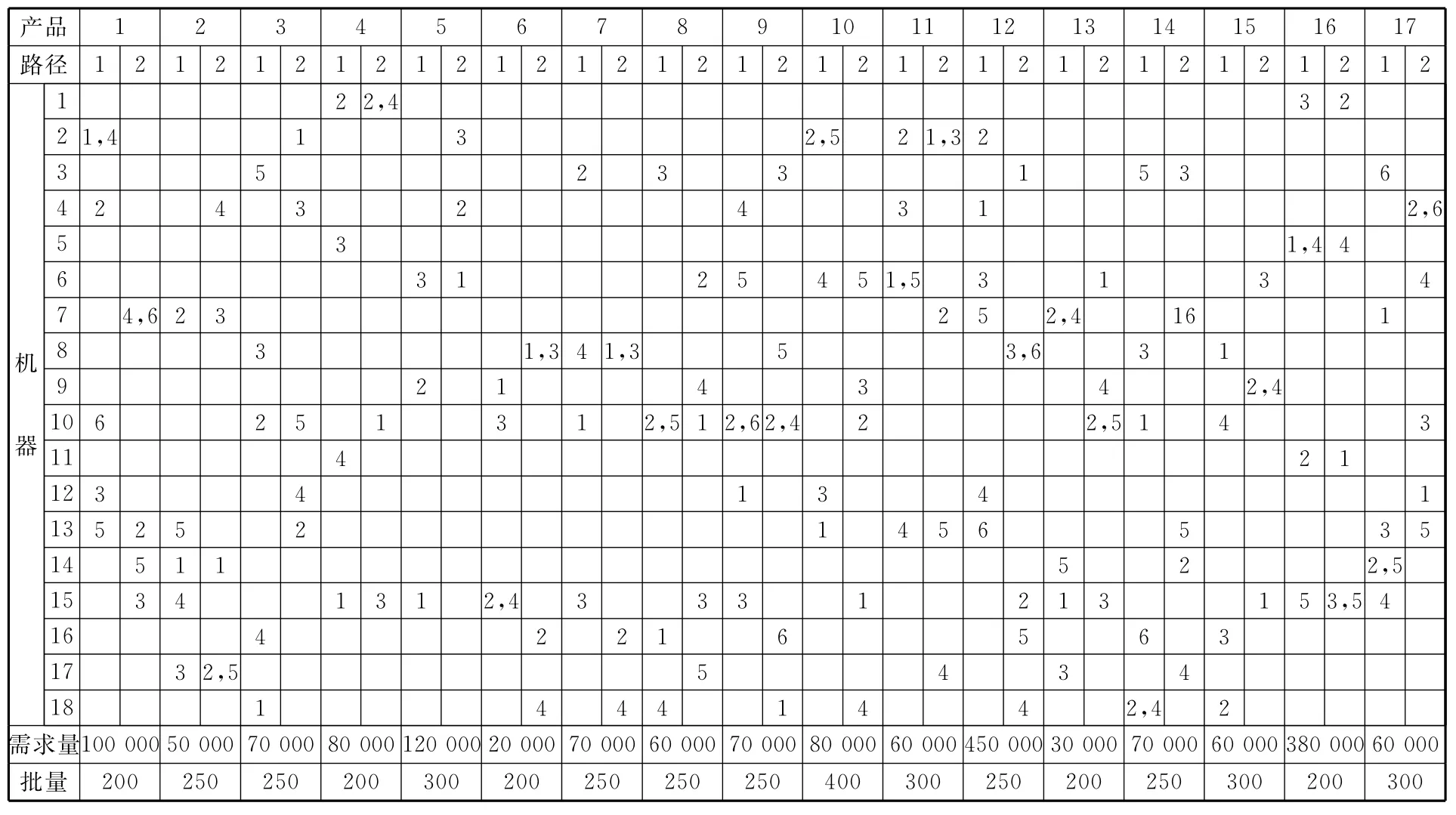
表1 机器与零件的关联表

表2 机器－零件单元划分、单元内机器分布以及单元分布表

［1］ Ahi A，Aryanezhad M B，Ashtiani B，et al.A Novel Approach to Determine Cll Formation，Intracellular Machine Layout and Cell Layout in CMS Problem Based on TOPSIS Method［J］.Computer ＆ Operation Research，2009，36：1478－1496.

［2］ Norman B A，Smith A E.A Continuous Approach to Considering Uncertainty in Facility Design［J］.Computers and Operations Research，2006，33：1760－1775.

［3］ Chiang C P，Lee S D.Joint Determination of Machine Cells and Linear Intercell Layout［J］.Computers ＆ Operations Research，2004，31：1603－1619.

［4］ Tavakkoli－Moghaddam R，Javadian N，Javadian B，et al.Desigh of a Facility Layout Probelem in Cellualr Manufacturing Systems with Stochastic Demands［J］.Applied Mathematics and Computation，2007，184：721－728.

［5］ 白书清，王爱民，李伯虎.面向应急动员批产的流水式制造单元构建技术［J］.计算机集成制造系统，2008，14（1）：64－73.

［6］ 刘敏，严隽薇，于轶.基于SOA的网格制造单元构造方法［J］.同济大学学报（自然科学版），2008，（10）：1417－1424.

［7］ 邵长运，初红艳，费仁元，等.基于专家系统的制造单元构建研究［J］.机械设计与制造，2008，（12）：100－103.

［8］ 王军强，孙树栋，王东成，等.基于约束理论的制造单元管理和控制研究［J］.计算机集成制造系统，2006，12（7）：1108－1121.

［9］ 王国新，阎艳，宁汝新，等.模糊神经网络与启发式算法相结合的制造单元构建方法［J］.计算机集成制造系统，2008，14（11）：2175－2185.

［10］ Chu C H.Genetic Algorithms for Integrating Cell Formation with Machine Layout and Scheduling［J］.Computer ＆Industrial Engineering，2007，53：277－289.

［11］ Chan Felix T S，Lau K W.Two－stage Approach for Machine－part Grouping and Cell Layout Problems［J］.Robotics and Computer－integrated Manufacturing，2006，22：217－238.

［12］ 康艳，朱宏，李旭伟.混合遗传算法在制造单元构建中的应用［J］.微计算机信息（测控自动化），2009，5（12）：186－188.

［13］ 李杰，王云峰，等.基于模糊技术的制造单元构建方法研究［J］.计算机集成制造系统，2004，10（12）：1561－1567.

［14］ 帅旗，陈耀军，杨莹.敏捷制造系统单元建模与优化研究现状综述［J］.机电工程，2008（5）：29－32.

［15］ 王东成，何卫平.神经网络在制造单元构建中的研究与应用［J］.中国机械工程，2006，17（5）：1040－1044.

［16］ 王雷，唐敦兵，等.基于粒子群优化算法的制造单元聚类研究［J］.计算机集成制造系统，2009，15（2）：328－332.

Study on Manufacturing Cellular Design Based on Advanced Genetic Algorithm

Fan Jiajing1，2Feng Dingzhong1
1.Zhejiang University of Technology，Hangzhou，310014
2.Zhejiang University of Science and Technology，Hangzhou，310023

A comprehensive model for manufacturing cellular was put forward which aimed at abtaining the minmum of material handling cost and machine depreciable and repair cost as well as synchronously considering the cellular formaiton，machine layout and cellular layout according to the characteristics of the problem of manufacturing cellular.And an advanced genetic algorithm was brought forward to solve this model.The individual validity and the characteristic of genetic algorithm were ensured；the convergence of algorithm through the elite strategy was ensured and the local convergence was protected by adjusting the crossover operator and mutation operator constantly.At last，the validity of the model and algorithm was proved by a complicated example.

manufacturing cellular；mathmatical model；advanced genetic algorithm；elite strategy

TH165

1004—132X（2011）01—0039—06

2010—03—09

浙江省自然科学基金资助项目（Y6090482，Y6090533）；浙江省钱江人才计划资助项目（2010R10096）

（编辑 郭 伟）

范佳静，女，1977年生。浙江工业大学机械工程学院博士研究生，浙江科技学院经济与管理学院讲师。主要研究方向为工业工程、可重构制造系统建模及控制、企业物流规划。冯定忠（通讯作者），男，1963年生。浙江工业大学机械工程学院教授、博士研究生导师。