水下重力异常相关极值匹配算法

李姗姗，吴晓平，马 彪

信息工程大学测绘学院，河南郑州450052

1 引 言

重力辅助导航是利用重力异常值或重力梯度值等辅助信息作为惯性导航系统的外部信息源，构成重力和惯性的组合导航系统［1－2］，从而起到抑制惯性导航误差的作用，具有自主性强、隐蔽性好、定位精度高、抗干扰性强等优点。

重力辅助导航的核心技术之一是重力图形匹配算法，其本质是综合利用各种信息处理方法，将实测海洋重力数据与存储在海洋重力数据库中的重力数据进行比较分析，依据一定准则判断两者之间的相似程度，从而确定出最佳匹配序列。采用的数据处理方法主要包括图像配准、相关极值分析、扩展卡尔曼滤波、神经网络和统计模式分析识别等［3－9］。针对重力匹配的特点，重点研究相关极值匹配算法中存在的问题及相应的改进措施，以期提高算法的可用性与可靠性。

2 重力序列相关极值匹配

根据文献［10］的相关极值导航系统原理，在进行重力异常相关匹配时，由于地球重力场的连续、随机、等值（多个地理点的重力异常值相等）特性，基于单个重力异常观测量无法唯一确定水下潜器在地图上的位置，因而要求其沿运动航迹方向的重力异常连续观测采样序列达到一定的长度。假定在时间序列ti，ti＋1，…，ti＋N－1时刻有N个重力异常观测向量，记为 Δgti＝［ΔgiΔgi＋1… Δgi＋N－1］T，根据每个时刻的惯导指示位置，在一定置信区间内，从事先存储在计算机内的重力基准图上搜索、提取若干与观测重力向量等长度的参考重力向量序列，记为最后两者之间通过某种相关极值匹配算法，来获取水下潜器当前位置的最优估计。常用相关分析匹配算法包括交叉相关算法（cross correlation，COR）、平均绝对差相关算法（mean absolute deviation，MAD）和平均平方差相关算法（mean square deviation，MSD）［9］，最优化匹配设计的准则是使COR取最大值，MSD、MAD取最小值，并以它们所对应的重力异常观测序列的航迹代替惯性导航指示航迹。

2.1 基于MSD准则的差分降权相关目标函数模型构造

观测序列与提取序列之间一般依据MSD相关算法，即目标函数为

基于上式寻找最优序列。式中，Δgi为对应于惯导输出点i的重力传感器的观测输出值，与置信区域内的重力异常图上的每个网格点的重力数据进行比较，如果为接近于0的判决阈值，依据重力图误差及重力传感器测量误差而定），则网格点j判定为惯导输出点i的重力等值点。由于惯导在较短的时间内的相对漂移很小，相邻连续两个实际点之间的位移角度及距离与相应惯性导航输出点位移角度和距离应该近似相等或相差很小。因此引入约束条件

式中，（xti，yti）、（xti＋1，yti＋1）是前后连续两个相邻时刻的坐标；ε1、ε2为接近于0的数值；αINS为惯导系统输出位移角度；dINS为惯导系统输出位移距离；Ω表示置信区间。

水下重力异常观测数据基于惯导输出的扰动修正［11］，由于厄特弗斯改正计算对水下潜器速度精度要求较高，正常重力计算要求纬度精度高，而惯导随时间积累产生的误差有可能满足不了这两项要求，观测重力异常的计算误差会随着惯导误差的增大而增大，以致产生重力匹配虚假定位。因而观测重力异常数据与重力异常图进行相关匹配时，还需考虑基于惯导输出计算厄特弗斯效应以及正常重力所产生的误差影响。

考虑到上述因素，在目标函数式（1）中基于差分思想，取前后连续两个时刻观测重力异常之差，形成一个新的观测序列，以尽最大可能减少这两项以及其他系统误差的影响。目标函数式（1）变为

式中，pi为相应的权系数。由于惯性导航误差随时间增加不断累积，因此相比较而言，前一时刻惯导输出数据应比后一时刻输出具有更高的精度与可信度，所以匹配过程中对前一时刻的观测量赋予比后一时刻更大的权值，定义该算法模型为差分降权相关目标函数模型。

通过试验计算发现，依据差分降权相关目标函数模型式（3）得到的对应于相关度量值最小的匹配序列结果有时并不是最好的。为解决这个问题通常采用所谓的“最近邻”方法，即简单认为离重力仪实际测量值序列最近的有效序列源于目标，其余有效序列均源于噪声干扰。但由于测量仪器（包括惯性导航元件、重力仪）误差、重力基准地图误差以及重力场相关性等因素的随机干扰，所有有效序列都可能源于目标，只是每个有效序列源于目标的概率有所不同，这种不确定性由概率密度函数表示。

2.2 概率数据关联匹配算法

在关于概率数据关联算法的研究中，文献［12］提出概率数据关联滤波器算法（probabilistic data association filter，PDAF）；随后文献［13］成功地将其应用于目标跟踪领域；文献［14］将其应用到地形辅助捷联式惯导中，并取得较好的效果；文献［15］也提出基于概率数据关联的地形辅助导航算法。笔者借用概率数据关联滤波的思想，提出基于概率数据关联的重力辅助惯性导航匹配算法，认为由于重力测量以及重力制图等各种噪声干扰，基于差分降权相关目标函数模型计算的最小相关度量值所确定的潜器位置并不一定完全代表水下潜器的真实位置，而可能小于某一阈值范围内的几个有效相关值确定的潜器位置都是不同概率意义上的实际地理位置，无形中提高了算法的可靠性。

2.2.1 概率数据关联滤波

令

表示重力传感器在k时刻确认的重力观测集合。gj（k）是k时刻的第j个重力观测；s（k）表示在k时刻确认的观测个数

为直到时刻k的所有重力测量集。假设θj（k）表示gj（k）是来自目标的正确测量事件；θ0（k）表示重力传感器所确认的观测没有一个是正确事件，则在k时刻第j个重力观测gj（k）是来自目标这一事件的概率密度函数为

由于｛θ0（k），θ1（k），…，θs（k）（k）｝是事件空间的一个不相交完备分割，从而有

因此利用全概率公式，可得

2.2.2 最优估值计算

取惯导位置偏移量［δφ δλ］T作为状态，小于某一阈值范围的相关度量值得到的匹配序列均认为是有效匹配序列，N为有效序列个数，根据式（8）得

2.2.3 概率密度函数计算

βj表示相关值p＿J（λj，φj）确定的位置为水下潜器实际位置的概率。相关值越小，所对应的位置是潜器实际位置的概率越高，且根据式（7）要求，取

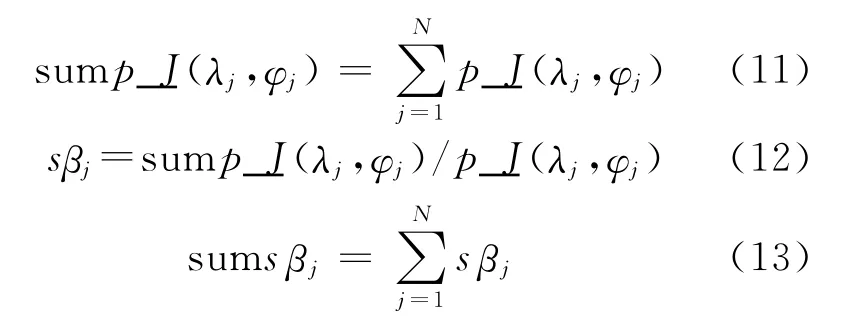
式中，p＿J（λj，φj）是依据差分降权目标函数模型式（3）计算的第j个重力异常图提取序列与重力异常观测序列的相关值的大小。

3 试验计算分析

3.1 数据仿真

采用航位推算法（dead reckoning，DR）推算航迹［16］，仿真条件：重力图分辨率为0.2′×0.2′，水下潜器航速为10kts，沿方位角52°方向航行，潜深是100m，惯导东向、北向、方位陀螺漂移均为0.01°／h，加速度计东向和北向零位漂移为5× 10－5g，东向、北向位置初始校准误差为1′，初始平台姿态校准误差为6″，重力仪的测量精度为0.5×10－5ms－2。某海域重力异常（卫星测高数据）变化试验区以及依据仿真条件模拟计算的惯导航迹与真实航迹如图1所示，图2是根据惯导误差传播特性计算的惯导位置误差仿真曲线示意图，图3反映仿真的惯导航迹与真实航迹上的重力异常变化。从图2可以看出由于惯导误差传播导致东向位置误差的无界性以及北向位置误差是地球周期占主项的振荡误差，如果不施于外部辅助手段对惯导进行校正，则随着时间推移惯性系统导航性能将失效。

图1 试验区惯导航迹与真实航迹仿真Fig.1 Simulation of the inertial navigation track and the real one in the experimental area

图2 惯导位置误差曲线示意图Fig.2 Sketch map of the position errors in inertial navigation

图3 惯导航迹与真实航迹上重力异常变化Fig.3 Variety of gravity anomaly on the inertial navigation track and the real one

3.2 重力匹配试验

在上述仿真条件的基础上，构造差分降权相关目标函数模型，将概率数据关联滤波算法应用于惯导航迹匹配校正，序列匹配长度取统计分析计算的试验区相关长度（6′左右），采样间隔取1个重力图格（仿真条件下约为90s），结果如图4。可以看出匹配结果并不是很理想，考虑到可能是由于采样间隔较短导致某些相邻采样点之间的重力数据相关性较强而出现虚假定位，于是加大采样间隔至2个重力图格（180s）、3个重力图格（270s）、4个重力图格（360s），分别进行匹配试验，结果如图5～图7所示，图中横坐标表示经度，纵坐标表示纬度。

图4 采样间隔90sFig.4 Sampling interval is 90s

对上述不同采样条件下的匹配结果进行统计分析，结果列于表1。可以看出，当采样间隔增大时，尤其从1个重力图格增加到2个或3个、4个重力图格时，精度均得到明显提高，但4个重力图格的采样间隔与3个重力图格的采样间隔相比较时，纬度精度改善不大，而经度方向误差甚至有所增大。分析原因，是因为当匹配序列长度保持不变时，增加数据采样间隔会减少采样点数，导致采样序列的采样点之间的相互约束条件减少而有可能使得匹配精度降低。

图5 采样间隔180sFig.5 Sampling interval is 180s

图6 采样间隔270sFig.6 Sampling interval is 270s

图7 采样间隔360sFig.7 Sampling interval is 360s

为进一步验证PDAF算法的可靠性，探讨采样间隔与匹配精度之间的关系，在上面仿真条件基础上，将惯导东向与北向初始位置误差均增加至5′，如图8、图9，采样间隔分别取1个重力图格、2个重力图格、3个重力图格、4个重力图格，进行重力匹配试验，结果如图10～图13所示，统计结果列于表2中。

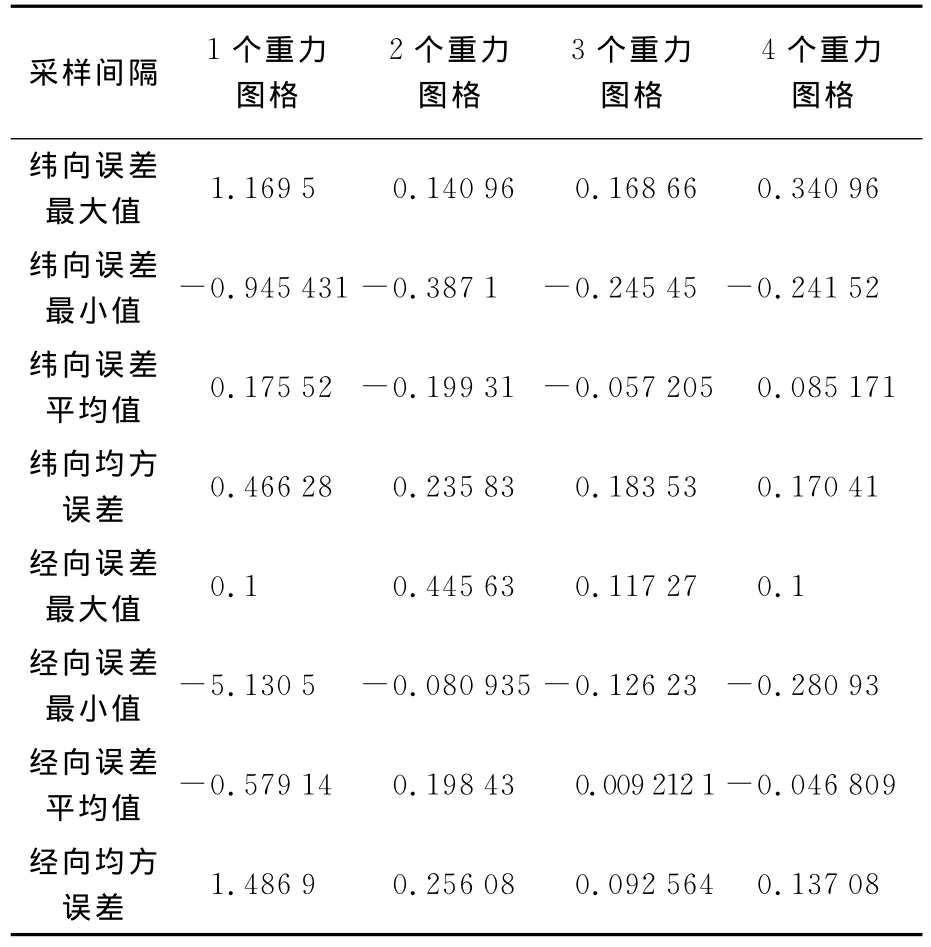
表1 不同采样间隔匹配算法位置误差统计Tab.1 Matching errors in position of various sampling intervals （′）

图8 试验区1的惯导航迹与真实航迹仿真Fig.8 Simulation of the inertial navigation track and the real one in the experimental area

图9 惯导航迹与真实航迹上重力异常变化Fig.9 Variety of gravity anomaly on the inertial navigation track and the real one

图10 采样间隔90sFig.10 Sampling interval is 90s

图11 采样间隔180sFig.11 Sampling interval is 180s

图12 采样间隔270sFig.12 Sampling interval is 270s

图13 采样间隔360sFig.13 Sampling interval is 360s

表2 不同采样间隔匹配算法误差统计Tab.2 Matching errors of various sampling intervals（′）

同前面分析的结论一样，当采样间隔从1个重力图格增加到2个或3个、4个重力图格时，精度均得到明显提高，但2、3、4个重力图格的采样间隔所获取的匹配序列精度，经度方向误差甚至有所增大。因此在选择采样间隔时，如果一味增加采样间隔，则会导致序列采样点数减少，从而使得采样点之间的相互约束条件减少而使得匹配的可靠性降低；而如果增大采样间隔的同时增加序列长度以保持前后采样约束条件数不变，虽然精度会有所提高，但这又是以增加惯导航迹匹配校正的时间为代价。所以在进行重力匹配时，需综合考虑这两方面影响，在重力特征明显的地区，序列长度与采样间隔可适当地取得短点，而在重力特征变化不是特别剧烈的地区，则应适当增加序列长度与采样间隔。综合惯导误差传播的特性（导致东向位置误差的无界性）以及表1和表2的匹配结果统计分析，对于该试验区的匹配，采样间隔选择270s为宜；同时也可以看出，采用本文建立的目标函数模型及PDAF匹配算法，即使惯导初始位置误差高达5′，也能将水平位置修正均方差控制在0.5′之内，充分说明了算法的可靠性。

4 结 论

为减少水下重力测量过程中的系统误差，基于差分的思想，提出以连续两个时刻观测重力异常之差作为新的观测匹配序列，并依据惯导误差累积特性，建立对前一时刻匹配量赋予更高可信度的差分降权相关极值目标函数模型，提出由于受干扰误差地影响导致源于正确位置出现多个有效位置的概率数据关联滤波算法，与选择“最近”的唯一位置相比更接近于实际的真实位置，增加算法的可靠性。探讨采样间隔对匹配精度的影响，提出进行重力匹配时要综合考虑序列长度与序列间隔两方面因素，以提高重力匹配导航的精度。

［1］ JIRCITANO A，DOSCH D.Gravity Aided Inertial Navigation System（GAINS）［C］∥Proceedings of ION 47th Annual Meeting.Washing DC：ION，1991：21－229.

［2］ YUAN Shuming，SUN Feng，LIU Guangjun，et al.Application of Gravity Map Matching Technology in Underwater Navigation［J］.Journal of Chinese Inertial Technology，2004，12（2）：13－17.（袁书明，孙枫，刘光军，等.重力图形匹配技术在水下导航中的应用［J］.中国惯性技术学报，2004，12（2）：13－17.）

［3］ XU Daxin.Using Gravity Anomaly Matching Techniques to Implement Submarine Navigation［J］.Chinese Journal of Geophysics，2005，48（4）：812－816.（许大欣.利用重力异常匹配技术实现潜艇导航［J］.地球物理学报，2005，48（4）：812－816.）

［4］ ZHANG Tonggang，CEN Minyi，FENG Yicong，et al.DEM Matching Algorithm Using Least Trimmed Squares Estimator［J］.Acta Geodaetica et Cartographia Sinica，2009，38（2）：144－151.（张同刚，岑敏仪，冯义从，等.采用截尾最小二乘估计的DEM匹配方法［J］.测绘学报，2009，38（2）：144－151.）

［5］ BEHZARD K P，BEHROOZ K P.Vehicle Location on Gravity Maps［C］∥Procee－dings of SPIE－The International Society for Optical Engineering.Orlando：SPIE，1999：182－191.

［6］ BEHZARD K P，BEHROOZ K P.Registration Algorithms for Geophysical Maps［C］∥Proceedings of MTS／IEEE Oceans’97Conference.Halifax：IEEE，1997：974－980.

［7］ WANG Kedong，CHEN Si.Iterative Closest Contour Point for Underwater Terrain－aided Navigation［J］.Joumal of Astronautie，2006，27（5）：995－999.（王可东，陈锶.水下地形匹配等值线算法研究［J］.宇航学报，2006，27（5）：995－999.）

［8］ BISHOP G C.Gravitational Field Maps and Navigational Errors［J］.IEEE Journal of Oceanic Engineering，2002，27（3）：726－737.

［9］ XIN Tinghui.The Research of Terrain－aided Underwater Navigation［D］.Xi’an：Northwest Polytechnical University，2004.（辛廷慧.水下地形辅助导航方法研究［D］.西安：西北工业大学，2004.）

［10］ KPACOACKUFI A A.The Theory of Correlative Extremum Navigation System［M］.REN Sicong translate.Beijing：Aviation Industry Press，1986.（克拉索夫斯基A A.相关极值导航系统理论［M］.任思聪，译.北京：航空工业出版社，1986.）

［11］ LI Shanshan，WU Xiaoping.Disturbance Correction of Gravity Sensor in GAINS［J］.Journal of Geomatics Science and Technology，2007，24（4）：270－273.（李姗姗，吴晓平.GAINS中重力传感器信息的扰动改正［J］.测绘科学技术学报，2007，24（4）：270－273.）

［12］ BAR S Y，TSE E.Tracking in a Cluttered Environment with Probabilistic Data Association［J］.Automatica，1975，11（5）：451－460.

［13］ BAR S Y，JAFFER A G.Adaptive Nonlinear Filtering for Tracking with Measurement of Uncertain［C］∥Proceedings of the 11th IEEE Conference on Decision and Control.Palo Alto：IEEE，1972：243－247.

［14］ DEZRET J.Improvement of Strapdown Inertial Navigation Using PDAF［J］.IEEE Transactions on Aerospace and Electronic System，1999，35（4）：835－856.

［15］ FENG Qingtang，SHEN Lincheng，CHANG Wensen.Terrain－aided Navigation Based on PDAF［J］.Joumal of Astronautie，2003，24（5）：439－443.（冯庆堂，沈林成，常文森.基于概率数据关联的地形辅助导航算法［J］.宇航学报，2003，24（5）：439－443.）

［16］ HUANG Motao，ZHAI Guojun，GUAN Zheng，et al.Surveying of Ocean Gravity Field and Applications［M］.Beijing：Surveying and Mapping Press，2005.（黄谟涛，翟国君，管铮，等.海洋重力场测定及其应用［M］.北京：测绘出版社，2005.）