一种基于高分辨率雷达影像以及外部DEM辅助的复杂地形制图方法

卢丽君，张继贤，王 腾

1.中国测绘科学研究院，北京100830；2.武汉大学测绘遥感信息工程国家重点实验室，湖北武汉430079

1 引 言

干涉合成孔径雷达（interferometric synthetic aperture radar，InSAR）作为一种主动的微波遥感技术在地形测绘已经显现出越来越大的优势［1－2］。针对国家一些重大的测绘生产任务，如西部测图任务，在坡度陡、高差大的西部地区进行高精度的DEM制图已经成为一项极具挑战性的任务。同时，由于TerraSAR－X、COSMO－SkyMed等高分率雷达遥感卫星的相继发射，这些具有强干涉能力的雷达传感器使高精度的DEM地形制图已经成为可能。

在应用InSAR技术生成DEM过程中，主要的误差源来自于相位误差［3－5］。相位误差主要由三部分组成：① 轨道误差引起的相位趋势误差；② 由于时间、空间去相关和热噪声造成的误差；③由于主从影像成像时间产生的大气差的扰动所引起的误差。为了更加精确地去除相位误差，外部DEM已经被应用到雷达干涉测量中，文献［6］提出了一种用粗的DEM方法减少干涉图的局部相位带宽，较低的相位带宽减少了相位残余，从而使相位解缠更加容易；文献［7］则有用外部的DEM减少高程的搜索范围；文献［8］使用SRTM通过构建线性模型最大程度地去除了相位误差。然而，针对坡度陡、高差大的复杂地形地区，单一的线性模型已无法拟合整个地形趋势，同时，在高分辨率雷达数据处理步骤中，如建立外部DEM模拟相位和干涉解缠相位的对应关系，在轨道参数精度低的条件限制下也严重影响最终的DEM精度。

本文针对坡度陡、高差大的复杂地形地区高精度DEM制图，首先根据雷达干涉影像的误差相位构建线性模型，在此基础上，研究一种外部DEM辅助下的DEM精化方法，最后应用于高分辨雷达影像（COSMO数据）在云南德钦地区的1∶50 000DEM制图。

2 相位误差分析

雷达影像干涉相位的表达式为

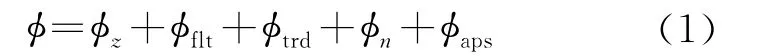
式中，φflt代表干涉相位中由于平地效应引起的相位；φz代表外部DEM产生的干涉相位；φn代表系统噪声引起的相位；φaps代表主从影像成像时间产生的大气差的残余相位；φtrd能够拟合由于轨道误差产生的相位误差和地形所产生的大气相位差的线性趋势，可以表示为［9］

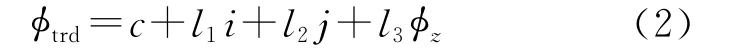
式中，c、l1、l2和l3代表线性趋势φtrd的线性系数。在把φflt和φz从干涉相位减去后，得到的相位差表示为

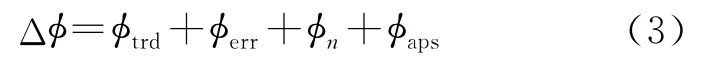
式中，φerr代表外部DEM引起的相位误差。这部分相位差将通过线性回归分析进行去除。在回归分析中，假设外部DEM引起的相位误差服从均值为零，标准方差为常量的标准正态分布。由于在回归分析有大量的样本点参与计算，φn和φaps的影响也基本可以忽略。因此，相位差的主要部分是φtrd。

除了以上建模的相位误差以外，在影像的某些像素上还存在解缠相位残余、雷达阴影等引起的相位粗差，这些粗差也直接影响最终DEM的产品精度。这部分粗差根据生成的DEM与外部DEM的距离范围进行滤波处理。

根据上述分析，外部DEM辅助下的DEM精化方法的核心是线性回归分析和系统粗差的滤除。

3 外部DEM辅助下的DEM精化方法

通过第二节对干涉相位的误差分析，外部DEM辅助下的DEM精化方法主要由建立外部DEM模拟相位和干涉解缠相位的对应关系，多模型的线性回归分析和高程点的滤波，如图1所示。

3.1 干涉图和外部DEM的精确对应关系建立

首先，通过应用轨道参数和高程值计算多普勒、距离和椭球方程来建立干涉图和外部DEM的初始的对应关系。然后，将真实的幅度和模拟幅度影像进行配准从而得到更加精确的对应关系。具体步骤为：

（1）初始地理编码表建立。应用轨道参数和高程值联合求解多普勒、距离和椭球方程将外部DEM从地理坐标的转化到雷达距离－多普勒坐标系下［10］，外部DEM的地理坐标和雷达坐标的初始对应关系被存储在地理编码表内。

（2）将雷达距离－多普勒坐标系下的外部DEM进行幅度影像模拟。

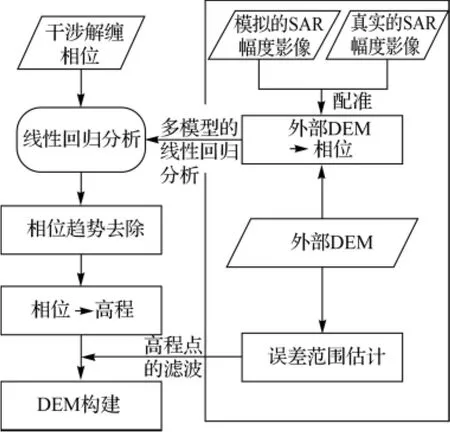
图1 外部DEM辅助下的DEM精化处理流程Fig.1 Working flow of DEM refinement facilitated by external DEM

Muhleman模型被用于描述雷达的后向散射系数σ［11］，对于不同的局部入射角η，有

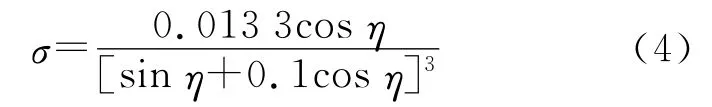
式中，K是常量，在雷达影像的某些区域，如叠掩和阴影区，Ps仅能反映后向散射的部分能量。

（3）真实的幅度影像和模拟幅度影像配准。多级配准技术将被应用于真实的幅度影像和模拟幅度影像配准。多级配准分为影像的粗配准和精配准。粗配准主要根据影像互相关函数的统计特性，通过在空间域内寻找两幅影像的互相关函数最大值进行配准，其精度可达到像素级。精配准对每一对粗配准的数据块在频率域内运用互相关函数进行配准，其精度可达到子像素级。一旦得到每个数据块的准确偏移量，双线性的配准多项式便可以确定。

（4）地理编码表的精化。真实的幅度影像和模拟幅度影像的精确对应关系确定下来后，便可用确定的二次多项式精化初始的地理编码表。利用精化后的地理编码表将外部DEM从地理坐标重新转化到雷达距离－多普勒坐标系下，外部DEM和干涉影像便建立了准确的一一对应关系。

3.2 多模型的线性回归分析

考虑到在高山地区地形的复杂性，在这种情况下多个回归模型将被采用。通过区域增长算法［12］把解缠后的干涉相位分割成几个子影像块，子块数目一般不宜过多（不超过10个），主要依据地形的变化进行分割。在每一个影像块上，按照下面的步骤进行回归分析。首先，把雷达距离－多普勒坐标系下的外部DEM按照式（6）转化成干涉相位，即

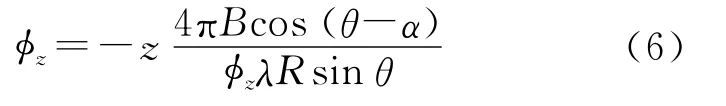
式中，φz是从外部DEM转化而来的干涉解缠相位；B是基线长度；R是斜距方向上目标到传感器的距离；θ是入射角；α是基线与水平方向的夹角；Z是外部DEM的高程值。

然后，选取相干性大于一定阈值（一般为0.5）的像素点作为可靠的点去拟合线性模型。对于分割的不同影像块，平均的相干性作为参考的阈值。一旦得到影像上每个像素的相位差Δφ，多个线性回归模型可写为

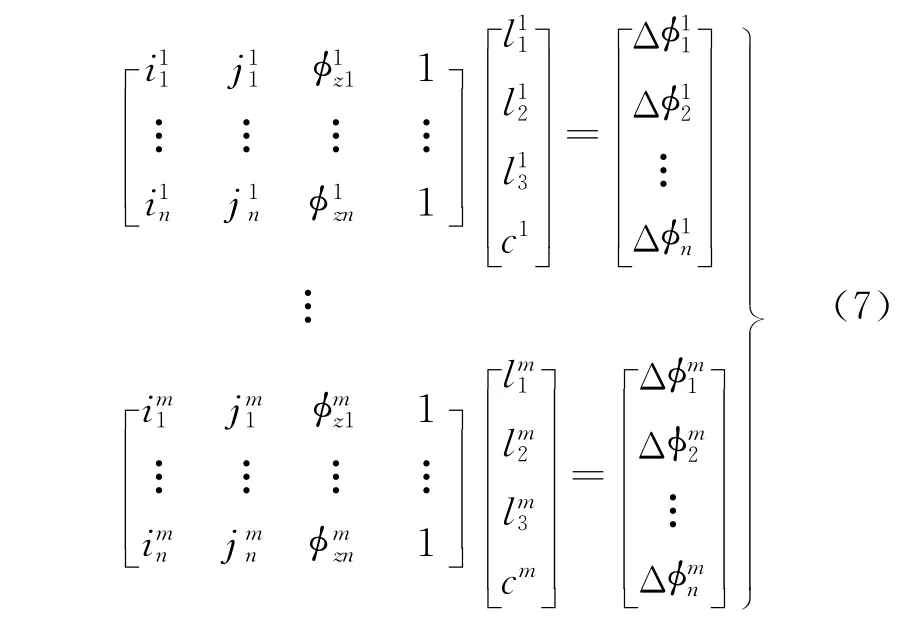
n和m分别代表每个模型像素点的个数和模型的个数，模型拟合系数m）能够由最小二乘拟合得到。为了正确地估计相位趋势，相位解缠中的残余相位将通过迭代过程逐步地被去除。即残余相位大于两倍标准差的像素点将被剔除，并且相位趋势迭代的被估计值到所有的像素点的残余相位都小于一定的阈值。应用多模型的线性回归，相位趋势能被逐像素地、准确地从干涉图中估计并去除。

3.3 不可靠的高程点的滤除

在去除了相位趋势以后，解缠干涉图能够转化成高程图，高程通过式（8）计算得到

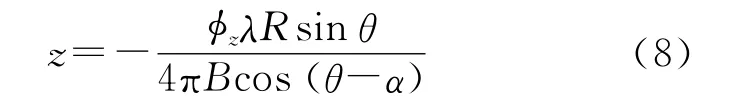
对于解缠干涉图的系统粗差的去除，主要依赖于InSAR得到的高程值与外部DEM的距离范围。基于Chebyshev理论，无论误差服从什么分布，任何误差在区间μ±4δ的概率至少是94%（μ和δ分别是误差的均值和标准偏差）。在该方法中，设置4倍的外部DEM误差作为去除不可靠高程点的标准。计算由InSAR和对应的外部DEM得到的高程点的绝对高程差，选择绝对高程差小于4倍的外部DEM误差的高程点并用于重构最终的DEM。

不可靠的高程点滤除后，由于InSAR影像在某些区域相干性较低，容易在影像中产生大的“空洞”（一系列连续的不可靠的高程点）。这里定义超过20个像素的连续区域定义为影像空洞，不可靠的高程点将被保留。而在较小的连续区域，其高程点将通过双线性插值方法得到。

4 试验与分析

4.1 试验区和数据介绍

以云南的德钦地区作为试验区，该地区的地形非常复杂：高差达到5 000m以上，平均坡度达到40°以上，同时该地区常年被冰雪覆盖。雷达干涉测量作为该地区的重要DEM测量手段和方法，选取相隔一天的3m分辨率COSMOSkyMed雷达干涉数据对，覆盖云南德钦地区约为1 300km2，具体数据参数见表1。

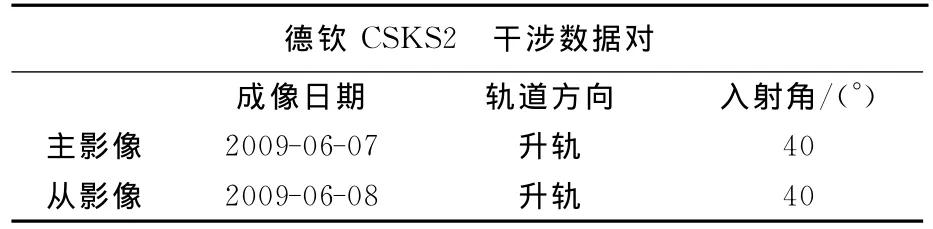
表1 数据集的基本信息Tab.1 Basic information of data sets

4.2 试验结果

在该试验中引入1∶100 000的外部DEM，应用轨道参数和高程值建立的初始地理编码表将外部DEM从地理坐标转化到雷达距离－多普勒坐标系下，同时进行SAR幅度影像模拟，如图2所示。从图2可以看出，经过影像模拟以后，模拟的SAR幅度影像和真实的SAR在细节上具有相似的纹理。

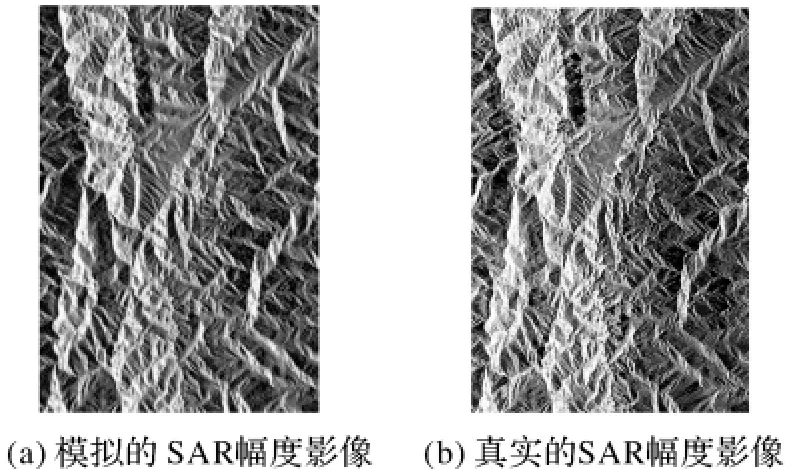
图2 模拟的SAR幅度影像和真实的SAR幅度影像比较Fig.2 Comparision of SAR simulated amplitude image and real amplitude image

利用模拟的SAR幅度影像和真实的SAR幅度影像的对应关系精化地理编码表，得到在几何关系上和干涉图一一对应的外部DEM，进而将外部DEM转化成解缠的干涉相位，如图3所示。最小费用流（MCF）算法用于干涉图的解缠［13］，得到的解缠后的干涉相位图，如图4所示。

图3 外部DEM的干涉相位图Fig.3 Phase with external DEM

图4 解缠后的干涉相位图Fig.4 Unwrapping phase

引入的1∶100 000外部DEM在高山地区的高程精度优于28m［14］，InSAR高程点的滤波阈值设置为4倍的外部DEM精度，约100m。将解缠后的干涉图根据区域增长算法分割成3个子影像块，如图5所示。在每个子数据块上选取相干性大于0.5的像素点进行线性回归分析，逐步地把相位趋势去除。在相位向高程转化过程中，InSAR生成的DEM和对应的外部DEM相减得到的绝对高程差大于100m的高程点将被滤除。理论上，有4 801 458个高程点（总共有16 444 755个高程点）将被滤除，但由于影像上存在“空洞”，实际上由4 695 825个点被滤除，其余的点保留InSAR生成的高程结果。最终的1∶50 000DEM的结果如图6所示，从局部的影像信息可以看出，精化后的DEM比未经过精化处理的DEM在细节信息上有了较大改进。

图5 解缠干涉相位分割结果Fig.5 Region segmentation result of phase

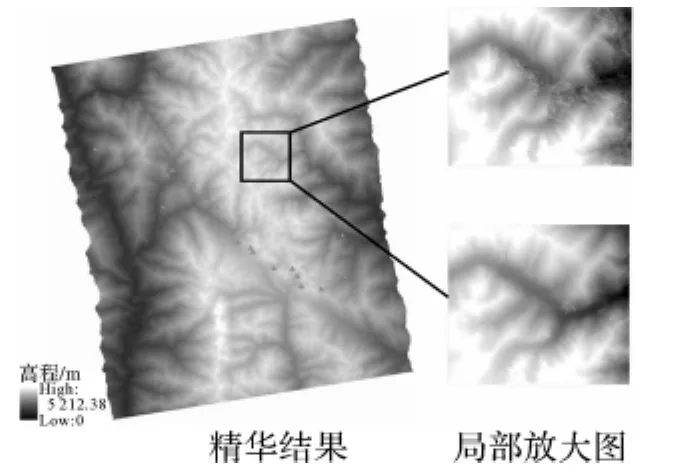
图6 1∶50 000 DEM结果 Fig.6 1∶50 000DEM result

4.3 结果验证

为了精确地验证所生成的1∶50 000DEM，23个验证点从GPS测量得到，分布如图6所示（三角形标记验证点），GPS点的测量精度达到毫米级。为了比较DEM精化方法和传统InSAR方法得到的DEM精度，在23个GPS检查点上进行高程的误差比较。如图7所示，由DEM精化方法得到高程精度比传统的InSAR方法有了一定程度的改善，同时高程误差的分布也更加均匀。通过在这些检查点上计算得到，传统InSAR方法得到的DEM的标准偏差为40.9m，DEM精化方法得到的DEM的标准偏差为19.7m。

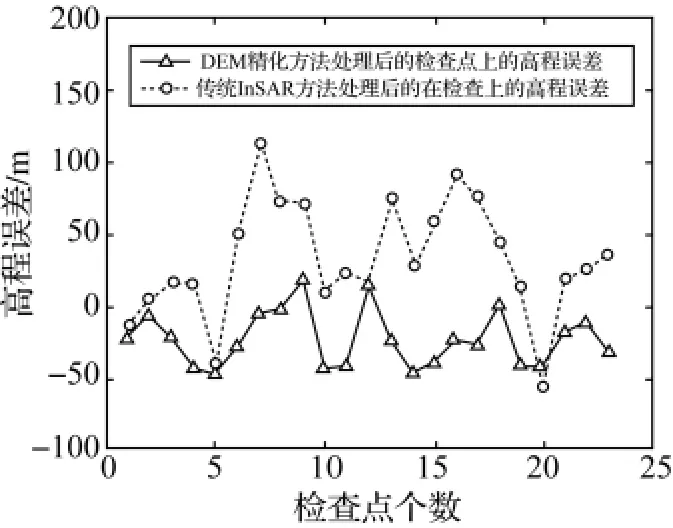
图7 在GPS检查点上的高程误差分布Fig.7 Height errors distribution on check points

4.4 计算效率分析

为了分析该方法的计算效率，将SAR影像分成不同面积大小的数据块，使用配置为双核2.66GHz的CPU，内存2G的计算机进行处理。如图8所示，DEM精化方法的处理时间是随着SAR影像的处理面积而增大的，处理一整景SAR影像的时间约为8 000s。在DEM精化处理中，多模型的线性回归分析所占的时间最长，约为整个处理时间的三分之二，它主要取决于选取参与回归计算的像素点数目。

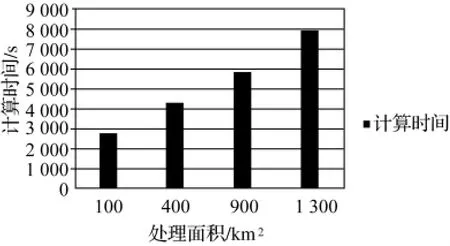
图8 DEM精化方法的处理时间Fig.8 Processing time of DEM refinement

5 结 论

针对在地形复杂区域的高精度雷达制图的需要，发展了一种基于高分率雷达影像的外部DEM辅助下的复杂地形制图方法。本方法的特点之一是实现了外部DEM和干涉图精确的一一对应关系，另一特点则是运用多模型的线性回归策略拟合了地形趋势并去除了相位误差，也利用了引入的外部DEM很好地去除了系统粗差。通过精度的比较和分析，本方法得到的DEM精度比传统的InSAR方法有了一定程度的提高，其高程精度（19.7m）能满足国家1∶50 000DEM地形制图要求［14］，但计算效率有待提高，今后可采用多任务并行的计算方式改善其计算效率。云南德钦地区作为复杂地形的代表试验区，其试验结果证实了该方法在复杂地形区域应用高分辨雷达影像的制图能力。同时，该方法也已经推广至国家西部测图项目的生产任务中，适用于平地、丘陵和高山等各种地形区域，在应用星载TerraSAR、Radarsat－2和COSMO－SkyMed等高分辨干涉SAR影像进行DEM制图上已经取得了较好的效果。

［1］ GUO Huadong.Theories and Application of Radar for Earth Observation［M］.Beijing：Science Press，2000：131－135.（郭华东.雷达对地观测理论与应用［M］.北京：科学出版社，2000：131－135.）

［2］ ZHOU Jianmin，LI Zhen，LI Xinwu.Research on Rules of the Valley Glacier Motion in Western China Based on ALOS／PALSAR Interferometry［J］.Acta Geodaetica et Cartographica Sinica，2009，38（4）：341－347.（周建民，李震，李新武.基于ALOS／PALSAR雷达干涉数据的中国西部山谷冰川冰流运动规律研究［J］.测绘学报，2009，38（4）：341－347.）

［3］ ZEBKER H A，VILLASENOR J.Decorrelation in Interferometric Radar Echoes［J］.IEEE Transactions on Geoscience and Remote Sensing，1992，30（5）：950－959.

［4］ ZEBKER H A，WERNER C L，ROSEN P A，et al.Accuracy of Topographic Maps Derived from ERS－1Interferometric Radar［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32（4）：823－836.

［5］ ROSEN P A，HENSLEY S，JOUGHIN I R，et al.Synthetic Aperture Radar Interferometry［EB／OL］.［2010－01－12］.http：∥www.gps.caltech.edu／classes／ge167／file／Rosen＿IEEE2000＿Insar.pdf.

［6］ SEYMOUR M S，CUMMING I G.InSAR Terrain Height Estimation Using Low－quality Sparse DEM’s［C／OL］∥Proceedings of the 3rd ESA Scientific Symposium on ERS Satellites，Florence：［s.n.］，1997［2010－01－12］.http：∥florence97.ers－symposium.org／.

［7］ EINEDER M，ADAM N.A Maximum－likelihood Estimator to Simultaneously Unwrap，Geocode，and Fuse SAR Interferograms from Different Viewing Geometries into One Digital Elevation Model［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43（1）：24－36.

［8］ LIAO Mingsheng，WANG Teng，LU Lijun，et al.Reconstruction of DEMs from ERS－1／2Tandem Data in Mountainous Area Facilitated by SRTM Data［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（7）：2325－2335.

［9］ HANSSEN R F.Radar Interferometry：Data Interpretation and Error Analysis［M］.Dordrecht：Kluwer Academic Publishers，2001.

［10］ GEUDTNER D.The Interferometric Processing of ERS－1 SAR Data［R］.［S.l.］：European Space Agency.2006.

［11］ MUHLEMAN D O.Radar Scattering from Venus and the Moon［J］.The Astronomical Journal，1964，69：34－41.

［12］ ADAMS R，BISCHOF L.Seeded Region Growing［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1994，16（6）：641－647.

［13］ COSTANTIN M.A Novel Phase Unwrapping Method Based on Network Programming［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36（3）：813－821.

［14］ State Bureau of Surveying and Mapping.CH＼T1008－2001 Digital Products of Fundamental Geographic Information 1∶10 000，1∶50 000Digital Elevation Models［S］.Beijing：Surveying and Mapping Press，2001.（国家测绘局.CH＼T1008－2001基础地理信息数字产品1∶10 000、1∶50 000数字高程模型［S］.北京：测绘出版社，2001.）