n-精化与n-互模拟之间相关问题的研究

施晓静，张晋津

(1.南京航空航天大学 计算机科学与技术学院,江苏 南京 210016；2.南京审计学院 计算机科学与技术系,江苏 南京 211815)

0 引 言

由于分布式计算技术的进步，将分布式技术与人工智能相结合，从而得到的分布式人工智能正逐渐受到研究专家和学者的重视。分布式人工智能的研究主要集中在多agent之间的合作、交互等方面[1]。因此，在大多数情况下，一个agent就需要同其他agent联合起来去解决一个问题，在这种情形下，各个agent间进行信息传递与信息更新是不可避免的。如何形式化地刻画agent的认知所遵循的逻辑规律成为学者们最关心的问题之一。

Hans vanDitmarsch等引入了未来事件逻辑(future event logic,FEL)[1]，通过在模态逻辑中添加新算子∀φ和对偶的∃φ刻画对多agent系统的认知，其中，∀φ表示在任意信息事件[2]之后，φ都会成立。随后，Hans van Ditmarsch等将精化模态逻辑(refinement modal logic,RML)看作是FEL的抽象[3]，因此∃算子表示对精化的量化，也称为精化量词，用以描述与所给的信息状态相匹配的信息事件。

随着研究的不断深入，学者们逐渐意识到，在不同的模态逻辑下用结构转换来解释精化量词具有更广泛的意义，由此，Laura Bozzelli等在Hans van Ditmarsch研究的基础上，进一步将精化量词引入模态逻辑，并展开了相关的研究工作。精化与互模拟的区别在于前者只需满足(back)条件,而对(forth)条件并没有限制[4-5]。

文中将对精化关系加以层次的限制，进一步探究n-精化关系(n-refinement)。基于Laura Bozzelli等的研究工作[6]，将着眼于n-精化与n-互模拟之间的转换关系，提出相对化的概念，从而建立基于语义等价的从n-精化模态逻辑到n-互模拟量化逻辑的翻译函数。

1 预备知识

令A表示有限的agent集合，P表示可数的命题变元集合，表示自然数集。用a,b,a',b',…表示A中的元素，并且用p,q,r,p',p'',…表示P中的元素。

下面参考n-互模拟[7]引入n-精化关系的概念。

定义1(n-精化，n-互模拟)：对任意B⊆A及模型M=(S,R,V)和M'=(S',R',V')，二元关系序列{Zi}i≤n是M和M'之间关于B的n-精化关系(n-refinement)，当且仅当Zn⊆…⊆Z0⊆S×S'且对任意(v,v')∈S×S'，a∈A-B，b∈A以及0≤i≤n，如下条件成立：

(atoms)如果vZ0v'，那么对于任意p∈P，v∈V(p)当且仅当v'∈V'(p)；

对于任一给定n∈及B⊆A，点模型上的二元关系定义如下：当且仅当M与M'之间存在关于B的n-精化关系{Zi}i≤n使得sZnt。亦采用记号说明{Zi}i≤n是M与M'之间存在关于B的n-精化关系且sZnt。当B={a}时，将表示为不难得证，对于任意n∈，本身是一个n-精化关系。

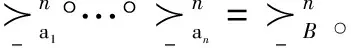
本节将给出n-精化模态逻辑的语法、语义及其可靠完备的公理系统。

2.1 语言及语义

定义2(n-精化模态逻辑语言L∀n)：令A是一个有限agent集合，P是原子命题的可数集合，L∀n公式由以下BNF范式定义，其中B⊆A，a∈A，p∈P且n∈。

φ::=p|

定义3(n-精化模态逻辑的语义)：公式L∀n的可满足性归纳定义如下：

Ms|=p当且仅当s∈VM(p)；

Ms|=φ当且仅当Ms|≠φ；

Ms|=φ∧ψ当且仅当Ms|=φ且Ms|=ψ；

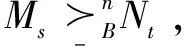
定义4(n-互模拟量化逻辑语言L∀n)：L∀n公式可按以下BNF范式归纳定义：

φ::=p|

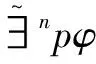
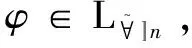
由命题1可知如下结论成立：

2.2 n-精化的语义操作

根据定义2可知，n-互模拟是n-精化关系，反之却不成立。这一节研讨n-互模拟关系和n-精化关系之间的联系。

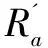
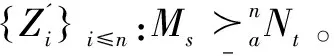
(1)S'≜SM∪SN；

(2)对任意b∈A:

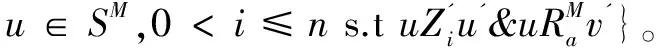
(3)V'≜VM∪VN。

证明：类似引理1，令R''=RN，原子命题p在N'中SM域上为假，SN域上为真即可得证。

3 语言L∀n到的翻译

首先引入相对化的定义。

q(a,p)=q；

(φ∧ψ)(a,p)=φ(a,p)∧ψ(a,p)；

(□aφ)(a,p)=□a(p→φ(a,p))；

(□bφ)(a,p)=□b(p→φ(a,p))，其中b≠a；

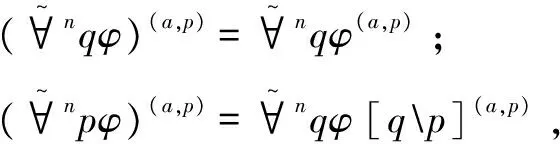
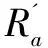
证明：根据公式φ的结构复杂度归纳证明。

对不同的原子命题关于不同agent进行相对化与顺序无关，下面给出具体验证过程。

证明：根据公式φ的结构复杂度不难得证。

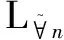
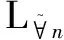
t(p)=p；

t(φ)=t(φ)；

t(φ∧ψ)=t(φ)∧t(ψ)；

t(□aφ)=□at(φ)；

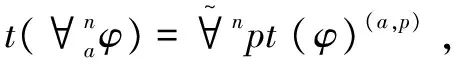
下面给出含多个不同n-精化算子的L∀n公式的翻译。

例1：

命题4：给定点模型Ms，对于任意φ∈，均有Ms|=φ当且仅当Ms|=t(φ)。

证明：按照φ∈L∀n的结构复杂度证明。

4 结束语

目前，关于精化模态逻辑已经有比较完善的研究结果，Hans等已经给出了从精化关系到互模拟关系的转换过程，由此RML语言翻译成互模拟量化逻辑语言[11-12]，并将该结果应用于RMLμ公理系统的可靠性证明中[12-13]。文中提出了n-精化关系的概念，基于n-互模拟和精化的定义[14]，给出n-精化的定义及其数学性质。在n-精化的语义操作前提下，研究n-互模拟、n-精化关系之间的关系，因此提出了相对化[15]的概念，比较了相对化概念与标准相对化之间的区别与联系。在此基础上考察将n-精化模态逻辑语言翻译成n-互模拟量化逻辑语言。未来的研究工作会将n-精化模态μ演算翻译成n-互模拟量化语言，并探究n-模态μ演算公理系统[16]的可靠性与完备性。

参考文献：

[1] VAN DITMARSCH H,FRENCH T,PINCHINAT S.Future event logic-axioms and complexity[C]//Seventh conference on advances in modal logic.[s.l.]:[s.n.],2010:77-99.

[2] VAN DITMARSCH H,FRENCH T.Simulation and information:quantifying over epistemic events[M]//Knowledge representation for agents and multi-agent systems.Berlin:Springer-Verlag,2009:51-65.

[4] BLACKBURN P, DE RIJKE M, VENEMA Y. Modal logic[M]//Cambridge tracts in theoretical computer science.Cambridge:Cambridge University Press,2001.

[5] D’AGOSTINO G,LENZI G.An axiomatization of bisimulation quantifiers via the μ-calculus[J].Theoretical Computer Science,2005,338(1-3):64-95.

[6] BOZZELLI L,VAN DITMARSCH H,FRENCH T,et al.Refinement modal logic[J].Information and Computation,2014,239:303-339.

[7] KUPKE C,KURZ A,VENEMA Y.Completeness of the finitary Moss logic[C]//Seventh conference on advances in modal logic.[s.l.]:[s.n.],2008:193-217.

[8] VENEMA Y.Lectures on the modal μ-calculus[D].Beijing:Renmin University in Beijing,2008.

[9] FRENCH T N.Bisimulation quantifiers for modal logics[D].Australia:University of Western Australia,2006.

[10] D’AGOSTINO G,HOLLENBERG M.Logical questions concerning the μ-calculus:interpolation,Lyndon andos-Tarski[J].Journal of Symbolic Logic,2000,65(1):310-332.

[11] CHISWELL I,HODGES W.Mathematical logic[M].[s.l.]:[s.n.],2007.

[12] HALES J.Refinement quantifiers for logics of belief and knowledge[D].Australia:University of Western Australia,2011.

[13] HALES J,FRENCH T,DAVIES R.Refinement quantified logics of knowledge[J].Electronic Notes in Theoretical Computer Science,2011,278:85-98.

[14] HALES J,FRENCH T,DAVIES R.Refinement quantified logics of knowledge and belief for multiple agents[C]//Seventh conference on advances in modal logic.[s.l.]:[s.n.],2012:317-338.

[15] 钮 俊,曾国荪,王 伟.绿色评价模型的互模拟等价及逻辑保持[J].计算机学报,2013,36(5):967-976.

[16] 颜 锋,田作威,严榴香.多态π演算的互模拟等价关系及其公理化[J].计算机工程与科学,2010,32(10):131-134.