一种基于SOM划分的FP-growth算法

郏奎奎，刘海滨

(中国航天系统科学与工程研究院，北京 100048)

0 引 言

数据挖掘被称为数据集中的知识发现，是在大量数据集中提取对于决策过程有用的知识的过程。数据挖掘自20世纪90年代被提出后，在许多领域得到了很好的应用。关联规则挖掘是数据挖掘的重要组成部分。1993年，R.Agrawal等[1]提出了关联规则的概念及模型，该模型主要是对一个事物和其他事物相互关联的一种描述。目前，主要的关联规则挖掘算法有Apriori和FP-growth，二者都是串行化的算法。Apriori[2]算法需要多次扫描数据集，过程中产生了大量候选集，测试这些候选集需消耗大量时间。FP-growth算法是一种基于频繁模式树的挖掘算法。该算法可以有效挖掘频繁模式，并且比Apriori算法快大约一个数量级。但是随着数据量的增大和数据集中的有用信息变得越来越稀疏，在建立FP-tree时会消耗大量的内存空间，以至于内存不够用，无法完成挖掘任务[3-4]。Park等[5]提出利用系统抽样的方法进行数据挖掘，然而单纯只依靠抽样的数据进行数据挖掘很容易造成结果的畸形和不准确。因此，学者们开始考虑通过并行计算环境来解决上述问题。文献[6]采用基于多线程的并行算法，虽然缓解了存储及计算的压力，但是内存资源的局限制约了算法的扩展能力；文献[7-8]中对MPI并行环境进行了详细的叙述，然而该环境使用进程间通信的方式协调并行计算，导致并行效率较低、内存开销大并且很难解决多节点的扩展性问题。并行算法通常具有较大的进程间的调度和通信开销，并且很难将构建FP-tree的任务进行分割。

在前人研究成果的基础上，文中提出了一种改进的FP-growth算法。众所周知，数据集中高频率的项集是包含在每条事务中的，那么含有频繁项集的事务之间的欧氏距离总是较小的，所以数据集中的事务会具有聚类现象。利用SOM等聚类算法对其做聚类分析，再在每个类别上并行执行数据挖掘算法就可以得到挖掘结果了。首先利用聚类算法对数据集进行分割，然后在每个数据子集上并行执行FP-growth算法，这样就将算法所需要的大内存空间分割成小内存进行运算了，并且由于子集是根据聚类结果划分的，所以在各个子集上能够高效地挖掘出有用的关联规则，而非由于随机划分数据集导致挖掘出具有不确定性的规则。由于数据量较大，对大数据集做聚类分析会耗费大量的计算资源，所以文中利用系统抽样方法从大数据集中抽取出具有代表性的样本，然后利用SOM算法对样本进行聚类分析，得到分类模型，利用该模型将整个数据集分成若干个子集，并在各个子集上采用FP-growth算法挖掘出关联规则，最后将关联规则合并得到总的结果，并通过实验验证了该算法的有效性。

1 SOM算法相关研究

聚类分析是目前数据挖掘的研究热点之一，聚类分析能够将数据聚类成为多个类或簇，从而使得在同一个类中的数据具有比较高的相似度，而不同类的数据之间有比较大的差别[9]。聚类分析过程是无监督的分析过程，在对数据进行分类之前，对类别数据是未知的。经典的聚类分析算法有K-means、CURE等，这些算法需要提前设定聚类的类别数。这种事前设定类别数的做法大多基于程序设计经验，并且需要经过不断试验才能得到比较正确的分类，这种做法具有一定的不确定性，在一定程度上降低了聚类分析结果的可信度。自组织映射(self-organizing map)是由芬兰学者Kohonen提出的一种只有两层神经网络的算法。SOM的权值调整方法与其他神经网络相似，都是采用梯度下降法不断地调整权值。它比较特有的地方就是将高维数据点按照原有的顺序拓扑关联到二维平面网格节点上，这样就实现了高维数据的二维结构可视化。此外，由于SOM的高维数据的低维表达能力，SOM在数据分类、聚类等应用领域有很多成功的应用案例。文中利用SOM聚类算法实现对海量数据的聚类分析，进而利用聚类模型对数据库进行分割，并在各个子集上进行FP-growth数据挖掘。

1.1 SOM算法描述

SOM神经网络算法是一种特殊的神经网络，由输入层和输出层构成。在输入层上只存在一个神经元节点，该神经元节点对应于输入向量x=[x1,x2,…,xd]，其中d是输入数据维数；在输出层上有一系列的组织在二维平面网格上的神经元节点。每个神经元节点都相应地有一个权矢量m=[m1,m2,…,md]。SOM神经网络权值的训练步骤如下：

(1)设定输出层每个节点的初始权重值。通过预先定义一个训练长度或者设定程序终止的误差阈值，来判断训练的终止条件。

(2)在数据集中选取一个样本x，计算样本与每个输出层神经元节点之间的欧氏距离,然后选取与样本x距离最近的神经元节点,该神经元节点称为该样本的最佳匹配节点(best-match unit,BMU),记为mc。

‖x-mc‖=min{‖x-mi‖}

(1)

(3)依据预先设定的邻域函数来确定BMU邻域的范围,进而利用调节函数调整BMU及其邻域内神经元节点的权重值:

mi(t+1)=mi(t)+a(t)hci(t)[x(t)-mi(t)]

(2)

其中，mi(t)为第t步节点i的权值；a(t)为第t步的学习率；hci(t)为邻域函数。

学习率一般伴随着训练的推进而逐渐变小,这里一般选择按线性减小、指数减小的方式。这里的邻域函数通常使用高斯函数或者气泡函数。

(4)如果还没有达到训练结束的条件,则返回步骤(2)继续训练。

1.2 聚簇分布特征图

人们通常难以从高维数据中区分出数据的分布特征，然而SOM算法能够将高维数据拓扑保序地映射到二维平面网格上，映射后的数据结构具有显著的聚类特征，从而能够高效地识别出聚类数据。文中利用SOM算法的这一特征来实现大数据集的聚类分析。众所周知，很多算法在进行聚类分析之前往往需要盲目地确定聚类的簇数，尤其随着数据的增大，这种方法往往效果很差。针对这种情况,设计了一种聚类分布特征图,这个特征用来在聚类前先对数据进行预处理,这样就能快速获得数据分布的特点,从而确定数据聚类的类别数目。

通常训练好的SOM神经网络的输出层往往组织成一个网络结构,然后对每个神经元节点按列优先进行编号。假定SOM输出层共有m*n个神经元节点，则定义下面的距离矩阵(distance-matrix)，简称D-matrix：

(3)

其中，dij表示第i个神经元节点与第j个神经元节点之间的欧氏距离。

接着将距离与一个颜色范围建立一一对应的关系，一般在灰度模式下，距离自小到大，距离所对应的颜色由浅至深，所以就可以得到一个与距离矩阵相对应的颜色矩阵(color-matrix)，简称C-matrix。

(4)

其中，cij表示与dij相对应的颜色取值。

对每个输出层节点根据颜色矩阵进行灰度值的着色，那么就得到了一张聚类分布特征图，根据聚类分布特征图就可以确定聚类个数。

2 FP-growth算法研究

2.1 关联规则挖掘的定义

关联规则是对一个事物和其他事物相互关联的一种描述。关联规则的挖掘就是从大量的数据集中找出这些数据之间的相互联系。衡量规则的2个度量是支持度和置信度。

定义1：规则A⟹B在事务集D中成立，具有支持度S(support)，S是D中包含A∪B的事务数与所有事务数之比，记为support(A⟹B)，它等于事务包含集合A和B的并的概率P(A∪B)。即

support(A⟹B)=P(A∪B)=D(X)/|D|

(5)

其中，D(X)是数据集D包含X的事务数。

定义2：规则A⟹B在事务集D中的置信度C(confidence)是指包含A和B的事务数与包含A的事务数之比,它是条件概率P(A|B)。即

confidence(A⟹B)=P(A|B)=support(A∪

B)/support(A)

(6)

关联规则挖掘首先要找出所有满足最小支持度的项集，再计算出置信度大于阈值的所有关联规则。

2.2 FP-growth算法

FP-growth算法主要是利用一个树型结构来存储数据项之间的顺序关系，它通常需要扫描两次数据库来构建FP-tree，第一次扫描获得频繁1-项集，并筛选出满足支持度大小的频繁项，根据频繁项的支持度计数进行从高到低的排序。第二次扫描数据库就是按照第一次的频繁项排序对原始事务中的数据项重新排序，并将其添加到以“NULL”为根节点的FP-tree中。在构建FP-tree的过程中，通常会建立一个项头表T，表中包括三部分信息，分别是频繁项、对应的支持度计数和指向FP-tree节点的指针。根据FP-tree提取出条件模式基，满足置信度阈值的条件模式基和后缀就是挖掘出的关联规则。

FP-growth算法主要由三个模块构成：FP-growth模块主要是FP-growth算法执行的流程；Insert模块主要完成FP树的构建过程；Search模块用来获取条件模式基集合，该条件模式基集合可以用来确定最后的关联规则。

(1)Insert模块。

输入：已排序的频繁项集Li，FP(子)树根节点Rr

输出：FP(子)树Rr

IfLi!=null then

取出Li的第一项i

IfRr存在某子节点N=ithen

++N.count

Else

创建Rr的子节点N,节点内容为i

N.count=l

将N加入项头表中

Insert(Li-1,N)

(2)Search模块。

输入：FP树T,后缀模式α

输出：频繁项集合L_S

IfT中只有一个分支Pthen

ForP上节点的每个组合β

β=α∪β

L_S=L_S∪{β}

Else

ForT中的每个频繁项i

构造β的条件模式及条件FP树Rβ

IfRβ≠∅ then

Search(Rβ,β)

(3)FP-growth模块。

输入：事务集合T，最小支持度min_sup，最小置信度min_conf

输出：强关联规则集合R_S

扫描T找出频繁1-项集L

按支持度计数降序排序L

创建FP树的根节点NULL

ForT中的每个事务t

找出t中的频繁1-项集合Li

Li中的项按L中的顺序排序

Insert(Li,NULL)

L_S=Search(FP,NULL)

在L_S中产生强关联规则集合R_S

接下来用一个简单的例子解释如何构建FP树。假设存在事务集合T，如表1所示。假定min_sup=20%，那么事务集支持度计数=20%×10=2次。首先扫描一遍事务集，统计各类项的支持度计数，去掉支持度计数小于2的项。然后将频繁1-项按照支持度计数从高到低排序，生成排序的频繁1-项集L1=[B:8,A:7,C:5,D:2,E:2]。

表1 事务集合T

根据排好序的频繁1-项集集合创建项头表，然后再遍历一遍数据库，构建FP树。构建过程按照L1中项的顺序创建，将频繁项按照顺序插入到以NULL为根节点的树中，随着事务中数据项的插入更新各个树节点的支持度计数。根据Insert算法，遍历所有事务之后得出图1所示的FP-tree。故FP-growth算法是将事务中所有符合要求的项、项的计数以及项之间的相互关系都压缩到一棵树中。

图1 FP树与项头表

3 基于SOM划分的FP-growth算法

3.1 算法过程

FP-growth通过构造FP-tree来寻找频繁模式，然而当数据集达到一定规模时，构造基于内存的FP-tree仍然是不现实的。文中提出的基于SOM划分的FP-growth算法能解决上述问题。该算法利用SOM聚类方法得到信息较为聚集的数据子集，在各个子集上并行实施FP-growth算法，从而在大型数据集上挖掘出关联规则。该算法总体分成5步:数据标准化；按照系统抽样的方法从数据集中抽取样本数据；利用SOM算法对样本数据聚类，得到数据集事务的分类模型；将整个数据集中的事务按照分类模型分成若干个数据子集，在数据子集上并行执行FP-growth挖掘；汇总结果。算法流程如图2所示。

(1)数据标准化。

数据集中的每条事务中包含的项都是离散的，为了便于求解事务之间的欧氏距离，需要把事务中的项改为用数字表示，含有对应的项记为1，不含的记为0。具体过程如下：

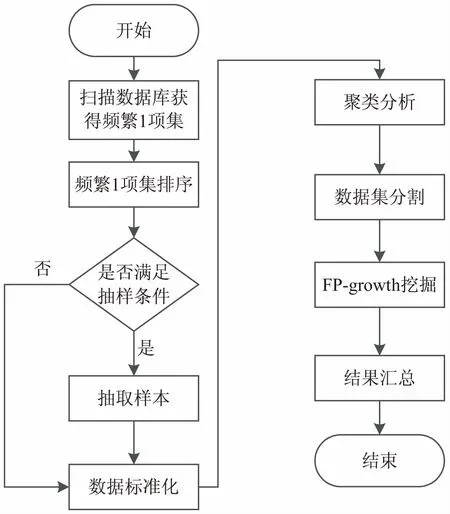
图2 算法流程

(a)扫描一遍数据集，求出数据集中大于支持度的频繁1-项集L1；

(2)抽取样本。

(a)将数据库D中事务编号，每条事务对应一个唯一的编号；

(b)将编号按某个间隔分成k段,当N/n(N表示数据集中的总的事务数,n表示样本容量大小)是整数时，k=N/n；当N/n为小数时,从总的事务中去除一些事务,使剩下的事务数目能被n整除,这时k=N'/n(N'为剩下的事务数)；

(c)在第一段中随机确定一个编号l;

(d)从整体中按照编号l,l+k,…,l+(n-1)k抽取出来作为样本。

(3)聚类分析。

利用SOM算法对样本数据进行聚类分析，经过若干次迭代运算，得到自组织神经元间的距离数据，神经元之间距离小的为同一类，距离大的为不同类。神经元在二维平面上的分布情况很容易通过肉眼大概分辨出数据集中存在几类数据。类别个数可以根据需要而定，一般情况下分得精细度越高，数据集中的类别数越多。文中在实验验证阶段，依次提高数据划分的精确度来验证算法的加速程度。确定分类个数后，利用点集最小圆覆盖法[12]确定每个类别的中心位置，得到中心位置集合：

C={c1,c2,…,cn}

(7)

其中，n为分类的类别数。

C中任何一个元素ck表示如下：

ck={ck1,ck2,…,ckm}

(8)

其中，m为中心坐标点的维数。

(4)FP-growth挖掘。

将数据集中的每条数据与C中的中心点进行比较，距离最小的中心点所属的类别就是该条数据所属的类别，即：

‖ti-cmin‖=min{‖ti-ck‖}

(9)

其中，ti表示任意一条事务数据；cmin表示与ti最近的中心点；ck表示C中任意一个中心点。

根据事务ti所属的类别将其分配到对应的计算节点上，这个分配过程在分布式计算Spark框架内完成，在Spark平台上编写的数据分配程序依据事务数据与中心点的欧氏距离来分配数据所属计算节点，详细的Spark平台的搭建和配置过程可参考文献[13]。经过数据分割后,数据集D被分割成s个子集，表示为D=D1∪D2∪…∪Ds。

在每个计算节点上构建FP-tree，构建过程按照2.2节的算法。由于这个阶段之前已经得到频繁1-项集，并且该项集已按照支持度从大到小排序，所以只需将每条事务中的项添加到FP-tree上即可。

(5)结果汇总。

(a)在每个计算节点上，根据2.2节的Search()算法求出所有条件模式基；

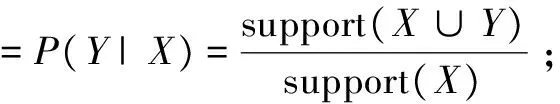
(c)将(b)中得到的关联规则合并就得到了整个数据集中蕴含的关联规则。由于之前做了SOM聚类分析，所以每个数据子集上包含有相应类别的高密度频繁项，那么也就包含了对应的关联规则。假设数据集D中包含的关联规则集R={r1,r2,…,rn}(n表示数据集中包含的关联规则个数，ri表示任意一条关联规则)，任意一个数据子集所包含的关联规则集RDi={rDi1,rDi2,…,rDim}(i=1,2,…,n，m表示子集中包含的关联规则的个数，rDij表示子集中任意一条关联规则)，则有：RD1∪RD2∪…∪RDs=R={r1,r2,…,rn}。

3.2 算法复杂度分析

假设某挖掘任务中有s个关联规则、m个符合最小支持度的项，事务有n个、平均每个事务中包含a个符合最小支持度的项。那么经典算法获取s个关联规则，忽略连接数据库等开销，算法需要计算的次数为m×n×a+m×s，由于n和m占主导作用，所以时间复杂度为O(mn)。假设抽取样本的个数为b，聚类个数为c，改进算法的时间复杂度为m×n×a+m×s+c×b，由于b和c相较于其他项很小，可以忽略不计，所以时间复杂度也为O(mn)[14-15]。虽然改进算法与原算法的时间复杂度相同，但是由于改进算法将数据库分割成小的子集，大大降低了算法的空间复杂度，减小了计算过程中的内存空间占用量，增大了对海量数据挖掘的可能性。而且在改进算法中各个子集并行进行数据挖掘，也大大缩减了运算时间。

4 实验及结果分析

通过实验对提出的基于SOM划分的FP-tree算法进行验证。实验中的数据集均来自Frequent Itemset Mining Dataset Repository。

4.1 SOM聚类分析结果

实验中使用的是connect.data数据集。对该数据集进行抽样，对抽样样本进行SOM聚类分析，经过100次迭代后，二维平面上的神经元出现了聚簇，相似的神经元相互靠近，不同类的神经元相互远离。每个神经元都与某些输入点有着强连接，并且神经元之间也存在着连接权值，将距离较近的神经元归为一类，它们对应的样本点也属于同一类。

为了凸显聚类效果，在每一个类别上加入一个收缩因子，在收缩因子的作用下样本点向各自的数据中心靠拢。为了更直观地看到分类效果，在每个类别上分别标记不同的图形：三角形、方形、菱形和圆形。经过多次调整参数，得到的聚类效果如图3所示。由于这个过程需要比较复杂的编程，所以利用Java程序编程实现聚类的效果显示。

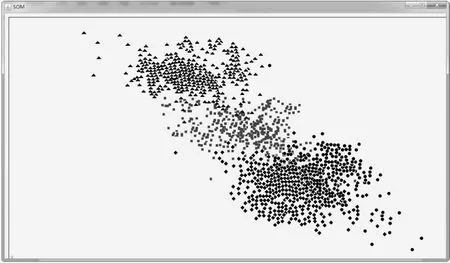
图3 聚类效果

从图中可以看出，经过SOM聚类分析，样本数据分成了4类，虽然每个类别有一些数据相互重叠，但是总体上并不影响最后的聚类效果。

4.2 基于SOM划分的FP-growth算法性能实验

根据4.1中的聚类结果，将原数据集分割成4个子集，在每个子集上并行执行FP-growth算法。算法执行过程中单个计算节点的内存占用情况如图4(a)所示。图4(b)显示的是未改进的FP-growth算法执行过程中的内存占用量。图4中显示的是加上计算机操作系统和其他进程所占的内存空间后的内存使用情况，并且是以60 s为一个时间片段显示的。通过比较发现，改进算法内存占用量远远低于未改进算法，可以用来对大型数据集进行数据挖掘，而未改进的FP-growth在对大型数据集进行挖掘时，很快就会占用大量内存，以至于计算机物理内存空间不够造成数据挖掘任务无法继续进行。

图4 内存占用量

将改进算法与Apriori算法和FP-growth算法进行速度上的比较，在支持度为5%的情况下，各个算法的运算时间如图5所示。

从图中可以看出，随着数据量的增加，三种算法所消耗的时间都在增加，然而FP-growth算法的时间消耗明显低于Apriori算法，主要因为随着数据量的增大，Apriori算法会产生大量的候选项，这些候选项的处理耗费了大量时间。改进的FP-growth算法相较于没有改进的FP-growth算法明显降低了算法的运算时间。从图中可以看出,未改进的FP-growth算法随着数据量的增加所消耗的时间也在快速增长，而改进的FP-growth算法呈现平缓的增长趋势，由此可见改进算法在性能上有明显的提升。

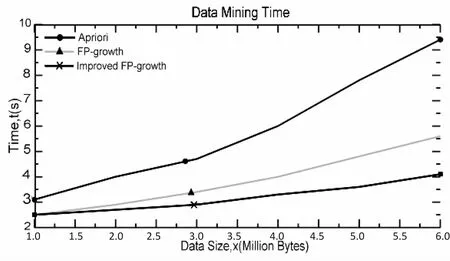
图5 执行时间对比

5 结束语

主要阐述了对FP-growth算法改进的过程。该算法利用SOM聚类算法对从大数据集中抽样的样本进行聚类分析，根据聚类结果将大数据集分解成若干个子集，这些子集具有较高密度的关联规则，在各个子集上并行执行FP-growth算法就得到了数据集中所包含的关联规则。实验结果表明，改进算法降低了内存的占用率，缩短了数据挖掘时间。

参考文献:

[1] AGRAWAL R,IMIELINSKI T，SWAMI A.Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACM-SIGMOD international conference on management of data.New York,NY,USA:ACM,1993:207-216．

[2] AGRAWAL R,SRIKANT R.Fast algorithms for mining association rules[C]//Proceedings of the 1994 international conference on very large data bases.[s.l.]:[s.n.],1994:487-499.

[3] HAN J,PEI J,YIN Y.Mining frequent patterns without candidate generation[C]//Proceedings of 2000 ACM SIGMOD international conference on management of data.New York,NY,USA:ACM,2000:1-12.

[4] 杨 勇,王 伟.一种基于MapReduce的并行FP-growth算法[J].重庆邮电大学学报:自然科学版,2013,25(5):651-657.

[5] PARK J S,CHEN M,YU P S.Using a hash-based method with transaction trimming and database scan reduction for mining association rules[J].IEEE Transactions on Knowledge and Data Engineering,1997,9(5):813-825.

[6] 吴建章,韩立新,曾晓勤.一种基于多核微机的闭频繁项集挖掘算法[J].计算机应用与软件,2013,30(3):44-46.

[7] AOUADL M,LE-KHAC N A,KECHADI T M.Distributed

frequent itemsets mining in heterogeneous platforms[J].Journal of Engineering,Computing and Architecture,2007,1(2):1-12.

[8] 邹 翔,张 巍,刘 洋,等.分布式序列模式发现算法的研究[J].软件学报,2005,16(7):1262-1269.

[9] 李文栋.基于Spark的大数据挖掘技术的研究与实现[D].济南:山东大学,2015.

[10] 王 乐,冯 林,王 水.不产生候选项集的TOP-K高效用模式挖掘算法[J].计算机研究与发展,2015,52(2):445-455.

[11] GOETHALS B,MOHAMMED J Z.Advances in frequent itemset mining implementations:report on FIMI'03[J].ACM SIGKDD Explorations Newsletter,2004,6(1):109-117.

[12] 杨中华.平面点列最小覆盖圆的计算方法[J].北京工业大学学报,2000,26(2):96-97.

[13] 毛宇星,施伯乐.基于扩展自然序树的概化关联规则增量挖掘方法[J].计算机研究与发展,2012,49(3):598-606.

[14] HAN J W，MICHELINE K．数据挖掘:概念与技术[M].范明，孟小峰，译.北京:机械工业出版社，2012.

[15] 易 彤,徐宝文,吴方君.一种基于FP树的挖掘关联规则的增量更新算法[J].计算机学报,2004,27(5):703-710.