直线超声波电动机精密定位系统位置精确控制

毛新丰，孙志峻，姚志远，冒娟娟

(南京航空航天大学，江苏南京210016)

0 引 言

随着当前精密工程若干领域的快速发展，对其关键技术之一，精密定位技术的需求也日益增长。它要求系统具有微米级(甚至是纳米级)的重复定位精度及分辨率。现有的定位技术中，常选用“伺服电机+滚珠丝杠”的方式，由于有运动转换环节，不可避免存在间隙误差，再加上长时间运转造成的机械磨损，其定位精度受到很大限制［1］。

直线超声波电动机是利用压电元件的逆压电效应和弹性体的超声振动，通过定子和动子之间的摩擦作用，把弹性体的微幅振动转换成动子宏观的直线运动，直接推动负载，因其响应快、断电自锁、无需运动转换机构，故其定位和速度控制精度高，可达到纳米级［2］。将其应用于精密定位平台，可获得较高的定位精度及分辨率，在精密工程中具有非常重要的意义。本文针对直线超声波电动机驱动的精密定位平台，采用光栅编码器作为位置反馈传感器，DSP为核心控制器，LabVIEW作为上位机开发软件，搭建起了完整的精密定位闭环控制系统，设计探讨了适合超声波电动机的控制方法，并进行了深入的实验研究。

1 精密定位系统的构成

文中的精密定位系统由直线超声波电动机、直线导轨、超声波电动机驱动器、TMS320F2812DSP及外围电路、光栅编码器、上位机硬件和软件六部分组成。精密平台的外观图如图1所示，直线超声波电动机由丝杆螺母传动机构夹紧，与直线导轨联接并稳定固定在工作平面上。

图1 直线精密平台外观图

本文选用的位置反馈传感器是美国GSI公司的Mercury II 4800增量式光栅编码器，其分辨率可通过内置Smart Precision软件进行设置，最低为5 μm/count，最高可达1.22 nm/count，输出 A+/A－、B+/B－、Z+/Z－三路差分信号，能较好地抑制共模干扰，提高系统的位置检测精度。为将编码器的差分输出转换成单端脉冲信号，笔者选用26LS32AC差分转单端芯片搭建了差分信号处理电路。

在核心控制器方面，TI的F2812DSP片内集成了大容量的Flash存储器和两个功能强大的事件管理器，其独有的正交编码脉冲电路可实现与光栅编码器的无缝对接［3］。此外，该芯片既具备数字信号处理器特有的强大数据处理能力，又像单片机一样针对控制应用在片内集成了丰富的外设模块和扩展接口，因此非常适合作为本系统的核心控制器，来完成各种算法和控制流程，并与上位机通讯。

除了传感器与控制器的合理选择外，直线精密平台要获得很高的定位精度，对其运动速度也必须进行严格的控制。本文通过外扩D/A芯片，使DSP产生可控的直流电压，施加在电机驱动器的压控振荡器上来实现电机调速，选用的是美国模拟器件公司(ADI)的AD558。

为了控制方便及实现人机交互，本文以Lab-VIEW开发上位机(PC)界面，如图2所示，用户可输入直线平台的目标位置，使其从当前位置连续运动到指定位置，此外，还添加了直线平台的初始归零和手动步进。PC机通过RS232串口将控制命令和运行参数下传到DSP后，直线平台的运行就由DSP来实时控制，与此同时，DSP将每次采样得到的平台位置信息回传到上位机，PC机将显示直线平台的位置和速度(通过微分运算得到)曲线［4］。精密定位系统的总体结构如图3所示。

2 精密定位系统控制分析

本文中直线超声波电动机精密定位系统的控制目标有3个:一要保证平台准确地运动到用户指定的位置;二要保证平台在其运动过程中平稳;三是在前两点的基础上实现平台到达目标位置的快速性。

超声波电动机的驱动原理是建立在压电元件的超声振动力和机械摩擦力的基础上的，这使得超声波电动机的模型非常复杂，而且电机的性能随工作温度、负载、运动速度、运动方向及定子动子间压力的变化而变化。因此，超声波电动机的控制特性复杂且具有强非线性［5］。

最近几年，模糊规则、神经网络和自适应控制方法备受青睐。借助人的经验，模糊逻辑控制可以补偿系统的非线性，然而，它过多依赖设计者的直觉和经验。自适应控制可以自我调节控制器的参数来适应系统的变化，但是它往往需要系统的参考模型，这对超声波电动机来说是不实际的。神经网络控制可以处理系统复杂的非线性问题，但是它需要较长的训练和收敛时间［6］。这些研究成果都很难应用到本系统上。

PID控制是连续系统控制理论中技术最成熟且应用最广泛的一种控制技术。当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，应用PID控制技术最为方便，调节PID的参数，可实现在系统稳定的前提下，兼顾带载能力和抗扰能力，具有较宽的稳定裕度［7］。本文结合超声波电动机的控制特点，以PID控制为基础，对直线超声波电动机精密定位系统进行位置精确控制的深入研究。

3 闭环控制方法及实验研究

PID控制器在时域中的模拟算法如下:

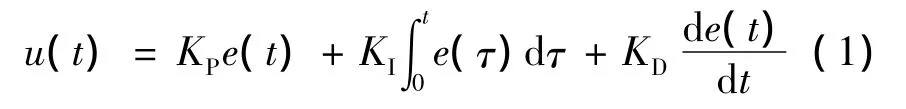
式中:e(t)为误差信号;u(t)为控制信号;KP为比例系数;KI为积分系数;KD为微分系数。

在直线超声波电动机精密定位系统的位置反馈控制中，u(t)是加在驱动器压控振荡器上的模拟直流电压，e(t)是目标位置与当前位置的差值。将式(1)离散化，可得到数字形式的PID控制规律:

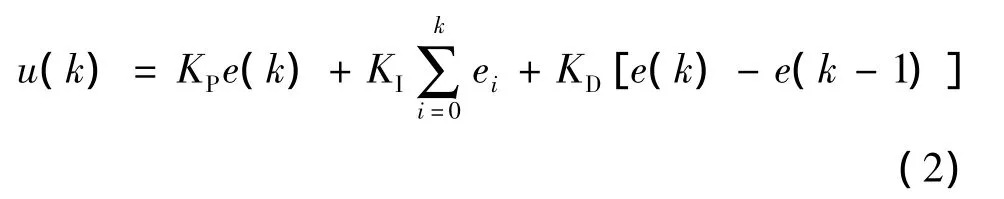
此算法需利用系统偏差的累加值∑ei，随着采样数k的增加，累加的项次也依次增加，这不利于DSP 计算。为此，采用增量式 PID 算法［8－9］:

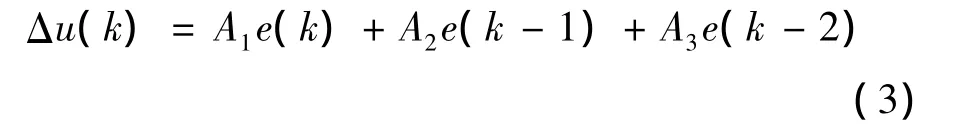
式中:A1、A2、A3三个系数可以根据用户设定的KP、KI、KD预先算出，A1=KP+KI+KD，A2=－(KP+2KD)，A3=KD，从而加快了算法程序的运算速度。由此，可以得到直线超声波电动机精密定位系统电压控制量的表达式:

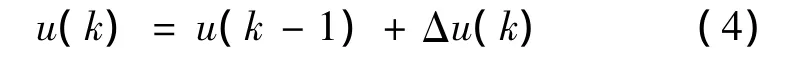
针对本系统，PID控制回路框图如图4所示。

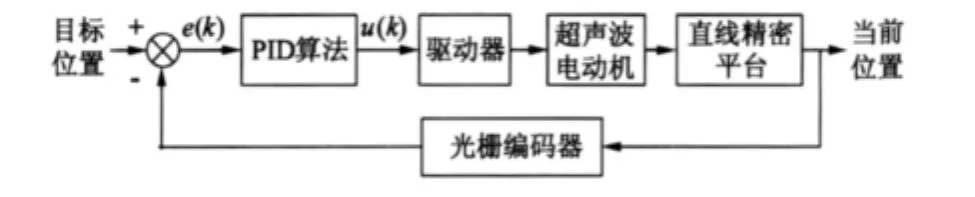
图4 PID控制回路框图

图5为直线平台在PID连续控制下的位移和速度曲线，比例、积分和微分参数通过试凑法找到控制效果较优的一组，分别为10、2、6，控制器的采样周期为 5 ms，传感器的分辨率设为 2.5 μm/count。从位置曲线可知，平台的起始位置在－6 195.0 μm处，目标位置为－3 000.0 μm 处，实际运行到－2 947.5 μm 处，定位误差达到了 52.5 μm，且电机在目标位置处经过两个振荡后才停止，有明显的超调。从速度曲线可知电机的起动时间约为30 ms，关断时间约为10 ms，电机起动时速度有波动，在目标位置附近速度正反交替，没达到理想的平缓要求。这说明单纯的PID控制无法实现精密定位系统控制目标。

图5 直线平台在PID连续控制下的位移和速度曲线

究其原因，虽然超声波电动机相比于普通电磁电机响应要快，且断点自锁，但在连续运动的状态下，加上平台负载的惯性影响，其停止时的惯性位移达到了50 μm左右，大大超过了系统所要求的精度范围，因此在单纯的PID连续控制下，在目标位置处不可避免地产生了连续振荡，平台的定位误差也远远超过了要求的精度，停止时的速度也很难达到平缓。

为了消除单纯PID连续控制的缺陷，笔者想到了利用超声波电动机微小步进运动的特点，结合PID控制，来实现精密定位系统的控制目标。从图5的位置和速度曲线可知，电机在起动过程中，起动时间越短，平台的位移越小，速度也越低，若在PID调节的低速阶段实行微小步进运动，则将充分发挥直线超声波电动机运行高分辨率的优势。而在实际应用中，直线超声波电动机在极短起动脉冲下是能达到纳米级位移的。经过多次微小步进试验，笔者获得了平台在低速时不同起动脉冲下的步进距，达到了微米级甚至纳米级，如表1所示。

表1 电机在不同起动脉冲宽度下的步进距(多次平均值)

显然，采用微小步进控制超声波电动机不适用于长行程的运动，但非常适合在逼近目标位置时的精确定位控制，笔者融合了微步控制的思想，如图6所示，在电机运行到目标位置前80 μm附近预停，待其经历一段惯性位移，再在之后的每个采样周期内实行微步控制，步进距根据当前误差的大小来决定，此时，电机已处于PID调节的低速阶段，越逼近目标位置，速度越低。程序对最终平台是否在目标位置的精度范围内进行了多达20次的判定，直到判定成功，才停止采样，重返接收上位机命令处，这样做是为了充分保证平台精度的稳定。DSP程序中运动控制算法的流程图如图7所示。

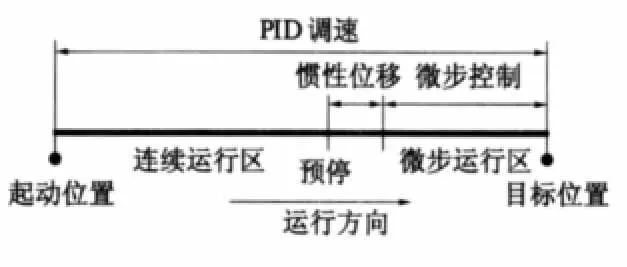
图6 直线精密平台定位示意图

图7 系统控制算法流程图

图8为基于PID连续控制+微步控制的直线平台位移和速度曲线，比例、积分和微分参数分别为10、2、8，控制器的采样周期为 6.4 ms，传感器的分辨率设为0.5 μm/count，实验在恒温恒湿的超净实验室中完成。从位置曲线可以看出，平台的起始位置在－1 969.5 μm 处，目标位置为 +530.5 μm 处，平台在距离目标位置16 μm处开始步进运动，经过50 ms左右的时间(监测到8个步进)，最终准确地到达了目标位置，利用激光干涉仪检测到的实际位移为 2 499.6 μm(目标位移为2 500.0 μm)，定位误差0.4 μm在编码器设定的位移分辨率(0.5 μm)以内，且电机没有明显超调，缓慢地逼近目标位置。从速度曲线可以看出，整个运行过程仅用时140 ms左右，且平台在逼近目标位置时速度平缓，没有波动，非常理想。

图8 基于PID连续控制+微步控制的直线平台位移和速度曲线

表2为直线精密平台在不同行程下的重复定位精度，平台的定位误差控制在0.5 μm以内。可见，在PID连续控制和微步控制的联合控制下，直线平台达到了所要求的控制目标，即准确、平稳和快速，且具有很好的重复定位精度。

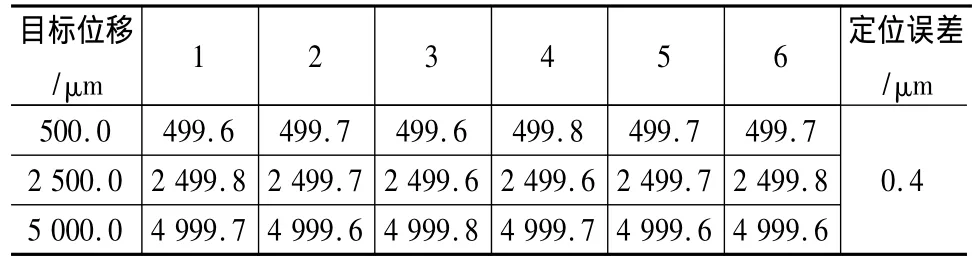
表2 直线精密平台重复定位精度

4 结 语

本文针对基于直线超声波电动机的精密定位平台，建立了一个完整的闭环控制系统，利用 Lab-VIEW开发了操作简便的人机界面，采用F2812DSP作为下位机实时控制平台的运行，并通过RS232串口建立了上、下位机通讯，集人机交互、数据采集显示和位置精确控制于一体。平台位置精确控制方面，研究发现在单纯PID控制下，由于平台连续运动的惯性位移达到50 μm左右，使得其在目标位置附近产生连续振荡，定位误差也较大，无法达到理想的控制目标。本文结合超声波电动机的控制特点，借助其在极短脉冲激励下运行高分辨率的优势，将微步控制的思想融入PID控制中，最终使系统达到了较好的控制品质，实现了平台运行准确、平稳和快速的控制目标。所进行的闭环阶跃响应实验表明，在0.5 μm光栅精度的控制中，直线平台在不同行程下的重复定位精度保持在0.5 μm以内，且平台运行平稳，无超调。

［1］欧阳航空，陆林海，侯彦丽.精密定位平台的系统误差分析及螺距误差补偿方法的实现［J］.机电工程，2005，22(1):22－26.

［2］赵淳生.超声电机技术与应用［M］.北京:科学出版社，2007.

［3］韩丰田.TMS320F281x DSP原理及应用技术［M］.北京:清华大学出版社，2009.

［4］Bishop R H.LabVIEW 8实用教程［M］.北京:电子工业出版社2008.

［5］孙志峻，邢仁涛，赵淳生，等.超声电机驱动多关节机器人位置精确控制［J］.应用科学学报，2007，25(5):493－499.

［6］Chau K T，Chung S W.Neuro－fuzzy speed tracking control of traveling－wave ultrasonic motor drives using direct pulsewidth modulation ［J］.IEEE Transactions on Industry Applications，2003，39(4):1061－1069.

［7］高钟毓.机电控制工程(第2版)［M］.北京:清华大学出版社，2002.

［8］张晓，王晓宇，郭涛，等.增量式PID规律在电机软起动控制中的应用［J］.机电一体化，2008，10(12):57－59.

［9］邢仁涛.超声电机驱动多关节机器人的设计与控制［D］.南京:南京航空航天大学机电学院，2006.