基于参数回归模型的异步电动机等值电路参数测定
林友杰,谢卫才
(湖南工程学院,湖南湘潭411101)
0 引 言
异步电动机等值电路参数的准确性一直以来都是受到特别关注的问题,也是电机高精度控制必不可少的前提条件。等值电路参数计算的传统方法是通过空载实验、堵转实验以及直接测量定子绕组电阻实验和大致估算短路漏抗中的定转子漏抗分配比例(一般取为相等)来计算出等值电路参数的[1]。
传统异步电动机参数测定实验及其处理方法是在近似处理的基础上建立的。如忽略铁耗等效电阻,堵转时s=1,实际运行时一般a<5%,两者工况不同,由于转差频率差别大而使得通过短路实验所测的转子电阻与实际电机运行的转子电阻值不相符;又如数据处理上引入的误差,等值电路参数计算的传统方法是通过空载实验、堵转实验以及根据异步电动机的几种常见类别大致估算短路漏抗中的定转子漏抗分配比例来计算出等值电路参数的。
电气工程界,针对电机参数测定的不准确性,采取的措施主要有以下三种[2-8]:
(1)研究更好的实验方法及数据处理的方法。
(2)利用在线识别参数的技术来得到更符合实际运行时的参数值。
(3)利用模糊控制等控制方法来减弱或撇开对电机参数的依赖性。
文献[2]研究了更准确的计算模型,利用直接求解方程组的方法得出了更准确的电机参数,但在构建方程组时由于受方程组本身特性的影响,采用了由空载、短路和负载实验数据组成方程组,虽然较传统的方法更准确,但由于电机运行时的参数与空载、短路时的参数值有所不同,参数处理精度还可以提高。
本文从参数回归模型入手,利用异步电动机的负载实验数据,利用在优化拟合方面功能强大而又简单易用的1stopt软件来研究电机参数更准确的处理方法。
1 参数回归模型
异步电动机的等值电路表现出8个参数,Rs、Rr、Rm、Lls、Llr、Lm及 s、ω,后两者与运行条件相关,是外部参数,通过简单计算即可得到,其中ω为给定电源的频率,s为转差率,通过ω和转速来求取(图1,转子侧参数是已折算到定子侧的值)。其它6个参数为异步电动机等值电路的基本参数,是通过实验直接测定或其它方法间接求取的对象。
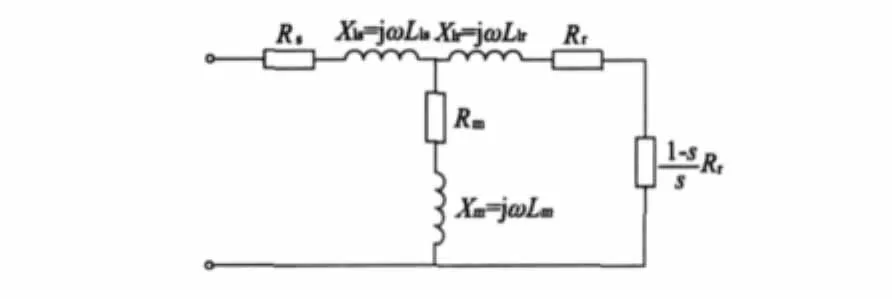
图1 异步电动机等值电路
从图1可知,等值电路的输入阻抗:
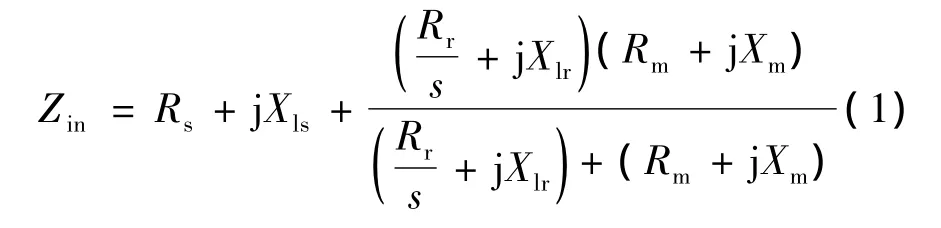
进一步推导可得关于输入阻抗的实部和虚部的2个方程:
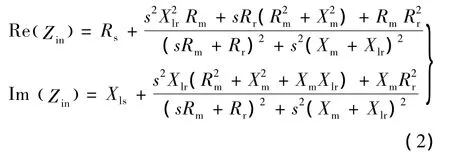
式中:Zin为定子侧输入阻抗,Re(Zin)、Im(Zin)为求Zin的实部、虚部运算。
从电路的观点看,输入阻抗的实部和虚部所消耗的功率分别为有功功率和无功功率。这两部分的功率可以通过功率表、电压、电流表测出,在忽略电机的机械损耗的基础上,其值分别为:

式中:Pin、Us、Is为异步电动机参数测定实验时的输入功率、定子线电压、线电流的测量值。ω为电源角频率,ω=2πf,f为输入电源的频率,转差率s通过下式计算:

式中:p为电机极对数;n为电机转速。式(3)就是异步电动机等值电路参数回归模型,为了计算方便,改写如下:

式中:

式(5)是异步电动机参数回归模型(式(3))的计算模型,回归模型的输入为s、x、y,待回归的参数为异步电动机的各电阻、电感的量值。在回归模型中采用电抗而不是电感作为求解参数,因为考虑到异步电动机中的电抗比电感在数值上更接近于电阻,在非线性方程组上更易于求解。
2 回归模型的直接求解
利用参数的回归模型以及异步电动机的负载实验数据值,可以求出负载时的异步电动机等值电路的参数值。样机YLEWF-6三相异步力矩电机的负载实验数据如表1所示。由式(4)、式(6)可以得出参数回归模型(式(3))所需的 s、x、y值数据,如表2所示。

表1 负载试验数据汇总(定子绕组星形联结)

表2 参数回归模型的数据
将s、x、y作为变量,利用1stopt进行回归计算得出待拟合的参数值。
数据处理结果如表3所示。

表3 直接回归方式的参数值和精度
从表3可以看出,回归的相关系数达到了0.999 8,接近于1。从实际的物理情况看,转子侧不可能没有漏磁通/漏磁链,因此对应的漏抗值就不可能为0。参数中除了转子的漏抗与实际不符外,其它参数的大小及各参数之间的数量级大小关系符合实际的电机情况。
这个误差是由定子电流、输入功率的测量精度以及x、y的计算精度、回归方程的非线性等引起的。可以将这些影响因素归结为对s的影响,即认为s的数据是准确的,而将所有的误差加在转差率s上。
因此从某种意义上讲,可以用变转差率s(回归中修正的s值)方法进行回归拟合,以提高拟合的准确性。借助ParVariable关键词,1stopt可以完成这一过程[9]。
对应的变转差率s回归方法的回归结果如表4所示。

表4 变转差率s回归方式的参数值和精度
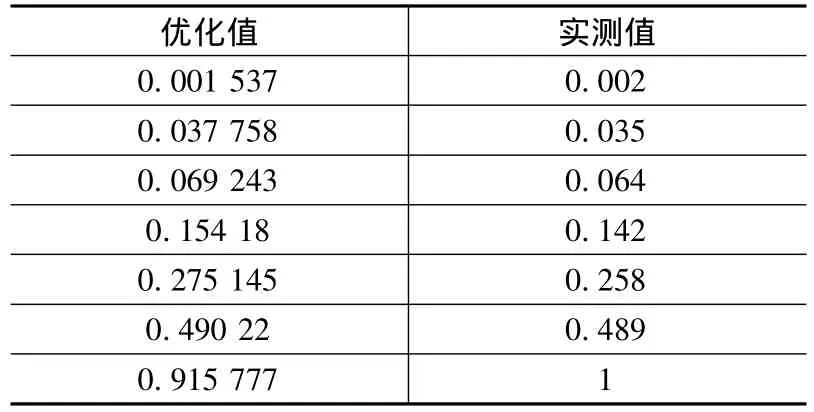
表5 转差率的优化值和实测值
表4为变转差率s回归方式的参数值和精度。表5的第1列数据为变转差率回归中的转差率优化值,表5的第2列数据为负载实验的转差率实际值。
从表4和表5可以看出,将误差的影响集中放在转差率来考虑而带来的转差率的偏差值不大。但转子侧参数的回归值有了明显的改善(特别是转子漏电阻),与定子侧的数值相接近且在同一数量级上,这更符合异步电机参数值实际物理情况。是否更接近被测电机的实际参数值,要通过进一步的方程组特性研究和更多的实验才能得到验证,这步工作尚需深入。
3 带约束条件的回归模型的参数求解
IEEE Standard 112标准中给出了几种类别的异步电动机的定转子漏抗(漏感)的推荐值[1]。根据该标准,若大致知道异步电动机的定转子漏抗比,就可以进行带约束条件的回归模型的参数求解。
根据力矩电机的定转子漏抗参数的分配比例,可得约束条件:

表6为带约束条件的回归模型所得出的异步电动机的等效电路参数值及对应的回归精度。

表6 带约束条件回归的参数值和精度
从表6可以看出,加入了约束条件,等值电路的参数值符合力矩电机参数值情况。带约束条件的回归方法与变转差率s的回归方法(表7)相比,可以很明显地看到,拟合精度稍逊于后者,电机等值电路中的定子电阻值明显比后者大,而励磁电阻要明显小于后者。
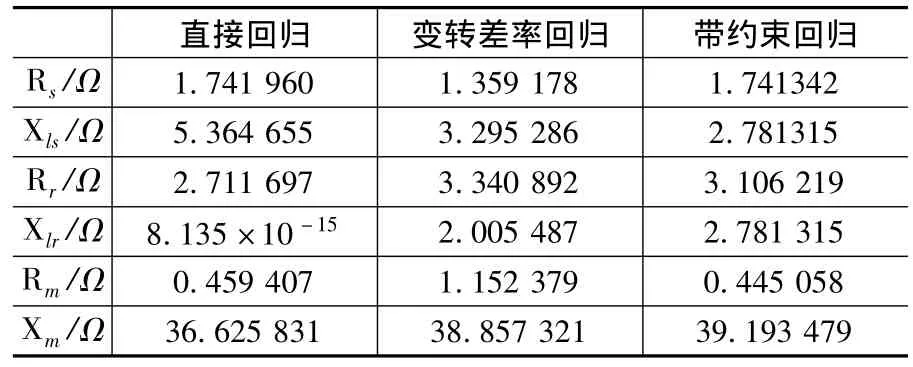
表7 3种回归方式的结果比较
4 验 证
已知样机YLEWF-6三相异步力矩电机的冷状态下直流电阻测量值如表8所示。

表8 直流电阻测量结果汇总
将定子绕阻平均相电阻值换算到标准工作温度75℃下:

式中:对于铜导线T=225。
定子绕组的电阻除了与温度有关外还与所通入的电流频率有关。由于集肤效应的影响,同一绕组交流电阻值要稍大于直流电阻值。因此实际负载时的定子绕组的电阻值在式(8)的附近变化。假定变化范围为±10%,则有:
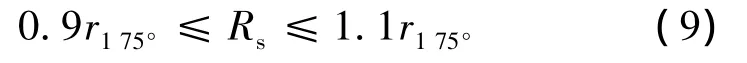
代入数值得:
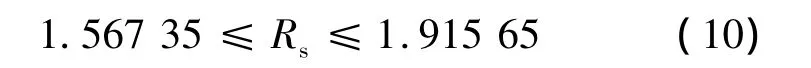
由式(10)可以看出,第3种的拟合方法得出的定子电阻值最合理。其它参数的大小比例关系也符合力矩电机的实际物理情况,当然其它的数据的准确性还需进一步的验证。
也可以将式(10)作为约束条件放在回归模型中,从而得到更准确的参数值。
5 结 语
在忽略机械损耗的基础上,推导了异步电动机等值电路的参数回归模型,并由回归模型利用1stopt,探讨了可以快速简洁求出比传统方法更为准确的数值解的原理,并对几种参数回归方法进行了有益的尝试。文中回归的结果表明,忽略机械损耗的参数回归模型的回归结果不够理想,因此应该将机械损耗也作为一个待回归的参数加入到回归模型中,但这需要更大量的计算,要有好的算法或软件支撑。
实验数据处理的准确程度也有赖于数据测取的数量和精度,回归方法是在大量的观测数据中寻找变量之间内在的联系,因此文中所提出的三种拟合对电机对参数更准确测定有一定的应用价值和指导意义。在此基础上,可以进一步研究加权拟合/回归等算法以及变换改进回归模型来取得更好的拟合/回归效果,当然数据越多拟合的精度越高,也越符合异步电动机实际的等值电路参数值。
尽管是针对于异步电动机的参数测定的数据处理,但参数回归的方法也可以推广到变压器和其它类型的电机参数测定的数据处理中。
[1]Fitzgerald A E,Charles Kingsley,Jr.,Stephen D Umans.电机学(第6版)[M].刘新正,苏少平,高林,等译.北京:电子工业出版社,2004.
[2]林友杰,吴汉光.异步电机等值电路参数计算的一种新方法[J].福州大学学报(自然科学版).2006,34(4):512-515.
[3]冯浩,金阳,钟德刚,等.异步电动机等值电路参数高精度计算方法探讨[J].电机与控制应用,2001,28(3):1-6.
[4]董改花.三相异步电动机等值电路参数计算的综述[J].煤矿机械,2006,27(2):207-2010.
[5]尹文怡,范通让.电动机试验数据拟合算法的研究与实现[J].微电机,2009,42(3):93-95.
[6]李建军,盛洁波.异步电机定转子参数的辨识方法研究[J].电工技术学报,2006,21(1):70-74.
[7]张微,王长江.一种新型感应电机的参数自测定方法[J].大电机技术,2003(1):18-23.
[8]武建文,李德成.电机现代测试技术[M].北京:机械工业出版社,2010.
[9]七维高科有限公司.1stopt 3.0用户手册[M].2009.

