大规模散乱点云数据的曲率估算及计算机实现
王 伟,唐民丽,吴恒玉
(海南软件职业技术学院 电子工程系,海南 琼海 571400)
随着三维扫描设备的广泛应用,点几何元素受到越来越多的重视.对于复杂结构的模型,使用点集表示比三角网格更能有效地表示和显示该几何形体[1].以曲率为准则的简化算法,能够保留模型的特征,其绘制效率大大提高.另外,曲面模型重建得到越来越多的应用和研究,点云数据分片技术是其过程的重要环节.大多数分片技术采用点云上每个点的曲率作为曲面特征识别的重要依据.
点云数据的曲率估算方法,国内外已有一定的研究.Milroy[2]等采用局部坐标系内的二次参数曲面逼近点云,利用曲率的微分性在OCS(orthogonal cross section) 模型上估算点云数据的曲率值.Huang[3]等和刘胜兰[4]等是在三角网格模型上进行曲率估算.胡鑫等[5]采用了图像处理中的梯度求解法,对点云中每一点处的曲率进行估计,其对噪声没有抑制作用,同时对点云数据的组织方式有要求.Yang[6]等直接以点云模型为研究对象,但却局限于对规则点云进行曲率计算.这些方法都有其理论上的局限性,同时,对于大规模点云数据,由于曲率计算量庞大,普通的计算机难以实现.
本文改进了Yang的方法,直接在散乱点集模型上计算曲率.同时提出根据点云模型特征,进行区域划分,将整个点云数据划分为若干个部分,分别计算其曲率,从而在普通计算机上实现大规模散乱点云数据的曲率估算.
1 区域划分
对目标物体进行三维激光扫描后,能够得到物体的三维数据信息,即三维激光扫描的初始点云数据,而这些数据在三维空间里必然是一个有限的数据点集.如果用一个封闭的空间可以将这些点集包围起来,则称这个封闭的空间为原始点云数据的最外区域.这个区域形状、大小都可以根据点云数据的形状、大小来确定.对本文将要处理的隧道的点云数据,可以将其最外域选择为相对简单的形状,如长方体区域.
如果能找到原始点云数据中x、y、z轴方向上的最大值和最小值,就可以确定长方体区域的8个顶点的坐标(xmax,ymax,zmax)、(xmax,ymax,zmin)、(xmax,ymin,zmax)、(xmax,ymin,zmin)、(xmin,ymax,zmax)、(xmin,ymax,zmin)、(xmin,ymin,zmax)、(xmin,ymin,zmin),长方体最外域的范围也就确定了.
将原始点云数据的长方体最外区域确定之后,对这个区域进行细化,将它划分为一个个更小的区域.假设将长方体最外区域沿x、y、z轴方向划分成n×p×q个小长方体,如果小长方体的长、宽、高分别为a、b、c,就可以通过式(1)求得小长方体的个数为

对最外区域细化后的点云数据进行观察,可以发现每一个小长方体区域中可能会包含一个或者很多个点,有的甚至不包含点;但是每一个点只会被唯一的一个小长方体区域所包含.另外值得一提的是小长方体区域如果划分得越细,压缩的精度就越高;反之,压缩的精度就越低.
2 曲率估算
本文用二次参数曲面逼近点云来估算曲率,具体步骤如下:
1) 对点云进行空间划分和K邻近计算,把每个点xi的K邻近包括该点记为N(xi),每个N(xi)的隐含曲面用一个切平面逼近.N(xi)在切平面上的投影记做N(x'i),各点的切平面计算可以通过各点的邻近点关系和最小二乘原理[1]求得,且xi与x'i必须满足一一映射关系.
2) 以x'i为基点,求出距离xj'最远的点xj',xj'∈N(x'i).连接x'i,xj'两点的直线方向作为u方向,垂直于u方向的直线方向作为v方向.
3) 将N(x'i)的每一点都与x'i相连,得到k个有向线段,把这些线段在u方向上的投影记为di,1≤i≤j.将di进行排序,最大的记为dmax,最小的记为dmin,则N(x'i)每一点对应的u参数值为

式中:2≤j≤k+1;U1=0.
4) 为了计算每一顶点的曲率,运用Yang所形成的二次参数曲面逼近法求得较为精确逼近散乱数据点的二次参数曲面.利用顶点xi的N(xi)建立二次参数曲面

3 计算机实现
以激光三维扫描仪扫描的隧道点云数据为基础,运用Imageware和Matlab程序设计的方法实现对三维点云数据的处理.本文实验是在CPU coreTM2,内存2 G,硬盘250 G,Matlab 7.0.1和Imageware 12平台环境下进行的,点云数据数量为38 645.
具体实验步骤如下:
1) 启动Imageware逆向工程应用软件,打开三维激光扫描仪扫描后形成的.asc点云数据文件,原始点云数据显示如图1所示.
2) 使用Imageware打开点云信息对话框,可以方便地得到点云数据的基本信息,根据点云形状进行区域划分,选择长方形作为最外区域.区域划分如图2所示,长方形最外区域顶点坐标如表1所示.

图1 三维激光扫描原始点云数据

图2 原始点云数据长方体最外区域坐标
3) 最外区域细化.对本文要处理的点云数据,分析其特点后,初步设定小长方体区域的长、宽、高值分别为5、5、3,得到如表2所示的关于小长方体区域的数据.
4) 使用Matlab编程实现曲率估算.
实验结果表明,直接对点云做曲率估算,计算机会陷入死循环,无法得到曲率估算的结果.引入区域划分后,能快速得到曲率估算的结果,同时处理结果能满足后续工作的需要.
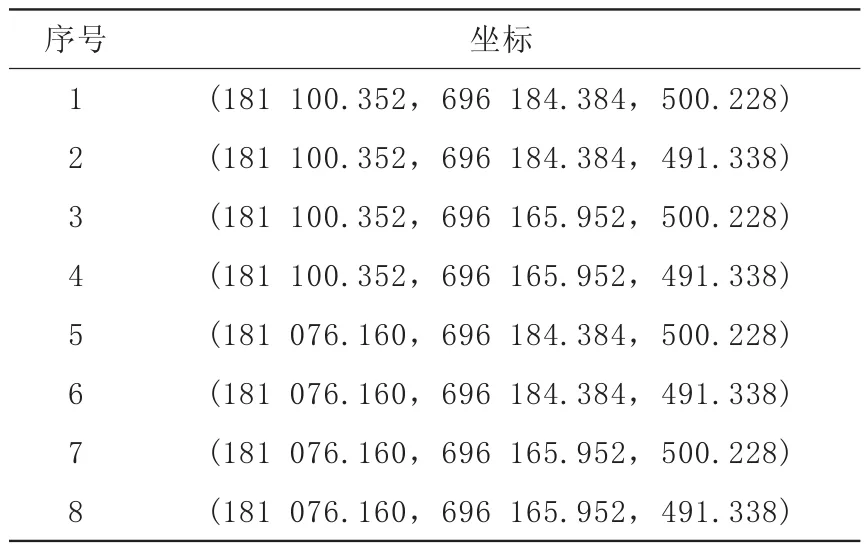
表1 长方体最外区域顶点坐标

表2 小长方体区域的边长与个数
4 结 论
对大规模点云数据进行区域划分后,可以在普通计算机上实现曲率估算.本文所采取的方法可以推广到任意形状的大规模点云数据的曲率估算,并不局限于点云的形状,这对在普通计算机上实现散乱点云数据的曲率估算具有重大的推广意义.
[1] PAULY M,GROSS M, KOBBELT L P.Efficient simp lification of point-sampled surfaces[C]//Proceedings of Visulization 2002.VIS 2002.IEEE.Boston: Is.n.I,2002: 163-170.
[2] MILROY M J,BRADLEY C,VICKERS G W.Segmentation of a wrap-around model using an active contour[J].Computer-Aided Design,1997,29(4):299-320.
[3] HUANG Jianbing,MENG Chiahsiang.Automatic data segmentation for geometric feature extraction from unorganized 3-D coordinate points[J].IEEE Transactions on Robotics and Automation,2001,17(3):268-279.
[4] 刘胜兰,周儒荣,张丽艳.三角网格模型的特征线提取[J].计算机辅助设计与图形学学报,2003,15(4):444-448.
[5] 胡鑫,习俊通,金烨.基于图像法的点云数据边界自动提取[J].上海交通大学学报,2002,36(8):1118-1120.
[6] YANG M,LEE E.Segmentation of measured point data using a parametric quadric surface approximation[J].Computer-VIS 2002.IEEE Aided Design,1999,31(7):449-457.
[7] 朱心雄.自由曲线曲面造型技术[M].北京:科学出版社:2000:28-31.
[8] 张丽艳.逆向工程中模型重建关键技术研究[D].南京:南京航空航天大学机电学院,2001.

