基于蚁群算法的属性约简方法

朱元凯，陈 涛，陈 亮

(1.泰山职业技术学院信息工程系，山东泰安 271000;2.泰山学院数学与系统科学学院，山东泰安 271021)

粗糙集理论是分析不完整、不精确甚至是不一致信息系统的有力工具.知识约简是粗糙集理论研究中的核心问题，现在已经证明了粗糙集寻找最小属性集是一个NP难问题，这是由属性组合爆炸问题造成的.近年来，由意大利学者Dorie M等提出来的蚁群系统(Ant System)与蚁群算法(Ant Colony Algorithm)，是一种通用的启发式算法，主要模拟自然界蚂蚁觅食，通过在路径上信息素的传递，最终发现一条最短路径的过程.它的主要特征是采用正反馈机制、具有较强的鲁棒性和适于并行处理.本文结合粗糙集相对核的概念和蚁群算法提出了一种新的属性约简方法，既能充分利用蚁群算法的并行优化处理能力，也能解决初期信息素匮乏造成的速度慢的问题.

1 属性两两间的依赖度

属性的重要性的定义及形式为:令Ø⊂X⊆U，Ø⊂Y⊆U，U/Y≠δ={U}，给定x∈X在X中的重要性为

当X只有一个元素x时，x在X中重要性(相对于Y)为

由于|SX(Y)|/|U|就是Y关于X的支持度，记为sptx(Y).可得结论:sptx(Y)越高，X相对于Y也就越重要，X也就越有可能属于核.

2 有向图的构造

根据1中的属性间的依赖关系确定有向图中各结点间的连接关系，其中一个结点对应一个属性.构造步骤如下:

(1)选取第一个结点j={i|max(sigX(i))且min(sigi(x))，x∈A(所有的属性)};

(2)作两条有向边＜j，i1＞和＜j，i2＞，i1和i2={i|min(sigX(i))，x∈A(所有的属性)};

(3)选取下一个结点j={i|max(sigX(i))∧min(sigi(x))，x∈A'

(未被选过的点或属性)};

(4)作两条有向边＜j，i1＞，＜j，i2＞，i1，i2={i|min(sigX(i))∧x的入度≤b，x∈A(未被选过的点)}.

其中，b为预先设定的量大入度数;

(5)重复(3)和(4)，直到所有的结点都已经选取;

(6)做起始结点s，选取入度小于2(或相对其它所有属性依赖度较低的)结点k，作有向边＜s，k＞，如此作两条边;

(7)做终点e，选取出度小于2(或其它所有属性与之相对依赖度较低的)结点作k，作有向边＜k，e＞，如此作两条边.

3 有向图的各结点的信息量初始值

在以上构造的有向图中选取任意一个中间结点Ⅰ，其信息量的初值=n1+n2，

其中: n1=|{j|sigx(I)＞a，a为预先设定的最小依赖度}|，n2=|{j|sigI(x)＜b，b为预先设定的最大依赖度}|，

其它结点的信息量初值类似计算.

4 确定目标函数

根据最小约简的要求，约简的性能主要取决于两个方面:所含条件属性的个数和决策属性对其依赖度.对某一属性子集，其含属性个数越少，决策属性对其依赖度越大，则最有可能成为最小约简［2］.

构造目标函数如下:

5 算法描述

(1)设定蚂蚁的总数为m，循环次数为t，各结点的信息量(激素)浓度由3中的方法确定，△τij=0，全部蚂蚁放入结点S，pathk={蚂蚁k经过的结点}.

(2)取新蚂蚁k，path=Ø.

(3)计算蚂蚁k从当前结点i转移到下一结点j，概率如公式计算，如果概率相同时选择一个信息量最大的结点.

其中:ηij=1/dij为路径＜i，j＞的可见度:α和β分别表征信息素的迹和路线可见度的相对重要程度，α，β≥0，经过实验α、β在区间［1，5］［5］取值效果较好.

(4)把j存入pathk，如果所有属性全部选取或已经达到结点e，转下一步;否则转(3).

(5)计算目标函数，如果较前次的好，则记录下来.

(7)如果所有蚂蚁路径已经相同，则输出路径后结束;否则转(2).

6 实例应用

在信息系统中属性算法的研究中，选取典型的一组数据组成IS信息系统(如表1)，分别应用经典的属性约简算法、基于蚁群算法的属性约简算法，实验过程结果如下:

表1 信息系统IS

对表1采用属性约简的定义算法计算方法处理，得到表1的核Core(IS)={b}和一个约简RED= {a，b}.实验2使用基于蚁群算法的属性约简算法计算信息系统的核和约简集.实验3增加属性，再使用基于蚁群算法的属性约简算法计算信息系统的核和约简集.

实例分析:(1)实验1与实验2的结果约简核和约简集一致，经过对新增属性的信息系统采用以上两种算法计算(即实验3)，约简核和约简集仍一致.(2)实验2所用时间实验有明显提高，实验3所用时间(即增加属性后)比实验2增加不明显.

7 实验分析

为了测试基于蚁群算法的属性约简算法的性能，选择典型的测试函数对基于蚁群算法的属性约简算法、属性基本定义算法和基于遗传算法属性约简算法的进行测试.

三种算法参数设置相同:属性共200个，表共20个，每表记录数平均为1万条.各测试函数变量维数为50，三种算法中的局部迭代次数为100，全局迭代次数为5000.当精度达到0.0001时，算法将停止迭代。测试结果如表2:

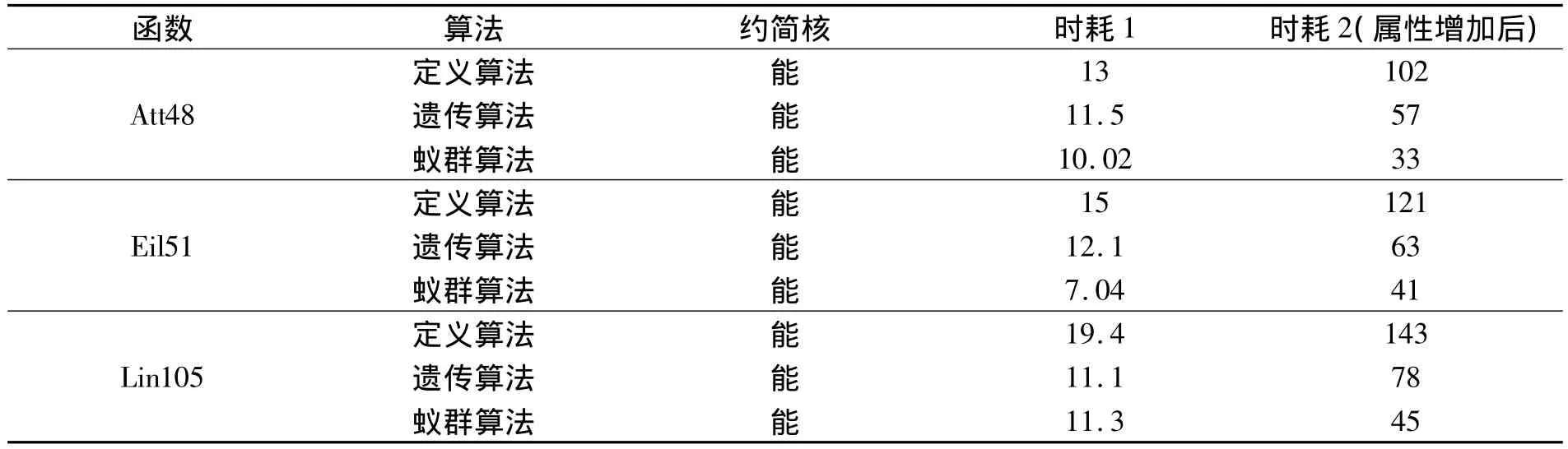
表2 三种算法的实验对比表

由表2可知，三种算法能得到属性的约简核，即都是有效的.由表2可知，基于蚁群算法的属性约简算法在求解速度都明显优于其他几种算法，在性能上有一定改善，即实验结果证明本文的算法在求解属性约简集时效率较高.当增加2倍属性规模，再进行实验。从表1的数据易知，随着属性规模扩大，其它两种算法的时耗增长迅速，搜索全局最优成功率有所下降，而本文算法的时耗较低，说明其具有较高可行性.

图1 三种算法针对Eil51的平均收敛速度曲线

图1是三种算法针对Eil51经过50次测试取得约简核的平均收敛速度曲线.从图1易知，基于蚁群算法的属性约简算法收敛速度就明显优于另两种算法.这是因为本文算法总选择较好的候选集进行计算，使算法从开始阶段的收敛速度就有明显的提高，以致间接减少了后继的处理计算量，较大提高了算法的收敛速度.

由上分析可知，基于蚁群算法的属性约简算法计算属性约简核和约简集是有效的、可行的，并且具有较高效率，收敛速度优于其它相关算法.

8 结束语

由上面的论述可知，粗糙集属性约简的算法在求最小属性约简理论上和实际应用中都是可行的，具有推广应用价值.本文受蚁群的启发，通过将条件属性集映射到一有向图，提出了用蚁群算法求解该问题，并通过实验验证了该算法的有效性.但对于该算法还存在需要研究和加以改进的地方，如有向图的初始权值的确定和计算等问题.

［1］张修文，吴伟志，等.粗糙集理论与方法［M］.北京:高等教育出版社，2003.

［2］陶志，等.基于遗传算法的粗糙集知识约简方法［J］.系统工程，2003，(2):34－36.

［3］贾修一，于绍越，等.基于Rough集和蚁群算法的属性约简方法［J］.软件学报，2006，(12):142－144.

［4］栾矗琛，盛建伦.基于粒子群算法的混洗蛙跳算法［J］.计算机与现代化，2009，(11):39－42.

［5］王俊峰，陆伟峰，朱庆保.知识约简的多族蚁群算法［J］.金陵科技学院学报，2005，(3):67－69.