分子动力学模拟乙醇/水二元混合物的扩散性质

张翠娟，程岳山

(1.泰山学院材料与化学工程系，山东泰安 271021;2.泰山医学院化学与化学工程学院，山东泰安 271016)

醇水混合物的结构性质和扩散性质在传质的理论研究和工业应用方面有重要意义.醇溶解于水时与水形成氢键，使二元混合物的性质更加复杂.醇水混合物的性质和相应纯物质的性质完全不同［1］.目前，醇的水溶液被广泛研究，尽管如此，醇的水溶液的物理化学性质仍没有彻底的解释清楚［2］.

分子动力学模拟可以研究和预测溶液中的自扩散系数，但相互扩散系数的分子动力学报道很少.计算自扩散系数时可以对每个粒子统计平均，而在计算相互扩散系数时则无法这样处理，造成相互扩散系数的不确定性较大.目前混合物的扩散系数的研究一般选取简单气体混合物为研究对象［3］.

为正确描述流体的性质，分子间相互作用模型的选取十分重要.Jorgensen［4］开发的OPLS模型已经被用于液体醇的热力学性质.最近，Wenisnk等［5］模拟了醇水混合物的动力学性质，研究中醇采用OPLS模型，水采用TIP4P模型，但作者并没有研究混合物的性质.本文在全浓度范围内对乙醇/水二元混合物的扩散性质特别是相互扩散做了研究.

1 模拟的实现

1.1 势能模型

在模拟中，水采用TIP4P模型［6-7］，该模型比较成熟而且应用广泛.乙醇分子被认为是刚性结构，有四个相互作用点，即甲基、亚甲基、氧原子和氢原子.在乙醇的分子模型中CH3-CH2-O和CH2-O-H的键角分别是108°和108.5°.相关的键长见表1.这种简化的点-点硬球模型最初由Gotlib［8］所采用.

用Lennard-Jones势来描述不同分子的不同点位之间的相互作用，用库仑函数描述长程静电作用，势能函数形式如下，

Lennard-Jones势能和电量参数［8］数值见表2.与OPLS的标准混合规则不同的是，这里不同点位和原子间的相互作用参数采用L-B混合规则.

表2 乙醇和水的Lennard-Jones分子间作用参数和库仑电量

乙醇和水的自扩散系数用两种方法计算得到:Green-Kubo法(速度自相关函数，VACF)和Einstein方法(均方位移，MSD)［9-10］，

式中vi(t)是分子i在t时刻的质心速度，ri(t)是分子i在t时刻的质心位置.乙醇/水混合物的相互扩散系数可通过计算得到［9，11］

式中D0ij是动力学相互扩散系数，C(t)是相对速度自相关函数(RVCF)，后者被定义为

Jij(t)是一个集体动力学变量，Q是热力学因子.它们可以用下面的公式计算，

上面的公式中ci是分子i的数密度，Ni是i的分子数目.γi是组分i的活度系数，xi是组分i的摩尔分数.

1.2 模拟方法

对乙醇/水混合物的模拟选取NVT系综，用Nosé-Hoover算法控制温度使其保持在298.15K.常压下混合物的实验密度数据［12］作为NVT模拟的初始输入.模拟的分子总数为500个.动力学模拟过程中每个分子都看作是刚性的，分子运动包含了围绕质心的平动和围绕质心的转动.

初始构型的选取为立方模拟盒中粒子随机分布，在三个方向上应用周期性边界条件.短程作用的截断半径为模拟盒子的边长的一半.时间步长为0.5fs，模拟的总步数为5105.观察模拟过程中温度和总能量的变化，系统在105步后达到动态平衡.后面的结果数据用来计算分析各种性质.

2 模拟结果与讨论

2.1 自扩散系数

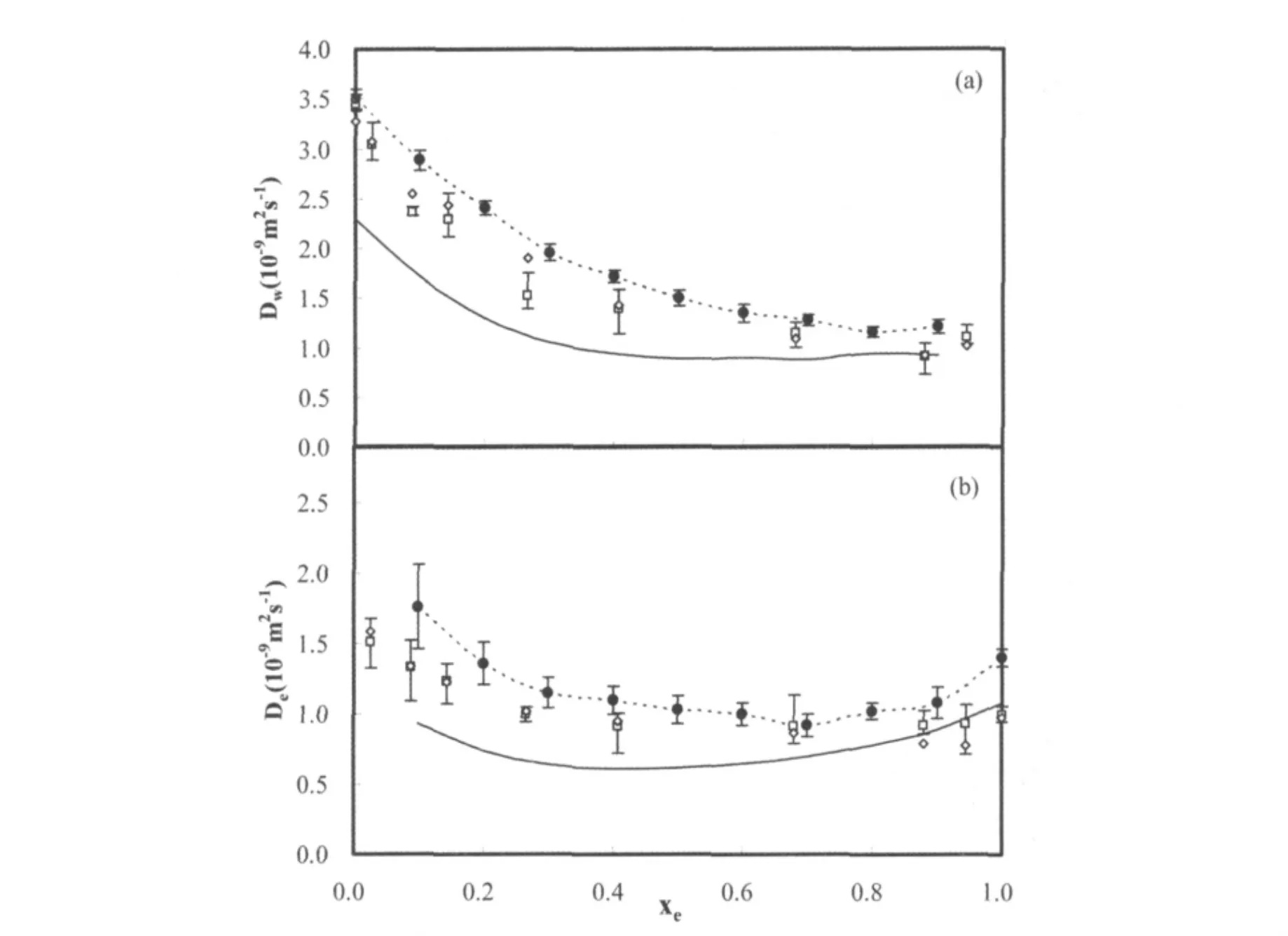
图1 (a)298.15 K时水在混合物中的自扩散系数.为清晰只画出了VACF的误差棒.□:VACF模拟值;◇:MSD模拟值;直线:实验数据［2］;虚线:文献的MD模拟值［5］.(b)298.15 K时乙醇在混合物中的自扩散系数□:VACF模拟值;◇:MSD模拟值;直线:实验数据［13］;虚线:文献的MD模拟值［5］

我们通过均方位移(MSD)和速度自相关函数(VACF)这两种方法计算得到的混合物中水的自扩散系数见图1(a).为了比较计算结果的正确性，我们同时也画出了实验数据［2］和相关的文献模拟数据［5］.可以看出，我们的计算结果比实验值大，比文献的模拟结果小.混合物中乙醇的自扩散系数见图1(b)，实验数据和相关的文献模拟数据［5］也同时画出.前面已经讨论过，使用刚性Van Leeuwen模型和OPLS模型所得到的扩散系数的不同，可能是因为采用NVT系综和NPT系综的差异造成的.从图中可以看出，混合物中水和乙醇的自扩散系数随乙醇浓度的增加，经历了一个首先降低之后趋于平缓的过程.模拟结果的这种趋势和实验值是吻合的.低乙醇浓度时，水和乙醇的自扩散系数降低说明乙醇和水存在比较强的相互作用.在高乙醇浓度时，乙醇和水的自扩散系数和混合物的浓度不相关.这种行为与乙醇分子和水分子在该浓度下的运动的强关联性相对应.在乙醇浓度较高的情况下，水分子失去了它的网状氢键结构，更易于以单个分子的形式与乙醇分子水合.

水在混合物中的自扩散行为可以用“自由水”和“结合水”来描述［13］.我们沿用Bedrov等人在文献中提出的方法［13-14］，混合物中自由水和结合水的数目可以通过分子模拟的数据分析得到.在乙醇-水的O-O径向分布函数的基础上，认为结合水是位于乙醇分子第一个配位圈之内的水分子.如果水中的氧原子和乙醇的氧原子的距离小于3.5°A，那么这个水分子就被定义为结合在这个乙醇分子上.结合水的分率就是结合水的水分子数目与全部水分子数目的比值.我们计算出该比值随乙醇浓度的变化，见图2.从图中可以看出，结合水的摩尔分率随着乙醇浓度的增加而增大.在乙醇浓度很高的情况下，绝大多数水分子以结合的形式存在，此时水的自扩散系数与乙醇的关联性较大.

图2 乙醇/水混合物中由动力学模拟计算得到的束缚水分子的比例

根据上面的分析，水在乙醇-水溶液中的自扩散行为可以表示为两种扩散行为的贡献:自由水的贡献和结合水的贡献［13-14］.这里Dw

0是纯水的自扩散系数，De是混合物中乙醇的自扩散系数.Xb是我们计算得到的结合水的摩尔分率.Kb为结合系数.关联动力学模拟计算得到的自扩散系数(为了保持图形清晰，只画出MSD的结果)和方程8，我们取Kb的最优值为1.24.从图3中可以看出，方程(8)合理地描述了乙醇-水混合物中体系中水的自扩散系数随乙醇浓度的变化.

图3 方程(8)拟合得到的水的自扩散系数随乙醇浓度的变化

2.2 相互扩散系数

为了得到混合物的相互扩散系数，我们根据方程(5)计算了相对速度自相关函数C(t).混合物的RVCF的震荡明显比VACF大的多.与VACF相比［11］，RVCF是一个集体变量并且波动较大，由此根据RVCF计算得到的相互扩散系数(Dwe)与自扩散系数相比，精度较低.一个典型的相对速度自相关函数的积分随着最大上限积分时间(tmax)的变化见图4.在图中可以看出，积分值在10 ps以后趋于稳定，因此我们舍弃10 ps以内的数据，采用的积分值为10到75ps的平均值.

为了得到合理的数据，本文中所有的相互扩散系数都由上述类似程序处理得到.热力学因子Q可以由不同浓度组成时的化学势得到.Q可以根据Kirkwood-Buff的理论［15］由分子模拟计算得到，但获得一个好的统计结果有一定难度［16］.我们采用的热力学因子的数值是从乙醇-水溶液的汽液相平衡数据计算得到的［17］.全浓度范围下乙醇-水混合物的相互扩散系数见图5，实验数据［18］也在图中画出.到目前为止，因为在计算集体性质时存在固有的统计性较差的现象，真实混合物中相互扩散系数的分子动力学研究报道很少.然而，本文中所得到的乙醇-水的相互扩散系数的结果与实验值相比是令人满意的.

3 结论

本文采用分子动力学的方法研究乙醇/水混合物的扩散性质.模拟中乙醇分子采用点点刚性模型，水分子采用TIP4P模型.比较不同浓度时乙醇和水的自扩散系数分别与实验值和文献的MD模拟值，我们的模拟结果比实验值稍大.混合物中自扩散系数和混合物的结构有关.水溶液中，水的自扩散系数描述为结合水分子和自由水分子的综合贡献.MD模拟得到的乙醇/水混合物相互扩散系数与实验值十分吻合.计算结果表明，我们采用的乙醇和水的模型对正确描述乙醇/水混合物的结构性质和扩散性质是可行的.

［1］Guàrdia E，MartíJ，PadróJA，etal.Dynamics in Hydrogen Bonded Liquids:Water and Alcohols［J］.JMol Liq，2002，(96-97):3 -17.

［2］Price W S，Ide H，Arata Y.Solution Dynamics in Aqueous Monohydric Alcohol Systems［J］.JPhys Chem A，2003，(107):4784-4789.

［3］Zhou J，Lu X H，Wang Y R，et al.A Molecular Dynamics Simulation of Infinite Dilute Diffution Coefficients of Benzene and Naphthalene in Supercritical Carbon Dioxide［J］.Chem Jof Chinese Universities，2000，(21):762-765.

［4］Jorgensen W L.Optimized Intermolecular Potential Functions Liquid Alcohols［J］.JPhys Chem，1986，(90):1276-1284.

［5］Wenisnk E JW，Hoffmann A C，Maaren P J，etal.Dynamic Properties ofWater/ElcoholMixtures by Computer Simulation［J］.JChem Phys，2003，(119):7308-7317.

［6］Jorgensen W L，Chandrasekhar J，Madura JD，etal.Comparison of Simple Potential Functions for Simulating Liquid Water［J］.JChem Phys，1983，(79):926-935.

［7］Chialvo A A，Cummings P T.Microstructure of Ambient and SupercriticalWater.Direct Comparison between Simulation and Neutron Scattering［J］.JPhys Chem，1996，(100):1309-1316.

［8］Gotlib IY，Piotrovskaya EM.Properties of Coexisting Phases for the Ethanol-Ethane Binary System by Computer Simulation［J］.J Phys Chem B，1999，(103):7681-7686.

［9］Stoker JM，Rowley R L.Molecular Dynamics Simulation of Real-Fluid Mutual Diffusion Coefficientswith the Lennard-Jones Potential Model［J］.JChem Phys，1989，(91):3670-3676.

［10］Zhou Y，Miller G H.Green-Kubo Formulas for Mutual Diffusion Coefficients in Multicomponent Systems［J］.JPhys Chem，1996，(100):5516-5524.

［11］Kamala CR，Ayappa K G，Yashonath S.Mutual Diffusion in A Binary Ar-Kr Mixture Confined within Zeolite NaY［J］.Phys Rev E，2002，(65):1-12.

［12］Easteal A J，Woolf L A.Pressure and Temperature Dependence of Tracer Diffusion Coefficients ofMethanol，Ethanol，Acetonitrile，and Formamide in Water［J］.JPhys Chem，1985，(89):1066-1069.

［13］Bedrov D，Borodin O，Smith GD.Molecular Dynamics Simulation of1，2-DimethoxyethaneWater Solutions.2.Dynamical Properties［J］.JPhys Chem B，1998，(102):9565-9570.

［14］Borodin O，Bedrov D，Smith GD.Concentration Dependence ofWater Dynamics in Poly(Ethylene Oxide)Water Solutions from Molecular Dynamics Simulations［J］.JPhys Chem B，2002，(106):5194-5199.

［15］Kato T.Determination of Velocity Correlation Coefficients in Aqueous Solutions of2-butoxyethanol by Quasi-elastic Light Scattering，Pulsed-gradient FT-NMR，and Rayleigh-Brillouin Scattering［J］.JPhys Chem，1985，(89):5750-5755.

［16］Kataoka Y.The Concentration Fluctuations and the Mutual Diffusion Coefficient in the Supercritical Solution［J］.JMol Liq，2001，(90):35-43.

［17］Yang X N，Wang R S.Correlation and Prediction of Liquid Diffusion Coefficients in Binary Systems［J］.Chinese J of Chem Eng，1996，(4):104-111.

［18］Tyn M T，CalusW F.Temperature and Concentration Dependence of Diffusion Coefficients of Some Binary Liquid Systems［J］.JChem Eng Data，1975，(20):310-316.