非理想网络环境下线性控制系统的稳定性分析

孔宪明，鞠培军，马晓燕，张 卫，刘国彩，房 亮

(泰山学院数学与系统科学学院，山东泰安 271021)

近年来，网络控制系统(NCS)的分析和设计问题引起了许多学者的广泛研究.与通常的控制系统相比，NCS具有低成本、易于信息共享、易于维护和灵活性大等优点.但是，由于控制系统通过网络进行连接，不同节点的实际距离可能非常远，并且由于网络的不可靠性以及未知干扰因素的影响，数据包在网络中传输会不可避免的遇到时间延迟、丢包以及错序等情况(称为非理想网络状况)，这些情况都会导致系统的性能下降甚至不稳定.目前，对于NCS的研究，大都是在理想网络环境下讨论的，或仅研究网络时延和丢包［1－3］，或仅研究信息受限等［4－6］，对于一般的非理想网络环境下NCS的研究还不多见［7］.

本文将针对一类非理想网络环境下线性控制系统，建立一种区间时滞系统模型，研究其稳定性分析问题，通过构造一个新的Lyapunov－Krasovskii泛函，从而得到一个更少保守性的稳定性判据.这种方法很容易推广到反馈控制和H无穷控制的设计中.

1 问题描述

考虑控制系统状态方程

其中，x(t)∈ℝn和u(t)∈ℝm分别是系统状态和系统控制输入，A和B0是具有恰当维数的常数矩阵.假设(A，B0)是可控的.系统通过网络渠道连接，网络控制系统结构如图1.

假定系统采样器是时针驱动，而零阶保持器是事件驱动，采样周期是一个正整数T.假设所有的状态是可测的，数据传输是经过单包传输.其中，采样序数是Si(i=1，2，3，…，∞)，而零阶保持器的接受序数为tk(k=1，2，3，…，∞).采样值通过网络渠道传输，且成功传输的信息将存放在缓存器中.缓存器的输出信息为¯x(tk)，依据此信息可设计控制器.

图1 网络控制系统结构图

假设网络控制系统传输时滞为τSCk，数据传输中的丢包数为d(k)，则可得到¯x(tk)=x(tk－τSCk)，其中，tk=Si+τSCk，tk+1=Sj+τSCk+1(i，j∈(1，2，3，…，∞)).显然，∪∞k=0［tk，tk+1)=［t0，∞)，t0＞0.在实际控制中倾向于采用那些新的信息，而把旧的数据包放弃.所以假设Sj＞Si(i，j∈(1，2，3，…，∞))，同时考虑到零阶保持器的作用，可得

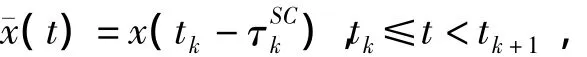
令τ(t)=t－tk+τSCk，则τ(t)是分段线性函数，且t≠tk时，˙τ(t)=1.采取状态反馈控制u(t)= K¯x(t)，其中，K为状态反馈阵，则系统(1)可写为

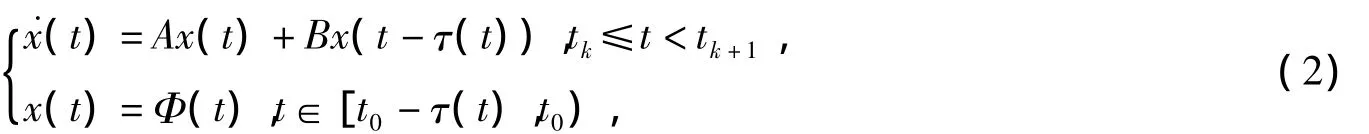
其中Φ(t)为系统(2)的初始条件，B=B0K，变时滞τ(t)满足

至此，我们建立了一种非理想网络环境下线性控制系统的区间时滞系统模型.下面将进行稳定性分析.首先给出如下引理，它将在主要结果的证明中起着重要作用.

引理1［8］对任意矩阵W∈ℝn×n，W=WT＞0和一个标量γ＞0，向量函数˙x∶［－γ，0］→ℝn使得下列不等式成立

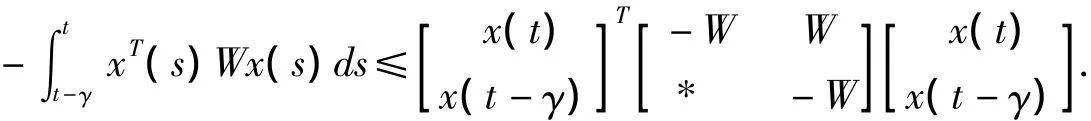
2 稳定性新判据

定理1 对于满足条件(3)的系统(2)，如果存在矩阵P＞0，S1＞0，S2＞0，S3＞0，S4＞0和Q=，满足下面的矩阵不等式(LMI)，则系统(2)是渐近稳定的.

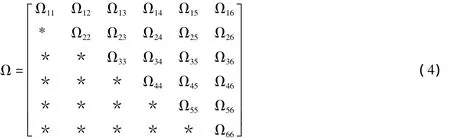
证明:构造Lyapunov－Krasovskii泛函

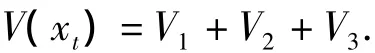
对V(xt)沿(2)求导得

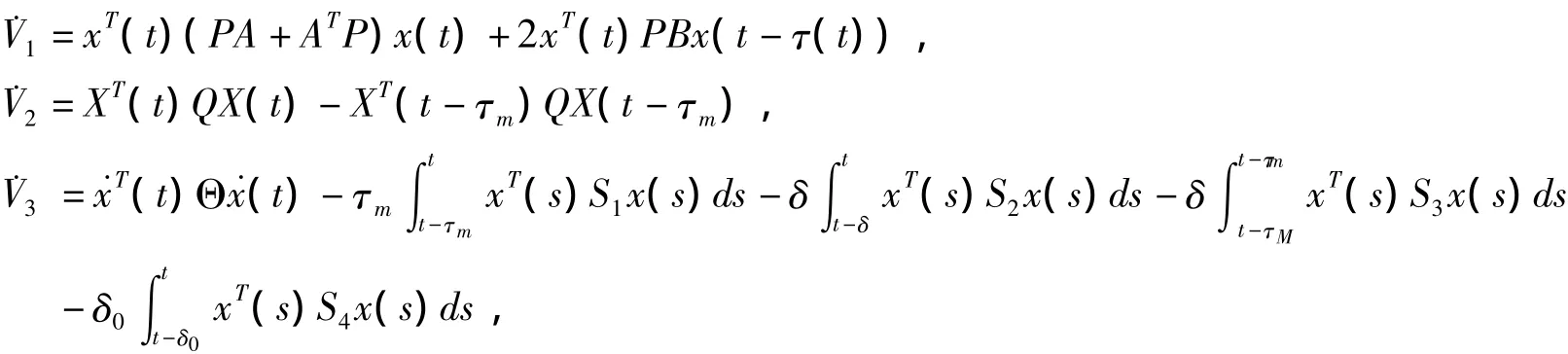
由引理1得

~A=［A B 0 0 0 0］.由上得 ˙V≤ξT(t)Ωξ(t).若LMI(4)有解，则 ˙V≤－λξT(t)ξ(t)≤－λxT(t)x(t)，其中λ=λmin(－Ω)＞0.从而由Lyapunov－Krasokii稳定性定理知，满足条件(3)的系统(2)是渐近稳定的.

3 数值算例

为了验证所提出方法的优越性，假设网络控制系统已转化为系统(2)，其中

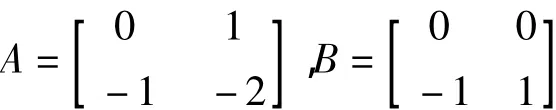
当时滞导数信息未知时，利用定理1及MATLAB软件中的LMI工具箱，可得到表1.从表格中看到，应用本文方法极大减少了结果的保守性.

表1 保证系统稳定的时滞区间

4 结论

本文针对一类非理想网络环境下的线性控制系统，建立了一个区间时滞线性系统模型，通过构造一个新的Lyapunov－Krasovskii泛函，讨论了系统的渐近稳定性问题，得到了一个基于LMI的稳定性判据.数值算例说明所得结论具有较小的保守性.

［1］郭戈，贾二娜.网络化控制系统中的延时问题:分析与展望［J］.控制与决策，2009，24(1):1－6.

［2］孙海燕，侯朝桢.具有数据包丢及多包传输的网络控制系统稳定性［J］.控制与决策，2005，20(5):511－515.

［3］岳东，彭晨，Han Qing－Long.网络控制系统的分析与综合［M］.北京:科学出版社，2007.

［4］Liberzon D.On stabilization of linear systemswith limited information［J］.IEEE Trans on Automatic Control，2003，48(2):304－307.

［5］Liberzon D.Quantization，time delay and nonlinear stabilization［J］.IEEE Trans on Automatic Control，2006，51(7):1190－1195.

［6］Fu M Y，Xie L H.The sector bound approach to quantized feedback control［J］.IEEE Trans on Automatic Control，2005，46(11): 1698－1711.

［7］彭晨，田恩刚.一种改进的具有非理想网络状况的网络控制系统分析与综合方法［J］.自动化学报，2010，36(1):188－192.