标准正态分布在积分中的应用

陈志成，张红云

(河南科技学院数学系，河南新乡 453003)

1 引言

被积函数为指数函数且原函数不是初等函数的积分问题历来是积分的难点，它困扰着学习者和工作者.尽管可以部分题目采用极坐标变换，但是计算过程往往比较繁琐.本文利用标准正态分布的密度函数及性质较系统的解决了该类问题的积分，并对该问题分类给出了相应的积分公式便于记忆和掌握.

2 几个重要结论

定理1［1－2］若a＞0，则

推论［3］对任意k＞0，则

定理2 若a＞0，x1＜x2，则

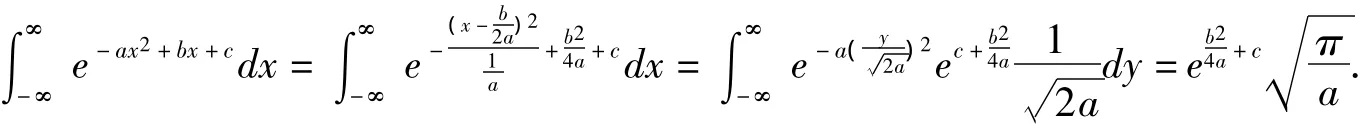
定理4 若a＞0，b，c为实数且x1＜x2，则

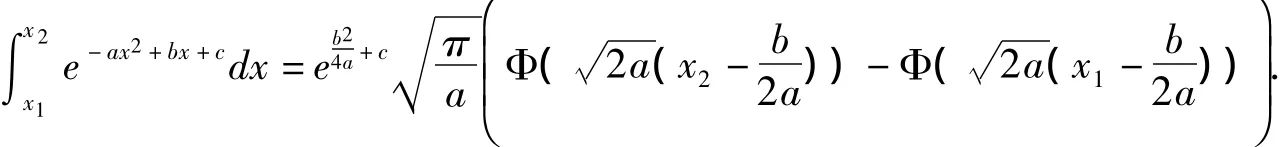
证明:由于被积函数xe－ax2是奇函数且积分区间对称，则

其中Y服从标准正态分布N(0，1)，因而σ2=1，σ2=E(Y2)－(E(Y))2，E(Y)=0，E(Y2)=1.易证

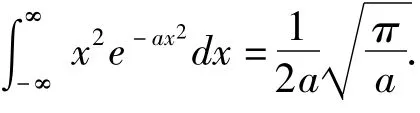
注:本定理通过利用标准正态的相关性质和结论求解，计算过程简单，思路清晰;相比较而言若利用经常采用的极坐标变换x=r sinθ，y=r cosθ进行求解，需要把一重积分转化为二重积分，求解过程比较复杂［4］.

定理7 当a＞0，－∞＜k＜∞时，则

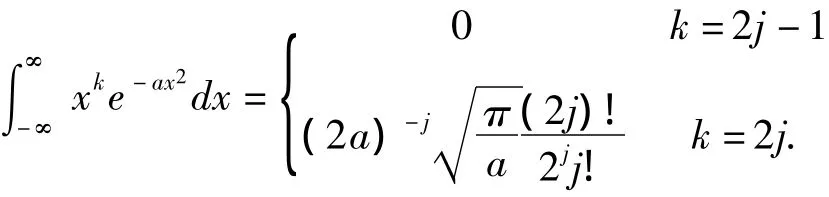
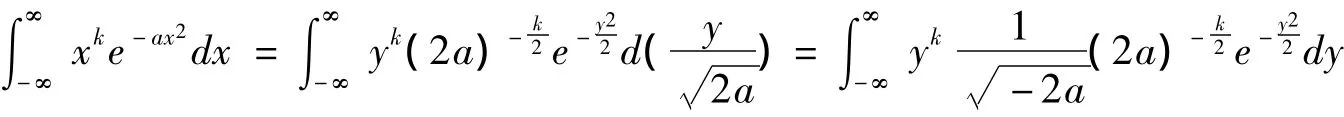
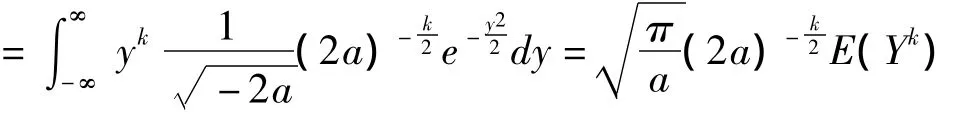
(1)当k是奇数时，显然E(Yk)=0;

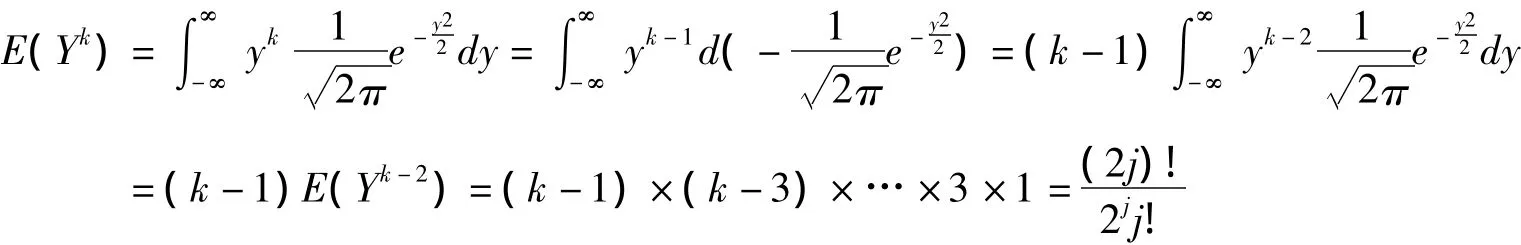
则

［1］盛骤，谢式千，潘乘毅.概率论与数理统计［M］.北京:高等教育出版社，2010.

［2］邓集贤，杨维权，司徒荣，邓永录.概率论及数理统计［M］.北京:高等教育出版社，1988.

［3］李贤平.概率论基础［M］.北京:高等教育出版社，1997.

［4］孙荣恒.应用概率论［M］.北京:科学出版社，1998.