遗传算法整定PID控制器在下肢电刺激康复训练中的应用

郭新奇 李 晴 郝林琳

1 引言

20世纪60年代，Liberson首次利用电刺激腓神经成功地矫正了偏瘫患者足下垂的步态，开创了功能性电刺激（functional electrical stimulation，FES）用于运动和感觉功能康复治疗的新途径[1]。研究表明，FES通过电流脉冲序列来刺激肢体运动肌群及其外周神经，能够有效地恢复或重建截瘫患者的部分运动功能，是重要的康复治疗手段[2]。

如何精密控制FES的脉冲电流强度和触发时序以保证电刺激作用效果能准确完成预定的功能动作是FES的技术关键。早期的FES系统采用开环控制，凭经验预先设置刺激强度和触发时序[2-5]，缺乏反馈机制。但由于肌肉、神经组织生理特性对刺激响应的随时变化以及受试者之间的个体差异，开环控制的FES系统准确性和稳定性比较差。Lan等[6]将反馈机制引入功能性神经刺激中弥补了开环系统的不足。根据作用效果与预定动作偏差，用闭环控制来自动调整FES刺激强度和时序参数，明显提高了FES系统的准确性和稳定性[7-10]。闭环控制需采用适当的反馈调节算法，比例微积分(proportional integral differential, PID)是一种非常实用的反馈调节算法，它根据系统检测或操作偏差，利用比例、积分、微分运算获得所需调节量以对系统进行反馈控制，因其操作方便而广泛用于工程实践。尤其当被控系统特性参数不明确或难以及时在线测定时，稳妥的闭环控制即可采用PID整定算法。面对肌肉的复杂性和时变性操作环境，由于PID的稳定性好、工作可靠，目前仍在功能性电刺激领域得到了广泛的应用[11-12]。PID核心技术是精密确定其中比例、积分、微分系数，尤其在FES领域，对系统稳定性要求极为严格，所以对PID系数选择尤为重要。PID控制要取得较好的控制效果，必须调整好比例、积分和微分三种控制作用，形成控制量中既相互配合又相互制约的关系。传统的系数整定过程主要依赖于工程经验，直接在控制系统的试验中进行系数调试，主要有临界比例法、反应曲线法和衰减法。临界比例法，又称Ziegler-Nichols整定法[13-14]，最为常用。然而这些方法在某种程度上都没有脱离人为的凑试，为了提高控制效率，出现了通过多种方法来确定PID系数的方法。例如Visioli等[15]用模糊自适应算法来选择PID系数，Benaskeur等[16]利用逆推法对PID系数进行确定。

利用遗传算法（genetic algorithm, GA）对PID的比例、积分和微分系数进行整定，是一种通过模拟自然进化过程搜索最优解的方法。从代表问题可能潜在的解集的一个种群开始，每一个种群则由经过编码的一定数目的个体组成[17]。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和突变，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。由于遗传算法对潜在的解决方案直接搜索，对适应函数基本无限制，因此，选用遗传算法对PID控制器的三个系数进行确定，优化高效的组合是一个很好的选择。

2 PID算法及其遗传算法整定

2.1 PID原理

PID由比例单元P、积分单元I和微分单元D三部分组成，根据系统的误差，通过设定的Kp、Ki和Kd三个系数对系统进行控制[18]。

其中Kp是比例系数，Ki是积分系数，Kd是微分系数，error为预设输出与实际输出的偏差，u(t)为PID的输出，同时又是受控系统的输入。

2.2 Ziegler-Nichols整定方法

Ziegler-Nichols方法的整定思想是基于系统稳定性分析。该整定算法首先设Ki=0，Kd=0，然后增加Kp直至闭环系统开始出现振荡（即系统极点出现在虚轴上），记下此时Kp值（表示为），然后运用如下整定公式：

2.3 基于遗传算法整定的PID控制器

在遗传算法整定PID控制器系数的过程中，采用二进制编码方式，用二进制编码串来分别表示PID控制器比例，积分和微分系数三个决策变量。遗传算法流程图如图1所示。

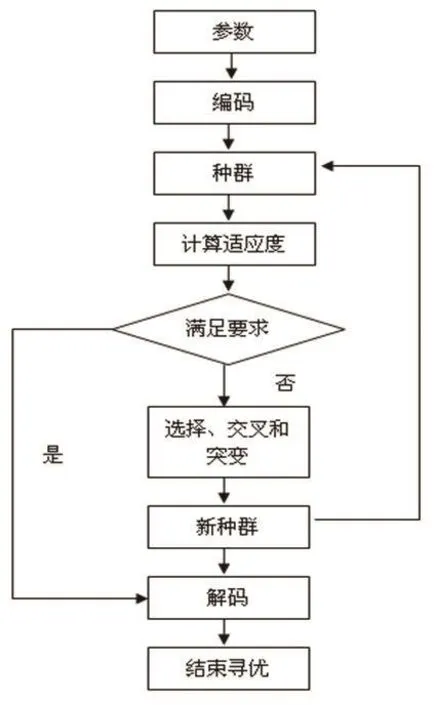
图1 遗传算法流程图

首先确定参数整定的范围，这个范围由用户给定，根据精度的要求进行编码，选取二进制串表示每一个参数，并建立参数间的关系再把二进制串连起来组成一个长的二进制字串，该二进制字串则为操作对象。选取初始种群，由系统的复杂程度来确定种群的大小，根据待搜索的特征维数总量随机产生一系列的由二进制位组成的个体。由‘01’序列的组合构成每一个个体，针对每一个个体，依据制定的规则，构建适合度函数并且计算其适合度作为评价个体适合度的依据，通过选择算子，交叉算子，与突变算子产生下一代个体。

选择算子用来根据个体的适合度选取较好的个体，通过繁殖产生下一代个体，体现了适者生存，不适应者淘汰的自然法则。给出目标函数f(bi)计算个体bi的适应度。适应度较高的个体，繁殖下一代的数目较多；适应度较小的个体，繁殖下一代的数目较少，甚至被淘汰。这样，就产生了对环境适应能力较强的后代。对于问题求解角度来讲，就是选择出和最优解较接近的中间解。交叉算子对于选中用于繁殖下一代的个体，随机地选择两个个体的相同位置，按交叉概率Pc在选中的位置实行交换。这个过程反映了随机信息交换；目的在于产生新的基因组合，也即产生新的个体。突变算子以变异概率Pm对某些个体的某些位执行变异。在突变时，对执行变异串的对应位求反，即把1变为0，把0变为1。变异概率Pm与生物变异极小的情况一致，所以Pm的取值较小，一般取0.01～0.20。通过以上三个算子产生新一代的个体后，重复以上运算，当最优个体的适应度达到给定的阀值，或者最优个体的适应度和群体适应度不再上升时，则算法的迭代过程收敛、算法结束。否则，用经过选择、交叉、变异所得到的新一代群体取代上一代群体，并返回继续循环执行。

3 FES实验设置

本实验利用Labview实现遗传算法对PID系数的优化，借助膝关节角度测量器获得的信息进行 PID算法反馈控制，以此来调整功能性电刺激助行系统脉冲电流幅值的大小，改变刺激强度，使膝关节完成预设的角度动作。本实验中采用的刺激系统包含微处理器和刺激脉冲发生电路，含6条刺激通道，电池供电。我们根据实验需要对该助行装置进行了改进，电刺激脉冲序列采用经典的Lilly波形，脉冲频率为30 Hz、脉宽100 µs，电流脉冲的幅值在0～150 mA范围内可调。本实验通过同仁医院伦理委员会批准，对6名受试者（3名男性，3名女性）进行下肢功能性电刺激双侧股四头肌表面电刺激实验。受试者身体健康，无下肢肌肉、骨骼疾患，无神经疾患及严重心肺疾患。其平静坐于测试台上，将表面刺激电极固定于股四头肌的两端位置，未施加电刺激时小腿放松、保持垂直悬空状态（定义此时为初始角度0o）。实验数据采样率为256 Hz，数据记录时长为60 s。实验前需预先设定好期望的膝关节角度运动轨迹，利用电子角度测量器实时记录膝关节张角变化，并且将其作为反馈信号通过AD转换引入Labview算法程序。实验前分别利用Ziegler-Nichols和遗传算法对PID在系数进行整定，其中遗传算法选用的个体种群数为50，进化的代数确定为100，交叉算子概率为0.6，突变概率的确定采用自适应的方法，与个体的适合度有关，越高的适合度，则突变概率越低。在整定优化的PID系数的作用下，计算求得刺激脉冲强度的大小，来控制功能性电刺激装置刺激相应得肌肉，使得膝关节角度能够按照预设轨迹进行运动，直至完成要求的整套动作。

4 结果与讨论

分别利用传统的Ziegler-Nichols PID整定算法和GA-PID整定算法优化的PID系数对6名受试者实验过程中FES电流脉冲幅值进行在线调制，使得膝关节角度的运动轨迹在FES控制下与预设运动轨迹相吻合。对6名受试者进行刺激实验的结果均表明，基于GA整定的PID控制器优于传统的Ziegler-Nichols PID控制器，本文列其中一名受试者刺激实验对控制结果予以说明（见图2，图3）。

图2 Ziegler-Nichols整定法的PID控制结果

图3 GA整定法的PID控制结果

图2中，上图为Z-N整定PID控制器追踪预期关节角度的结果，其中实线为预期运动轨迹、虚线为实际输出关节角度；下图为Ziegler-Nichols整定PID控制器调制电流的脉冲幅值。图3中上图为GA整定PID控制器追踪预期关节角度的结果，其中实线为预期运动轨迹、虚线为实际输出关节角度。下图为GA整定PID控制器调制电流的脉冲幅值。图中实线表示预期运动轨迹、虚线为实际输出关节角度。X轴为时间，Y轴为膝关节运动角度。对比图2与图3可以看出遗传算法整定的PID新算法能更好地控制膝关节角度运动轨迹。

为更清楚地观察两种PID整定方式的控制误差，监测了控制过程中偏差的均方根（RMS）值变化（如图4所示，纵轴为RMS偏差的对数值。图中实线为Ziegler-Nichols整定控制结果，虚线为GA整定整定结果）。

图4 PID整定控制过程中偏差的均方根(RMS)值变化图中纵轴为RMS偏差的对数值；实线为Ziegler-Nichols整定结果，虚线为GA整定结果

由于GA是在解空间进行高效启发式搜索，能够在保持原有最优解的基础上，寻找更好的解决方案，使得整定的PID控制器具有更高的控制精度，误差维持在相对更低且更为稳定的范围内，相比之下Ziegler-Nichols整定法的控制误差则波动较大。另外利用遗传算法优化的PID控制器系数，通过选择算子，交叉算子和突变算子进行全局优化，避免搜索的过程陷入局部最优解，能够有效地克服控制过程中超调量的产生，大大降低超调量在控制过程中可能带来的安全隐患。

利用遗传算法PID控制器系数整定需要重视选择，交叉和突变算子概率的确定：选择算子概率过大会降低搜索解得收敛速度，过小则会发生有效基因的缺失；交叉算子概率关系到遗传算法优质基因重组和解寻优的能力，而突变算子概率过小无法保证基因的多样性和容易陷入局部最优解，过大则会破坏掉优秀的个体结构，所以在应用中需根据不同控制对象，选择合理的概率参数，使得算法能够快速，合理地得到优化的控制系数。

5 结论

将遗传算法引入FES的PID反馈控制器中，利用适者生存和优胜劣汰的原理，逐代演化对PID控制器的比例、积分和微分系数进行优化以精确对功能性电刺激的电流脉冲幅值进行在线调制，使得膝关节角度的运动轨迹在FES控制下与预设运动轨迹相吻合经过与当前主流的通过经验值或者人为的手工调试的传统PID控制器相比，基于遗传算法整定的PID算法相对于传统的Ziegler-Nichols整定PID算法具有更高的反馈控制精度和更为稳定的反馈控制特性。因此，更适合用于要求反馈控制性能严格稳定的FES系统，从而保证了更为稳定的康复训练效果。

[1]万柏坤,李佳,明东.用于肢体运动系统的神经假体研究进展[J].中国医疗器械杂志.2006,30(4):235-240.

[2]蓝宁,肖志雄,聂开宝,等.功能性电刺激原理、设计与应用[J].中国康复理论与实践,1997,4(3):151-154.

[3]Hoshimiya N, Naito A. A multichannel FES system for the restoration of motor function in high spinal cord injury patients: a respiration-controlled system form multijoint upper extremity[J]. IEEE Trans. Biomed. Eng,1989,36(7):754-760.

[4]Buckett JR, Peckham PH, Thrope GB, et al. A flexible, portable system for neuromuscular stimulation in the paralyzed upper extremity[J]. IEEE Trans Biomed Eng,1988,35(11):897-904.

[5]Hausdorff JM , Durfee WK. Open-loop position control of the knee joint using electrical stimulation of the quadriceps and hamstrings[J].Med Bio Eng Comput,1992,29(3):269-280.

[6]Lan N, Crago PE, Chizeck HJ. Control of end-point forces of a multijoint limb by functional neuromuscular stimulation[J]. IEEE Transactions on Biomedical Engineering[J].1991,38(10): 953-965.

[7]Kamnik R, Shi JQ, Murray-Smith R, et al. Nonlinear modeling of FES-supported standing-up in paraplegia for selection of feedback sensors[J]. IEEE Transaction on Neural Systems and Rehabilitation Engineering.2005,13(1):40-52.

[8]Hunt KJ,Stone B, Negaord NO,et al. Control strategies for integration of electric motor assist and functional electrical stimulation in paraplegic cycling: utility for exercise testing and mobile cycling[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering,2004,12(1):89-101.

[9]Kurosawa K, Futami R, Watanabe T, et al. Joint angle control by FES using a feedback error learning controller[J]. IEEE Trans Neural Syst Rehabil Eng,2005,13(3):359-371.

[10]Chizeck HJ, Lan N, Palmieri LS, et al. Feedback control of electrically stimulated muscle using simultaneous pulse width and stimulus period modulation[J]. Biomedical Engineering IEEE Transactions on,1991,38(12):1224 -1234.

[11]Ferrarin M, Acquisto E D, Mingrino A.“An experimental PID controller for knee movement restoration with closed loop FES system[J]. Engineering in Medicine and Biology Society,1996. Bridging Disciplines for Biomedicine. Proceedings of the 18th Annual International Conference of the IEEE,1996(1): 453-454.

[12]Y u N Y, C h e n J J, J u M S. ClosedLoop control of quadriceps/ hamstring activation for FES-induced standing up movement of paraplegics[J]. Journal of Musculoskeletal Research,2001,5(3):173-184.

[13]Basilio JC, Matos SR. Design of PI and PID controllers with transient performance specification[J]. IEEE Transactions on Education,2002,45(4):364-370.

[14]Oubrahim R, Leonard F. PID tuning by a composed structure[J]. Control '98. UKACC International Conference on (Conf.Publ.No.455).1998(2):1333-1338.

[15]Visioli A. Tuning of PID controllers with fuzzy logic[J]. Control Theory and Applications, IEE Proceedings, 2001,148(1):1-8.

[16]B e n a s k e u r A R, D e s b i e n s A. Backstepping-based adaptive PID c ontrol[J].Control T h e ory and Applications,IEE Proceedings,2002,149(1): 54-59.

[17]刘金琨.先进PID控制MATLAB仿真[M].3版.北京:电子工业出版社,2011:325-358.

[18]Cheng L,Zhang G, Wan B,et al. Radial basis function neural network-based PID model for functional electrical stimulation system control[J]. Conf Proc IEEE Eng Med Biol Soc,2009,2009:3481-3484.