基于灵敏度分析的客车骨架优化分析研究

魏 允

(河南工业职业技术学院网络管理中心,河南南阳 473009)

0.引言

汽车的三大总成中,车身结构的设计历来是汽车设计中的重中之重。车身直接决定整车的安全性、舒适性、美观以及由车身外形空气动力学性能决定的操控稳定性、动力性和经济性[1]。目前,国内客车整车制造的协调性与国外有较大差距。一方面,对设计过程中的应力和位移薄弱区域往往采用局部加强,造成车架越来越重;另一方面,对个别能够减薄、减少的构件,却因无精确的减轻数据不敢实施,造成材料的浪费。因此,对车架进行合理优化,在满足强度和刚度的前提下,实现轻量化,对节约钢材,节省能源,减少油耗,降低轮胎磨损,减轻环境污染均有积极的意义。

我们在轻量化方面通常采用的做法是:在不改变结构的前提下,通过改变型材截面的大小或形状以获得体积的减小。型材截面尺寸的改变量通常以“等强度、等刚度”为指导[2],但具体的改变量却并无准确的依据。本文以某全承载客车的轻量化为背景,通过对目标函数和状态变量的变化较敏感的参数为设计变量,以灵敏度计算结果为依据,参照模态的分析结果,实现对客车车身的轻量优化。

1.客车车身有限元模型

1.1 有限元模型

客车车身骨架是复杂的空间薄壁杆系组成的超静定结构,由型钢和异形截面管焊接组合而成。为了使有限元模型能够真实的反映工作情况,本文对杆件结构采用了纯梁结构建模;对悬架采用实体方式建模。整个车身有限元模型包括2653个节点,12320个单元。图 1所示为客车骨架的有限元模型。

1.2 载荷和边界条件

根据客车的实际承载情况,我们对有限元模型进行了约束和加载,载荷主要由以下部分组成:骨架自重,在 ANSYS中定义材料密度即可生成;乘客及行李重量,本文按超载至55人计算。每人重 100Kg(含座椅重量),每人携带 60Kg行李。乘客重量按座位的具体位置均匀加在对应梁上,行李重量则均匀分布在货箱内。另外,发动机、变速器等随车部件载荷按图纸施加至相应的节点处。

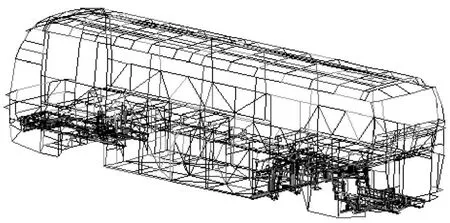
图 1 客车骨架有限元模型

汽车车身承受着来自道路及装载的各种载荷,这些随机载荷会导致汽车结构产生疲劳损坏。所以,在结构设计时,必须考虑到实际行驶中的最大变形量。长期的实践表明,极限扭转工况的变形量最大[3],试验也证实了这一点。

1.3 有限元模型的试验验证

为验证该车车身有限元模型的正确性,在参考国家客车车身应力测试标准的前提下,根据实际情况在结构上应力和位移较大的区域内布 70个测点[4],检测客车在水平弯曲工况下的应力情况。具体加载方案与有限元模型的载荷分布一致。图 2所示为对应测点的应力理论计算曲线与实测曲线。

如图 2所示,理论曲线与实测曲线变化趋势基本一致。个别测点应力有差异,其原因是由于试验时实际载荷施加不均匀导致。证明该车的有限元模型是正确的。

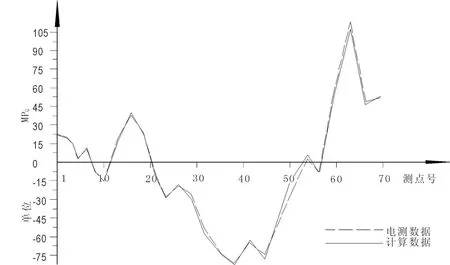
图 2 测点的电测应力与理论应力对比曲线

2.灵敏度分析及优化[5-6]

灵敏度分析是优化设计的重要一环,可成倍提高优化效率,通过灵敏度分析可以计算出结构响应值对于各设计变量的导数,以确定设计变化过程中对结构响应最敏感的部分,从而可以获得最关心的灵敏度系数和最佳的设计参数。

在对客车车身进行轻量化时,由于车身附件及内饰的装配工艺要求的局限,主要通过改变梁的截面尺寸和厚度来实现要求。

与此同时,整车的刚度和强度也随着梁尺寸的改变而剧烈变化。灵敏度分析就是选取对于车身刚度和强度变化影响最小参数作为优化设计变量,通过改变截面尺寸使其体积最小,从而实现重量减轻的目标。

2.1 目标函数的确定

轻量优化的目标是在满足应力和位移要求的前提下,质量取最轻。由于质量与体积呈线性变化 (密度均匀),因此,体积最小意味着质量最轻。目标函数定义为结构的体积最小。

2.2 状态变量的确定

状态变量是指约束设计的数值,它一般是设计变量的函数。轻量化是通过改变截面形状尺寸实现的,但绝不是以降低车架的强度与刚度来获得的。因此,将车架的应力和位移定义为状态变量,实现“等强度,等刚度”的要求。

2.3 设计变量的确定

优化的结果是通过改变设计变量实现的,在优化设计中,可设置的设计变量最大数目有限[7]。空间薄壁梁的宽、高、壁厚将占用 3个参数,所以要选取灵敏度值大的梁进行轻量化。表 1为部分参数的灵敏度分析结果。图 3、4、5、为左侧围、底架中段截面梁和顶围的设计变量分布图。

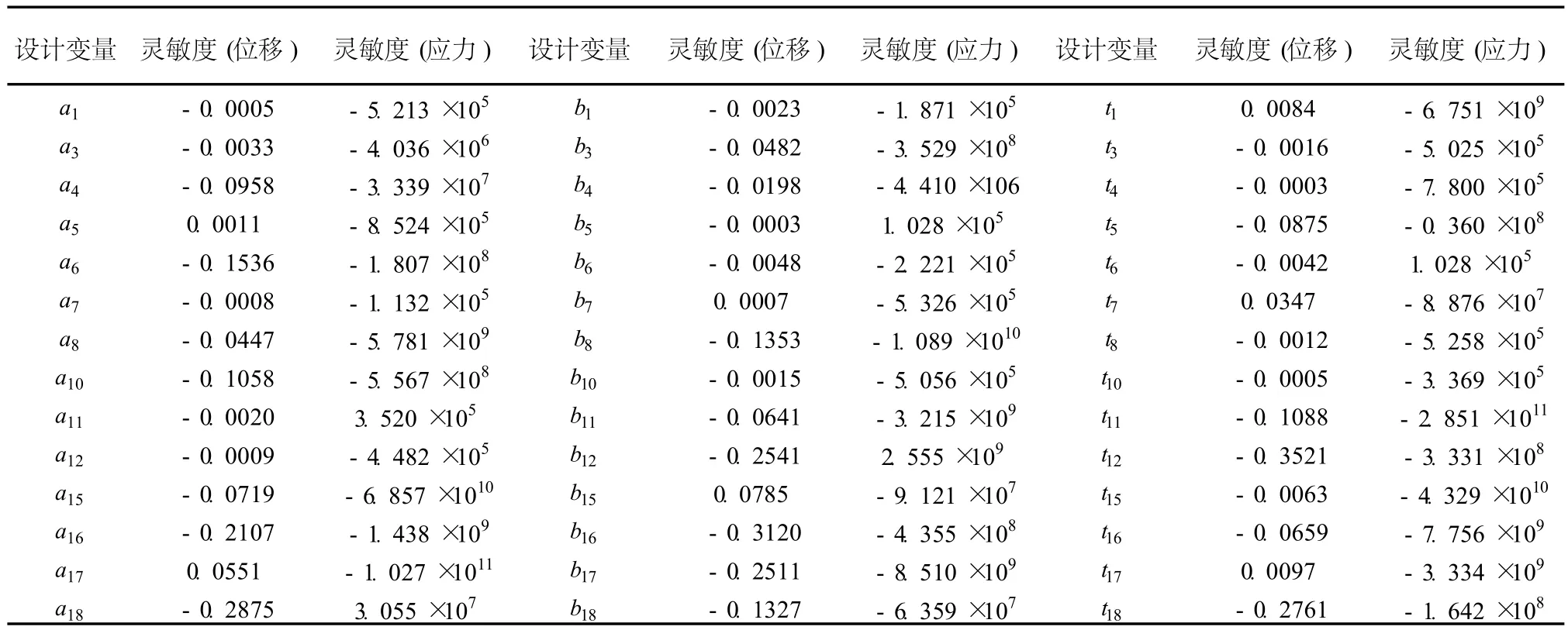
表 1 弯曲工况部分参数灵敏度分析结果

2.4 优化结果与分析

对模型进行优化计算,目标函数,即优化部分车身骨架质量的收敛情况如图 6所示;车身骨架的最大位移和车身的最大应力的变化情况如图 7、8所示。

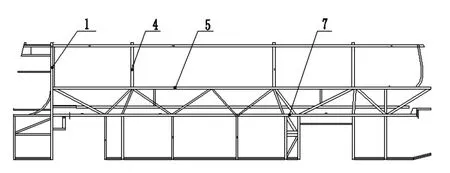
图 3 左侧围的设计变量

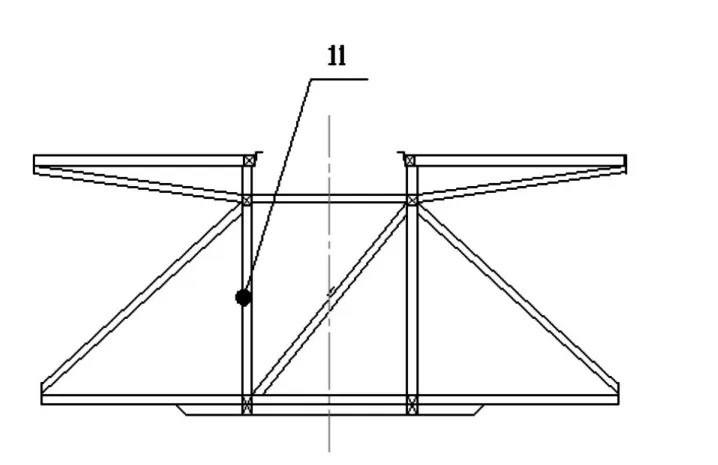
图 4 底架中段截面梁的设计变量

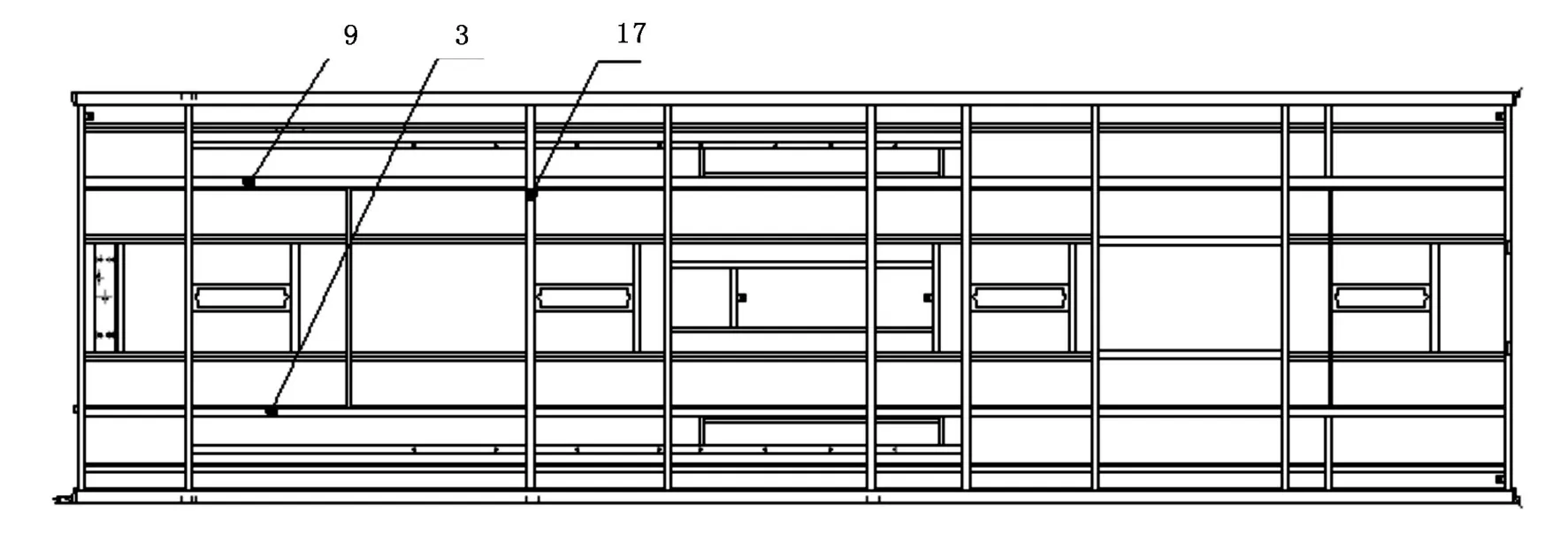
图 5 顶围的设计变量

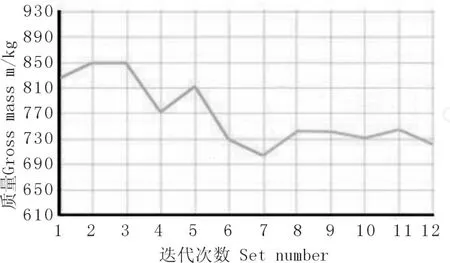
图 6 优化部分骨架质量变化情况

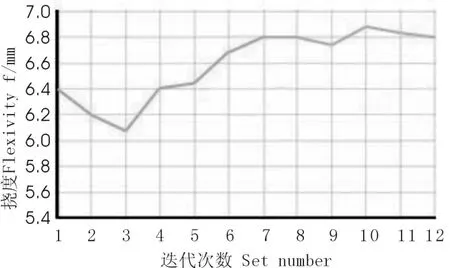
图 7 车身最大位移变化情况

本次分析共进行了 12次迭代计算。由图 6～图 8可以看出,前 6次迭代数值波动剧烈,以后的数据变化趋于平缓。第 7次迭代车身质量收敛最大,从优化前的 830kg减为710kg,车身总重 1980kg,减轻 6%。对于反映车身刚度的最大位移量由图 7可以看出,第 7次迭代最大挠度为 6.8mm,比优化前的 6.4mm增加 6.25%,挠度小于厂家要求的变化上限,也小于文献[8]中后置发动机客车的最大变形参考值10mm。由图 8可以看到,第 7次迭代结果车身构件的最大应力变化不大,由原来的 110 MPa增加到 116 MPa,增加 5.45%。车身为 16Mn,屈服强度为强度为 350MPa,安全系数较高[9]。

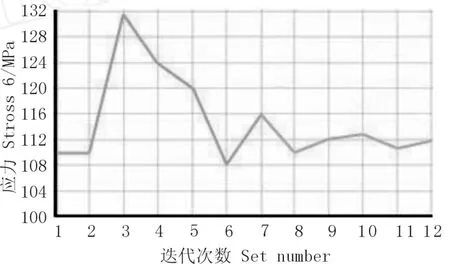
图 8 车身最大应力变化情况

综合图 6～图 8可知,客车车身质量的减轻是以增大车身最大位移量和最大应力为代价的。在客车车身轻量化的过程中,应协调车身最大位移、最大应力 (状态变量)与车身总质量 (车身总体积即状态变量)之间关系,在保证车身刚度、强度的同时降低车身构件最大应力及尽可能多的减少车身质量。

由于钢材型号有限,最终的轻量方案必须是在优化的基础上圆整后得到。表 3所示为部分截面尺寸变动情况。

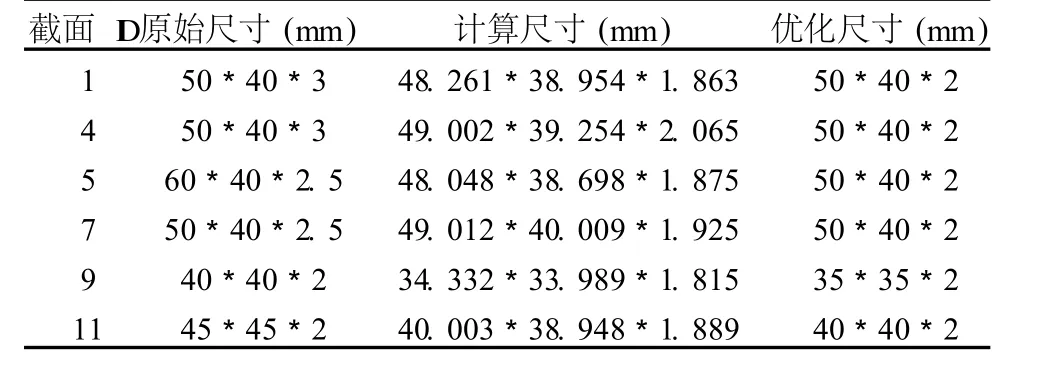
表 3 部分截面优化前后尺寸变化表

3.模态分析

车身结构不仅要有足够的强度和静刚度以满足其疲劳寿命以及使用要求,而且也应该有合理的动态特性以达到控制车身振动和噪声的目的。错开车身固有频率和激振频率,可以避免骨架共振现象的发生,进而有效提升乘客乘坐的舒适度,并且乘坐舒适度是衡量客车性能的重要指标。所以,对轻量优化前后的车架模型进行模态分析是非常必要的。

根据模态分析理论,对于高阶特征值系统的求解,往往需要耗费大量的计算时间。对于大型工程结构的客车车身来说,只需要了解前几阶的振型和频率,因为低阶振动对结构动力性能影响最大。表 2为优化前后前十阶车身固有频率值及其阵型的对比。

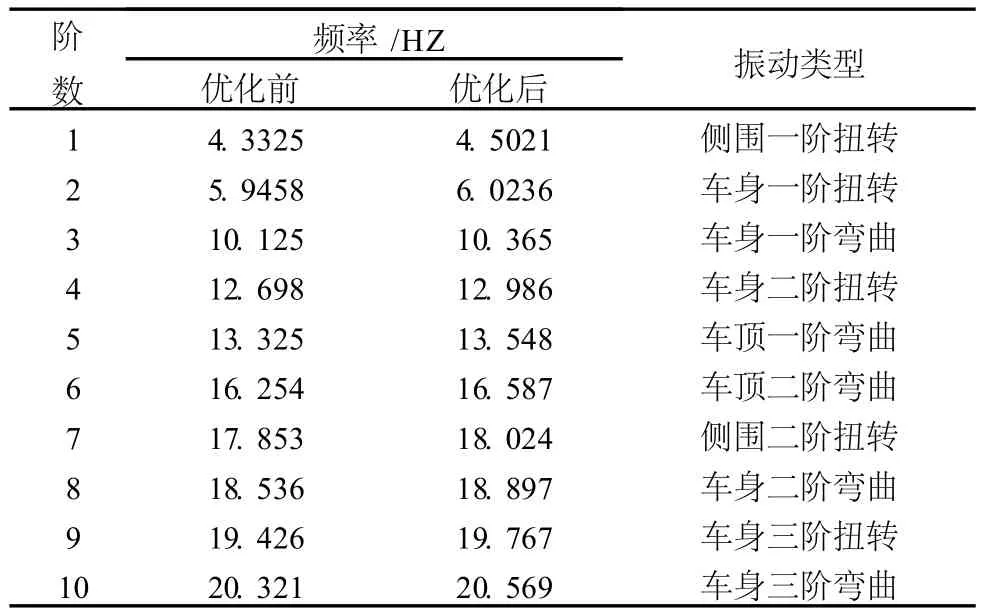
表 2 优化前后前十阶车身固有频率值及其阵型的对比

通过表 2比较可以发现,整车优化前后整车振动除了振幅值稍微上升以外,局部阵型并没有发生剧烈变化,说明优化后的刚度变化均匀。

由试验数据可知,该车身与悬架共振频率为 1.9-3.1HZ,发动机怠速频率约 17-25HZ,因此该车架的理想频率范围为 3.1-17HZ。该车车身一阶扭转频率为 6.0236HZ,一阶弯曲频率为 10.365HZ,可见车身低阶固有频率均符合理想固有频率。所以,优化后车架整体避免了共振现象的发生。

4.结论

本文以灵敏度分析方法对客车车身骨架实施了定量的轻量优化,而且模态计算显示优化结果符合设计要求,通过计算分析我们可以得出:

(1)在车架的应力值和位移值均满足设计要求的同时,车架总重减轻了 6%,优化效果明显,满足了厂家的要求。

(2)计算结果对轻量优化方案提供了切实可行的定量依据,改变了以往轻量方案凭借经验和感觉的方法,避免了设计的盲目性。

(3)灵敏度分析是确定优化过程设计变量的有效方法之一,是汽车车身结构优化设计的实用技术,对汽车设计有重要的意义。

[1]刘惟信.汽车设计[M].北京:清华大学出版社,2000.

[2]李辉.客车车身骨架有限元分析与轻量化改进设计[D].合肥工业大学,2006.

[3]张荭蔚.S WB6125低入口城市客车车身结构分析[D].上海交通大学,2002.

[4]石琴.大客车车身骨架结构强度分析及其改进设计[J].汽车工程,2007,29(1):87-92.

[5]孙营.灵敏度方法在汽车设计中的应用[J].湖北汽车工业学院学报,1999,13(4):67-70.

[6]王红霞,黄金枝.灵敏度分析在汽车车架模型修改设计中的应用[J].武汉汽车工业大学学报,2000,22(1):14-17.

[7]李黎明.ANSYS有限元分析实用教程 [M].北京:清华大学出版社,2005.

[8]GB/T 13043-2006.客车定型试验规程[S].

[9]吴浩皂.客车车身有限元强度分析载荷条件的确定[J].机械工程学报,1997,33(5):83-87.