蔡氏电路的实验制作

朱 雷,包伯成,卜沛霞,乔晓华

(江苏技术师范学院电气信息工程学院,江苏常州 213001）

蔡氏电路的实验制作

朱 雷,包伯成,卜沛霞,乔晓华

(江苏技术师范学院电气信息工程学院,江苏常州 213001）

本文以一个简单的经典蔡氏电路作为电子技术综合实训的实验制作电路,指导学生进行工作原理分析、状态方程建模、数值仿真、运算放大器形式的蔡氏二极管等效电路设计,以及实验观察。蔡氏电路的实验制作可以让学生从简单的电路中观察到丰富的非线性物理现象,可以巩固学生对已学内容的理解。

综合实训;蔡氏电路;混沌

0 引言

蔡氏电路是一种非线性混沌电路[1-3],它是以美国加州大学伯克利分校蔡少棠的姓命名的。蔡氏电路只含有四个基本元件和一个非线性电阻,实验电路制作简单。通过对一个电阻的调节,便可从电路中观察到周期极限环、单涡旋和双涡旋混沌吸引子的非线性物理现象。因此,蔡氏电路已成为在数学和物理实验方面演示混沌现象的一个范例。

近两年来,匈牙利学者Gandhi等[4]和Bilotta等[5]人把长期只有学者们关注的混沌这一富有挑战性的主题,延伸到了高中学生的学习活动中。他们分别组织高年级学生,进行蔡氏电路的实验制作,观察电路产生的复杂混沌现象,使学生的学习兴趣和动手能力有了很大的提升。

电子信息工程类专业学生在本科学习阶段进行的实验观察,大多是基于电参数(电压和电流)变量关于时间的二维平面观察,尚未开展过基于两个参数变量关于时间的三维空间观察。学生在四年本科课程完成后还不清楚两个正弦参数变量的相轨图是怎样的。因此,有必要在本科学习期间增加蔡氏电路的实验制作这一电子技术综合实训课程,让学生建立起空间观察概念,并对电路的非线性现象有一定的了解。笔者在部分电子信息工程类专业学生的电子技术综合实训中开设了蔡氏电路的实验制作课程,指导学生圆满地完成了该课程内容的学习,获得了令人满意的结果。

1 电路分析、建模和仿真

1.1 电路原理与数学建模

蔡氏电路由一个电感、两个电容、一个电阻和一个非线性电阻组成,如图1(a)所示。电路中电感L和电容C2构成了一个LC振荡电路,非线性电阻RN和电容C1并联后通过一个电阻R和振荡电路线性耦合在一起,形成了只有5个元件的能够产生复杂混沌现象的非线性电路。图1(b)是RN的伏安特性。

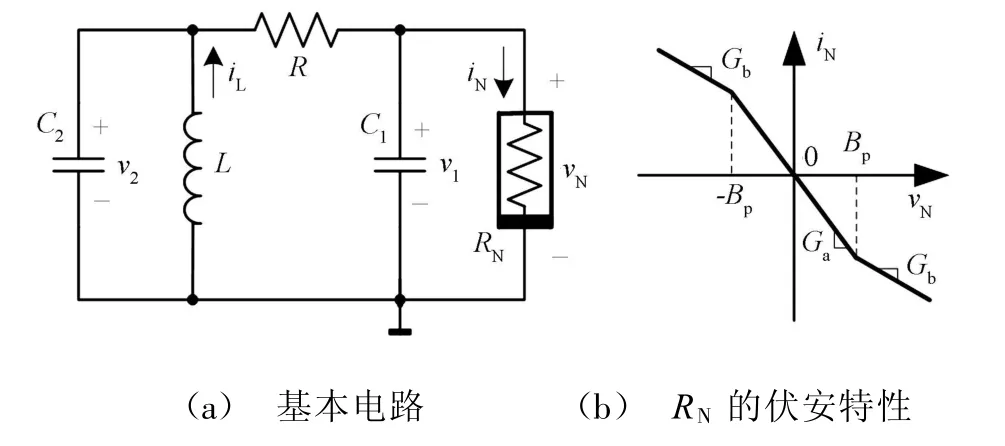
图1 蔡氏混沌电路和蔡氏二极管的VCR

蔡氏电路有三个动态元件,分别是电容C1、C2和电感L,对应的三个状态变量是电容两端的电压v1和v2,流过电感的电流 i L。根据电阻、电容和电感的元件伏安特性(即VCR),应用基尔霍夫电压、电流定律(KV L和KCL),可以导出基于这三个状态变量的微分方程组:

式中,f(v1)是描述蔡氏二极管R N(非线性电阻)的伏安特性,r是电感的寄生电阻值(图中没有画出)。

一般的蔡氏二极管是一个具有分段线性函数形式的非线性负阻,其伏安特性表达式为式中,Ga是内区间电导,G b是外区间电导,Bp是内外区间的转折点电压。

微分方程组式(1)是蔡氏电路的数学模型,它是一个三维连续自治混沌系统。在该系统中,在第一方程中有一个非线性项,因此它是一个非线性系统。已有大量文献对式(1)进行了无量纲处理,得到了只有三个控制参数的三维系统方程,称之为蔡氏电路方程。

1.2 数值仿真分析

利用Matlab仿真软件平台,可以对由式(1)描述的系统进行数值仿真分析。这里,选择ODE45算法对系统方程求解,很容易获得蔡氏电路状态变量的相轨图和时域波形图。

固定电路参数C1=10 nF,C2=100 nF,L=17.2 mH,r=0.5Ψ,G a=-757.58μS,G b=-409.09 μS和 B p=1.075 V,选择电阻值 R可变,数值仿真可得到在不同R时蔡氏电路的运行状态,如图2所示。图2(a)和图2(b)显示了蔡氏电路在电阻R=1.96 kΨ和R=1.945 kΨ时对应的周期1和周期2极限环,这里初始状态均为(0.1,0.1,-0.001);图2(c)和图2(d)则示出了在电阻R=1.91 kΨ时分别对应于初始状态(0.1,0.1,-0.001)和(0.1,0.1,0.001)时共存的单涡卷左、右混沌吸引子。

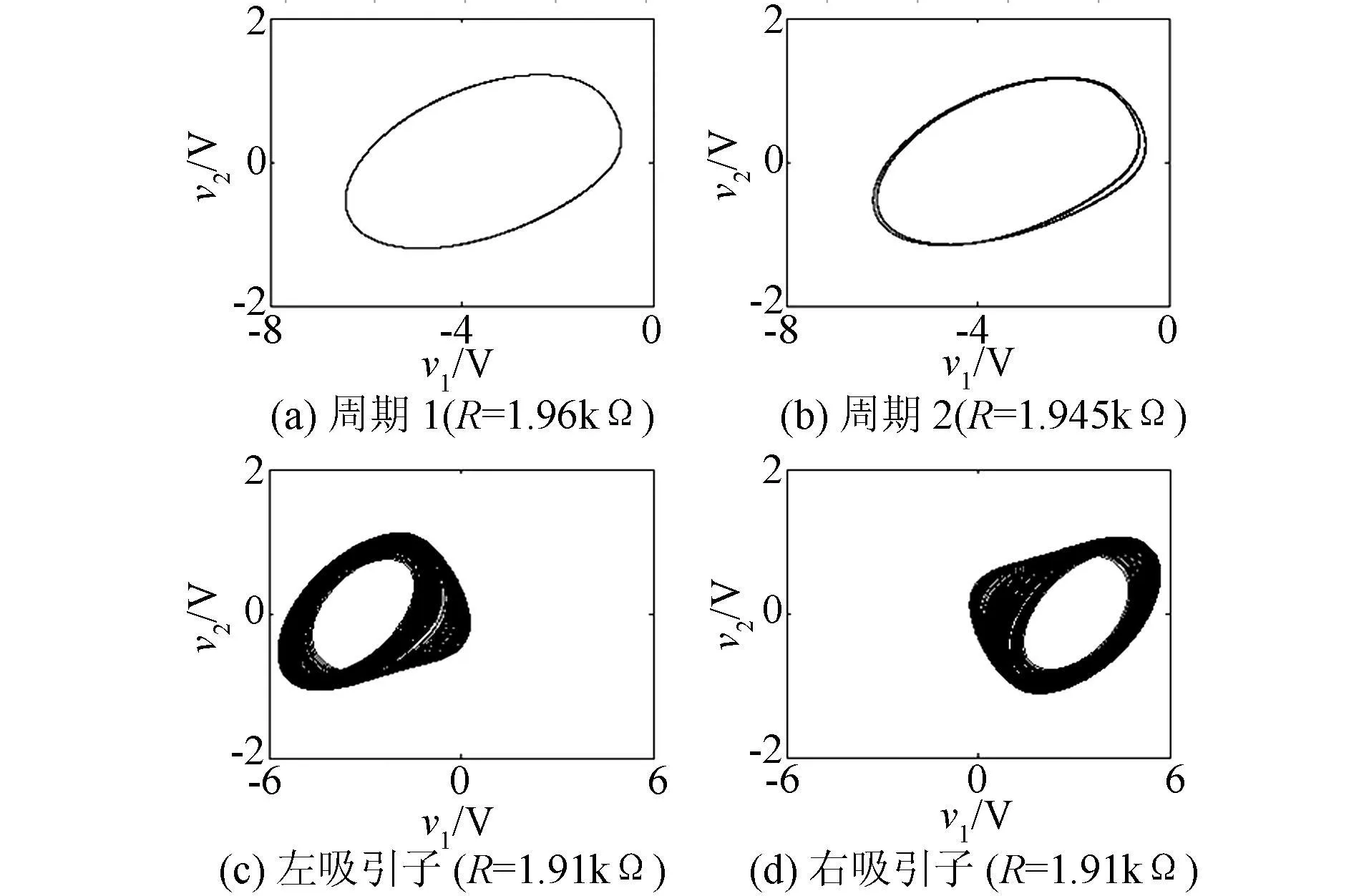
图2 蔡氏电路运行状态

当电阻R=1.57 kΨ时,蔡氏电路可生成一个典型的双涡卷混沌吸引子,如图3(a)所示,所对应的时域波形如图3(b)所示。数值仿真结果表明,随着电阻R逐渐降低,蔡氏电路的运行状态经历了从最初的一个渐近稳定点、周期振荡、谐波振荡到单涡卷混沌振荡和双涡卷混沌振荡的过程,最终趋于无穷发散。在这演变过程中,在出现双涡卷混沌吸引子之前,周期极限环和单涡卷混沌吸引子在相平面上所处的象眼位置取决于电感电流初始值的正负符号。符号为正为右吸引子或右极限环;符号为负为左吸引子或左极限环。

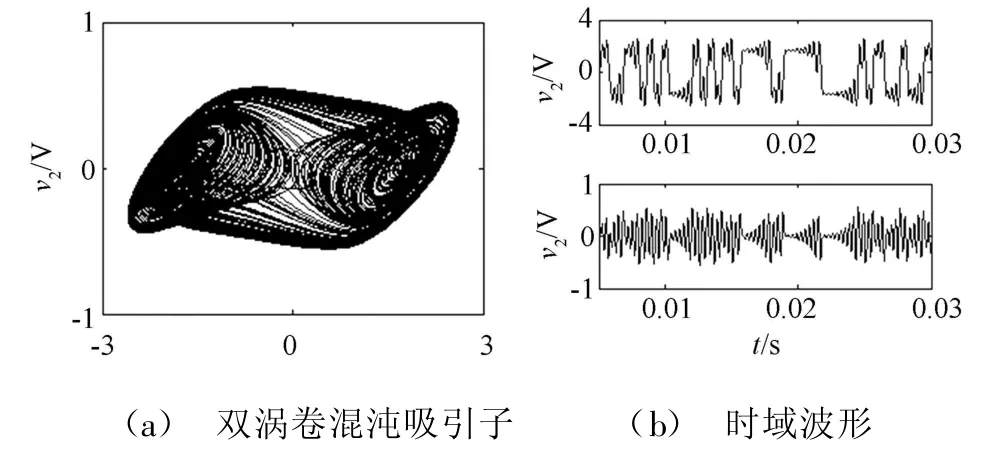
图3 典型混沌吸引子及其时域波形

2 设计制作和实验观察

2.1 蔡氏二极管等效电路设计

非线性元件(蔡氏二极管)是蔡氏电路产生混沌现象的重要元件,可采用多种方式实现,一种较为简单的实现电路如图4所示。图中,R N是由两个运算放大器和六个电阻组成的等效电路实现的,可看成是两个非线性电阻RN1和RN2并联而成。利用运算放大器的输出饱和电压特性,可实现由式(2)描述的等效电路伏安关系[6]。

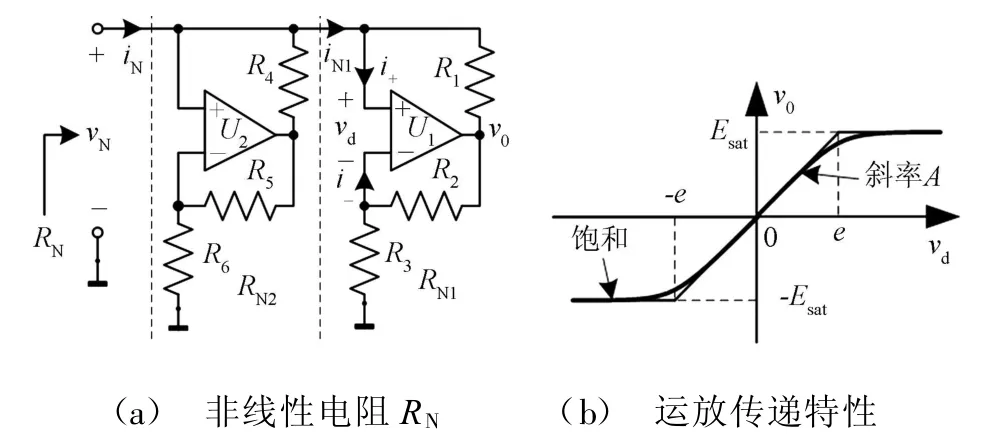
图4 蔡氏二极管等效电路实现和运算放大器传递特性

这里,以非线性电阻R N1的等效电路实现分析为例,设E sat是运算放大器的饱和电压,并令R1=R2,经推导得

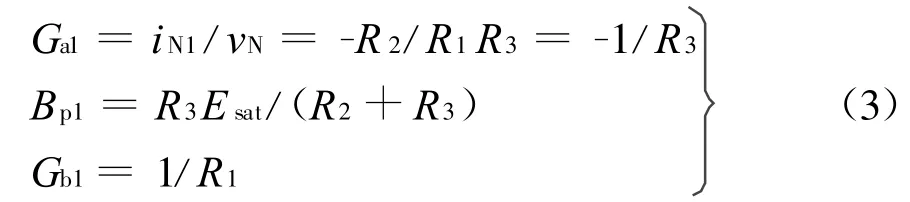
由式(3)可以画出R N1的伏安关系曲线如图5所示,它是一条形似于N型的具有非线性负阻区域的特性曲线。

同样地,令R4=R5,可以得到描述非线性电阻R N2的关系式:

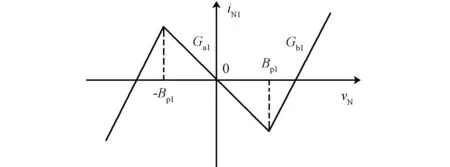
图5 R N1的VCR

两个非线性电阻RN1和RN2并联后,构成了一个具有五段分段线性函数形式的非线性电阻。与式(2)作比较,由图4(a)等效电路实现的蔡氏二极管的电路参数为

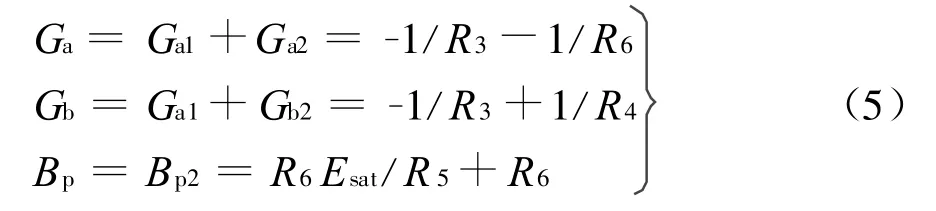
2.2 电路制作和实验观察

在实际制作调试图4所示的蔡氏电路过程中,可以分如下步骤进行。

首先,选定型号TL082CP集成运算放大器,工作电源设定为±9V。选择R1=R2=220Ψ,R4=R5=22kΨ,R3=2.2kΨ,R6=3.3kΨ。由式(5)可计算得 Ga=-757.58μS,Gb=-409.09μS 。实验测得Esat≈7.5V,计算得到B p≈1.075V。选用上述给定值的误差范围为±1%的精密电阻元件,就可以实现蔡氏二极管功能的非线性电阻RN。

为了实现图1所示的电路元件,我们自行绕制电感线圈,经测试电感值L≈17.2mH,电感线圈的寄生电阻r=0.5Ψ;选择两只精度较高的独石电容,电容值分别为C1=10nF,C2=100nF;另选择一只阻值可调的精密电位器R,用于实验观察时调节电阻值。

实验观察设备采用泰克双通道数字示波器,通道1测试图1(a)电路中电容C1端电压V1,通道2测试电容C2端电压V2。在电位器调节到不同阻值时对应的实验输出的相轨图如图6所示。当电位器阻值R=1.58kΨ时,在示波器上可分别观察到蔡氏电路所产生的混沌吸引子及其两路时域波形图,如图7所示。

由于分立元器件的离散性以及仪器的测量误差等,实验中蔡氏电路不同的运行状态所对应的电位器阻值与上述数值仿真时所选取的电阻值略有差异,但两者运行状态的演变趋势一致。

图6 蔡氏电路运行状态

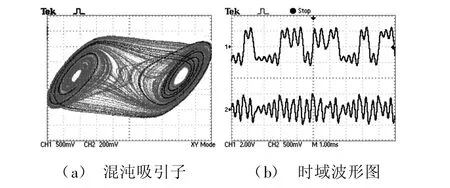
图7 混沌吸引子及其时域波形实验输出

3 结语

本文介绍的蔡氏电路的实验制作包含了电子信息工程类专业课程的重要内容,把它作为电子技术实训内容可以让学生进一步理解专业课程内容有着启迪意义,有利于培养学生的实际动手能力和科技创新思维。

三阶蔡氏电路是一个三维混沌系统,所产生的非线性物理现象与普遍存在于自然界的具有“蝴蝶效应”的混沌现象是完全一致的。由于非线性电路产生的混沌信号已在信息工程领域得到了广泛的应用[7]。因此,熟悉一定的非线性电路与系统的理论并了解混沌信号的具体产生电路和应用领域,对学生今后从事技术开发工作有一定的作用。

[1] E.Bilotta,P.Pan tano,F.Stranges.A gallery of Chua attractors:Part I[J].International Journal of Bifu rcation and Chaos,2007,17(1):1-60

[2] T.Matsumoto.A chaotic attracto r from Chua's circuit[J].IEEE Trans.on Circuits and Sy stems,1984,31(12):1055-1058

[3] G.Q.Zhong,F.Ayrom.Periodicity and chaos in Chua's circuit[J].IEEE Trans.on Circuitsand Sy stems,1985,32(5):501-503

[4] G.Gandhi,G.Cserey,J.Zerozek,T.Rosk.Anyone can build Chua's circuit:H ands-on-experience w ith chaos theory for high school students[J].International Journal of Bifu rcation and Chaos,2009,19(4):1113-1125

[5] E.Bilotta,E.Bossio,P.Pan tano.Chaos at school:Chua's circuit for students in junior and senior high school[J].International Journal of Bifu rcation and Chaos,2010,20(1):1-28

[6] R.Barboza,L.O.Chua.The fou r-elem ent Chua's circuit[J].In ternational Journal of Bifurcation and Chaos,2008,18(4):943-955

[7] Z.Liu,X.H.Zhu,W.H u,F.Jiang.Principles of chaotic signal radar[J].International Journal of Bifurcation and Chaos,2007,17(5):1735-1739

Experimental Implementation of Chua's Circuit

ZHU Lei,BAO Bo-cheng,BU Pei-xia,QIAO Xiao-hua

(Schoolo f E lectrica l and In formation Eng ineering,Jiangsu Teachers University o f Technology,Changzhou 213001,Ch ina)

Regarding a sim ple classic Chua's circuitas an experiment circuit ofelectronic technology comprehensive training,students are guided to perform operating p rincip le analysis,state differential equation modeling,numerical simulation,equivalent circuit design of Chua's diodew ith operationalamp lifier form,and experimentalobservations.Chua's circuit experiments can letstudentsobserve abundantnonlinear phenomena from the simp le circuit,and the understanding of the students to the already learned contents is further consolidated.

comprehensive training;Chua's circuit;chaos

G424;TN 702;TN 752

B

1008-0686(2011)02-0078-04

2010-08-12;

2010-12-23 基金项目:江苏省自然科学基金项目(批准号:BK 2009105)

朱 雷(1979-),男,硕士,讲师,主要从事非线性电路与系统的研究,E-m ail:dxzl@jstu.edu.cn

包伯成(1965-),男,博士,研究员,主要从事混沌信息动力学、非线性电路与系统的研究,E-mail:mervinbao@126.com

卜沛霞(1989-),女,本科生,研究方向为非线性电路与系统,E-mail:s08314101@smail.jstu.edu.cn

乔晓华(1960-),男,学士,教授,主要从事非线性电路与系统的研究,E-m ail:ahqxh@126.com