Kosko型双向联想记忆与Hop field神经网络的关系

张建国,殷勤业

(西安交通大学电子与信息工程学院,陕西西安 710049）

Kosko型双向联想记忆与Hop field神经网络的关系

张建国,殷勤业

(西安交通大学电子与信息工程学院,陕西西安 710049）

深入理解Kosko型双向联想记忆(BAM)网络是学习使用其它双向联想记忆的基础。如果我们按照传统的方法介绍BAM网络,学生很容易产生两个疑问:能量函数为什么是定义的?BAM网络与H opfield网络的内在联系是什么?本文在说明Kosko型BAM网络就是一种特殊的 Hopfield网络后,从H opfield网络的能量函数出发推导出BAM网络的能量函数,从而揭示了它与Hopfield网络之间的内在联系。

Hopfield神经网络;双向联想记忆;能量函数

0 引言

“神经网络”是一门重要的研究生课程,部分高校也为高年级本科生开设。Hopfield神经网络[1]是一种应用广泛的单层反馈神经网络,可以用于优化计算和联想记忆。联想记忆在信号处理和模式识别等方面都有广泛的应用。Kosko型双向联想记忆(BAM)网络[2,3]是Hop field网络的一种典型应用,让学生深入理解它是正确理解其它双向联想记忆网络的基础。

大多数教材[4-6]都沿用了Kosko在文献[2]中的介绍方法,即直接给出BAM网络能量函数的定义,而不展开论述这样定义的理由是什么,且通过构造一个大的零块对角阵(即分块矩阵对角线上的方阵是零矩阵),可以将任意连接权矩阵对称化,这样双向联想过程就能转换为对一组增广状态向量的自联想记忆过程。但由于这些并非是文献[2]讨论的重点,因此教材都未进一步展开讨论。

按照传统的方法介绍Kosko型BAM网络,学生无法理解能量函数定义的理由,因此很难理解它的基本原理及其与H op field神经网络之间的内在联系。

本文从结构上说明Kosko型BAM网络就是一种特殊的Hop field神经网络从Hopfield网络能量函数出发,直接推出它的能量函数。从而揭示了二者之间的内在联系,使学生在学习后理解地更为深刻。而且,不需要证明BAM网络的能量在联想过程中的递减性。

1 BAM网络的传统介绍方法

设双向联想记忆网络需存储M对矢量,分别用(a i,b i),i=1,…,M表示,其中a i∈{-1,1}为N维列矢量,而b i∈{-1,1}P为P维列矢量。

Kosko型BAM 网络的结构如图1所示。其中,下层的N个神经元与矢量a相对应,而上层P个神经元与矢量b对应。图中的W表示由矢量b联想矢量a时的突触权重矩阵,而WT为矢量a联想矢量b时的突触权重矩阵,它是W的转置。W与WT是按Hebb规则学习得到的,即:

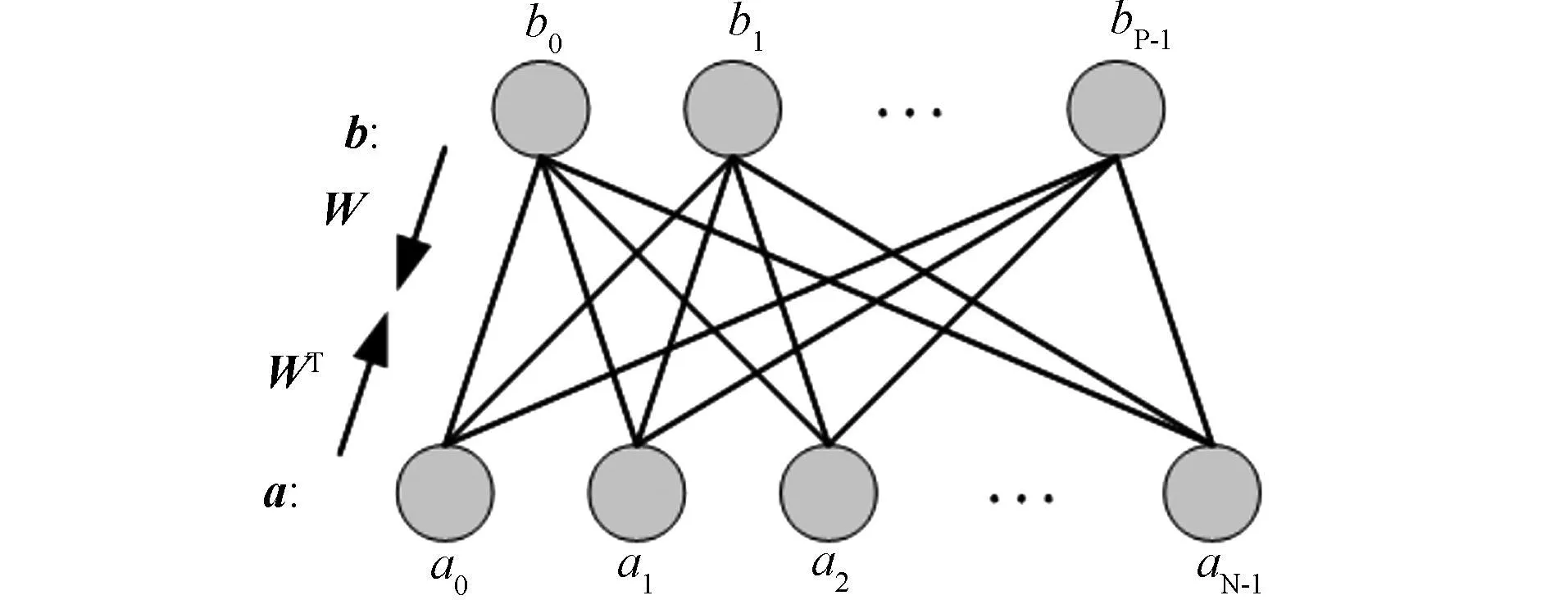
图1 双向联想记忆网络结构示意图

当由矢量b联想矢量a时,网络的演变过程为

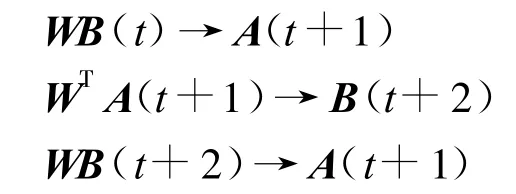
直到a、b均为稳定状态,演变过程结束。

定义Kosko型BAM网络的能量函数为

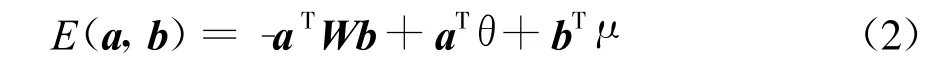
其中 ,θ=[θ0,θ1,…θN-1] 、μ=[μ0,μ1,…,μP-1]T分别表示与矢量 a、b对应的神经元的阈值(偏置电流)。

接下来,再给出描述BAM网络联想过程动态特性的差分方程。以b联想a为例,对应a向量的神经元的净输入为

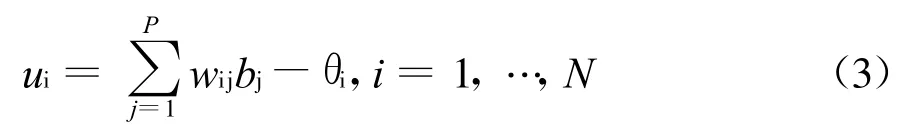
则有

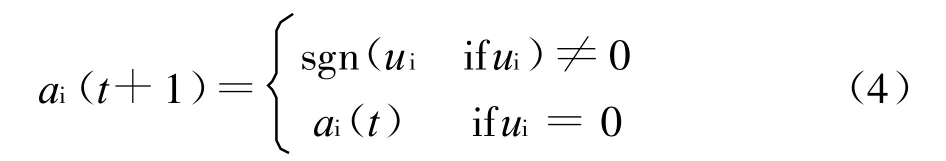
其中,符号函数sgn(·)为神经元功能函数。从式(4)可见,如果联想过程中神经元ai的输出发生了变化,则 Δa i=a i(t+1)-a i(t)与u i具有相同的符号。

不失一般性,假设从t时刻到t+1时刻,网络由矢量b联想矢量a,则联想前后网络的能量变化为

若联想过程中神经元ai的输出保持不变,则Δa i=0;若发生变化,由前述可知Δa i与u i有相同的符号,因此ΔE ≤0。当且仅当所有神经元输出都不变时,ΔE=0,此时网络稳定,输出即为联想结果。

按照上述方法讲解Kosko型BAM网络,学生通常问的第一个问题是如此定义能量函数的理由是什么?而第二个容易问到的问题是 BAM网络与Hop field网络之间有什么内在的联系?

2 从Hop field神经网络到BAM网络

Hop field利用模拟电子线路构造了单层反馈型人工神经网络的电路模型,并建立了电路的能量函数[1]。Hopfield网络的特点是每个神经元的输出要反馈给除自身外的其它所有神经元。其基本结构示意图如图2所示。图中神经元输入端的连接点表示各神经元的输出通过一个连接电导(突触)反馈到神经元的输入端。

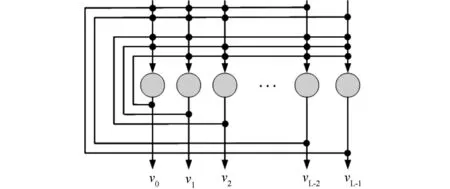
图2 Hopfield网络结构示意图

如果突触连接满足对称条件,且忽略变化较小的积分项,Hopfield网络的能量函数可以表示为

设L=N+P,则我们可以将L个神经元分成两组,分别含有N个和P个神经元。如果组内的任意神经元的输出都仅反馈到另一组神经元的输入端,而不反馈到本组任何神经元(包括该神经元本身)的输入端,如图3所示。显然,按此方式组成的网络仍然是一种对称Hop field神经网络。没有反馈意味着对应的突触连接系数等于零,因此该Hopfield网络的突触连接权矩阵可以表示为如下的分块形式:

其中,ON×N表示N×N维零矩阵,而W为N×P维矩阵。

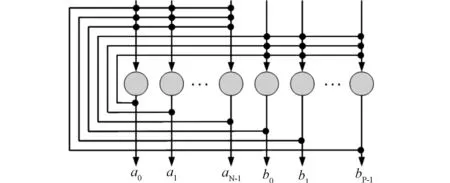
图3 双向联想记忆网络结构的变形

比较图3和图1可以发现,两者的神经元具有相同的连接形式。图1仅给出了两组神经元之间的反馈方式。而与图1相比,图3把两组神经元的输入、输出以及反馈连接表述得更为清楚一些。

如图3所示,我们用一组N个神经元表示BAM的a矢量,而用另一组的 P个神经元表示BAM 的b矢量。显然,式(7)中的W是P个神经元对N个神经元的反馈连接系数,它是由b联想a的突触权重矩阵,即W=W。与此类似,式(7)中的WT是由a联想b的突触权重矩阵,即WT=WT。所以

网络的输出矢量可以用BAM中定义的矢量表示为

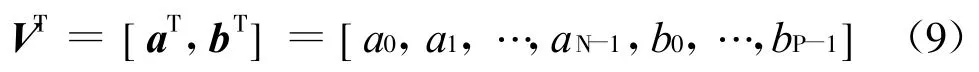
类似地,阈值向量可表示为

因此,Kosko型BAM网络是一种特殊的Hop field神经网络。

下面,我们从Hopfield网络的能量函数出发推导Kosko型BAM网络的能量函数。将式(8)～式(10)代入式(6),可得

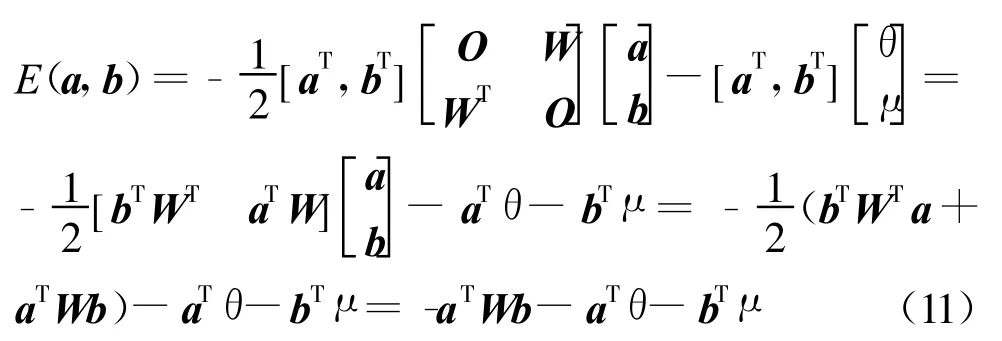
令阈值为零,即可得齐次BAM网络的能量函数为

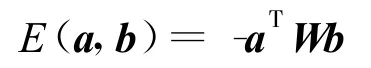
至此,我们从对称Hopfield网络的能量函数出发推出了Kosko型双向联想记忆网络的能量函数,阐明了能量函数定义的理由。

3 需要进一步说明的问题

1)能量函数中阈值项的符号问题

将推导出的式(11)和BAM能量函数的定义式式(2)比较,我们发现两者阈值项的符号正好相反。这是由于两种情况下的偏置电流(即阈值)的参考方向正好相反的缘故。

从式(3)可以看出,在讨论BAM 网络时,神经元的输入是反馈信号的加权和减去偏置电流,说明此时偏置电流的参考方向是流出节点的。

Hopfield根据KCL列出了如下节点电流方程:

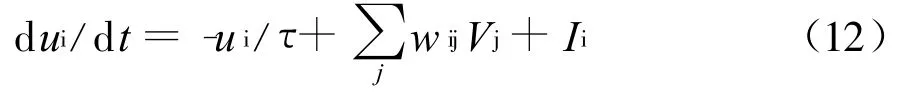
上式右侧的后两项说明神经元的输入是反馈信号的加权和加上阈值,这说明偏置电流的参考方向是流入节点的。因此,推导出的能量函数与BAM能量函数的定义式是一致的,二者并无矛盾。

2)网络联想时的初始化与迭代过程

我们知道,Hopfield网络也可以用于自联想记忆。基于上述理解,Kosko型BAM可以看作是对N+P维的矢量进行自联想记忆,从而把BAM与自联想记忆统一起来。下面,我们通过具体的例子说明网络的初始化与迭代过程。

假设从矢量b联想矢量a,BAM网络的初始输入记为b。在初始时刻,我们把b对应施加于代表矢量b的神经元的输入端对网络进行初始化,得到网络零时刻的输出为[O1×N,bT(0)]T。接下来,b(0)会反馈到矢量a神经元的输入端,在突触权矩阵的作用下,这个神经元的输出会变为 a(1)=sgn[Wb(0)],而代表矢量b的P个神经元的输出不变,我们将其记为b(1)=b(0)。到此为止,所有的神经元都有了初始输出,初始化过程完成。因此撤除加在矢量b输入端的b,网络开始进入迭代阶段。

根据Hop field网络的迭代方程,可以得到下一时刻网络的输出为

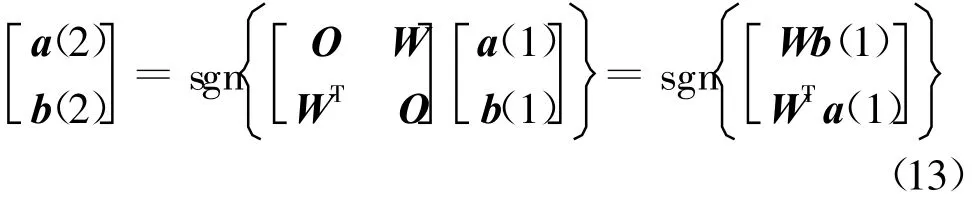
根据初始化过程,在结束时有:a(1)=sgn[Wb(0)]及b(1)=b(0),因此,上式中的a(2)=a(1),即从第1时刻到第2时刻相当于由矢量a联想矢量b,对应矢量a的神经元的输出不变。同理,下一次迭代实际上是由矢量b联想矢量a,对应矢量b的神经元的输出不变,即b(3)=b(2)。

如此循环迭代,直到所有神经元的输出不再改变,即Hop field网络达到稳定状态。此时输出的矢量a和b即为由输入b开始联想得到的矢量对。

3)网络迭代过程中能量的递减性

前面已经说明了Kosko型BAM网络实际上是一种特殊的 Hopfield神经网络。Hop field已经证明了,随着时间的推移,Hop field网络在状态空间中总是朝着能量函数减小的方向运动,当网络到达稳定状态时能量函数取极小值。这就说明BAM网络的能量随着时间的推移也是减小的,稳定时取极小值。因此,不需要再次证明能量函数的递减性。

4 结语

本文给出了一种Kosko型双向联想记忆网络的讲授方法。该方法揭示了Kosko型BAM网络与Hop field网络之间的内在联系,同时阐明了 BAM网络能量函数定义的原因,有助于学生深入理解这两种网络。近几年在对本校研究生的授课中采用了该方法,从学生的答疑和考试情况来看,均说明学生对BAM网络有了更深入的理解。

[1] J.J.Hopfield.Neu rons with graded response have collective compu tational p roperties like those of two-state neurons[J].Proc.Natl.Acad.Sci.1984,81(5):3088-3092

[2] Bart Kosko.Adaptive bidirectional associativememories[J].Applied Optics.1987,26(23):4949-4960

[3] Bart Kosko.Bidirectional associative mem ories[J].IEEE T rans on systems,MAN and cybernetics.1988,18(1):49-59

[4] 杨行峻,郑君里.人工神经网络[M].北京:机械工业出版社,1992

[5] 高隽.人工神经网络原理及仿真实例[M].北京:机械工业出版社,2003

[6] 韩力群.人工神经网络教程[M].北京:北京邮电大学出版社,2006

Relation between Kosko Bidirectional Associative Memories and Hop field Networks

ZHANG Jian-guo,YIN Qin-ye

(School of Electronic and In formation Eng ineer ing,X i'an Jiaotong University,X i'an 710049,Ch ina)

Kosko Bidirectional Associative Memory(BAM)network is one of the most fundamental BAM networks.When it is introduced w ith the traditional descrip tion,students usually have tw o questions,why theenergy function is given asa definition and what is the relation between Kosko BAM and Hopfield networks.In this paper it is show n at that first Kosko BAM network is just one type of Hopfield neural networks,and then the energy function of BAM is naturally acquired based on the energy function of Hopfield netw ork.Thereby the relation of themis exposed.

Hop field artificial neuralnetworks;bidirectionalassociativememories;energy function

TP183

A

1008-0686(2011)02-0098-04

2010-08-14;

2011-02-21

张建国(1971-),男,硕士,讲师,主要从事信号处理方面的教学和科研工作,E-m ail:jgzhang@mail.xjtu.edu.cn

殷勤业(1950-),男,博士,教授,主要从事神经网络理论及其应用和移动通信系统等方面的教学和科研工作。