基于统计分析的有限元模型修正
秦玉灵,孔宪仁,罗文波
(1.哈尔滨工业大学 卫星技术研究所,哈尔滨 150001;2.北京空间飞行器总体设计部,北京 100094)
0 引言
有限元模型修正技术在航空航天工程中应用广泛,高精度的有限元模型是准确进行结构力学特性分析的基础。但由于建模误差及实际结构在使用过程中的损伤等因素的影响,有限元模型计算结果与实测结果间总存在差异。利用结构实测响应修正有限元计算响应,使得修正后有限元模型计算响应值与试验测量值一致的过程即为有限元模型修正过程[1]。修正过程充分利用结构试验和有限元分析两者优点,用少量的试验数据对有限元模型进行修正,修正后模型可以代替实际结构进行多种分析,节约试验成本和时间。
用有限元软件的优化功能直接进行模型修正时,由于每次修正量的变化都要重新调用有限元软件计算,因此计算效率较低。近年来响应面方法开始在模型修正领域被广为应用,其基本思想是用多项式等构造响应面对原结构进行模拟,以较少的试验代价得到可接受的结果,在工程中有重要应用价值[2-3]。响应面模型构造过程需要对模型中的待修正参数进行筛选,用正交设计方法设计试验,并用统计分析方法中的方差分析选择模型参数中对响应影响程度大的参数作为待修正参数。响应面模型形式简洁,易于与粒子群算法等优化算法融合,修正效率高,但一组响应面只能对应一组分析过程,因此将响应面修正后参数代入原模型,可以进行多种力学特性分析,提高了分析效率。
本文用某雷达卫星简化有限元模型计算基于正交设计的各水平参数下模态频率,用方差分析确定待修正参数并构造二次响应面模型,用最小二乘法确定多项式系数,以响应面计算结果与实测结果的差值构造适应度函数并用其引导含混沌搜索机制的改进粒子群算法对待修正参数的偏移量进行寻优,修正后参数代入原有限元模型得到修正模型。修正后模型计算所得测试频段内模态频率与基准模型一致,且能以一定精度预测测试频段外的模态频率,从而证实了基于响应面和改进粒子群算法的模型修正方法的有效性。
1 正交试验设计及响应面构造
正交试验设计方法是一种研究多因子多水平试验问题的重要数学方法。该方法根据正交性从全面试验中挑选出“均匀分散,整齐可比”的样本点,是一种高效经济的试验设计方法[4]。正交试验完成后可用方差分析评价参数显著性,从中选择显著性高的参数进行后续计算。
方差分析(analysis of variance,ANOVA)又称“变异数分析”或“F检验”,其基本思想是将数据总离差平方和分解为各因素及误差的离差平方和,再用F检验确定各因素影响的显著性水平,从而确定待修正参数。模型参数A的F值检验按公式(1)进行[5]。
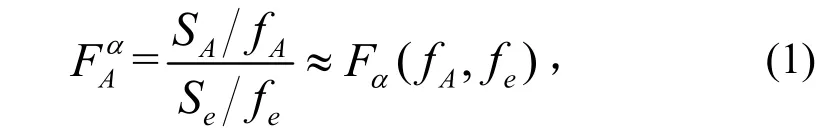
式中:α为置信度;FA为因素A 的显著性水平;SA和Se为因素A和误差e的偏差;fA为因素A和误差e的自由度。
响应面法是用多元多项式或非多项式模型(如人工神经网络)来描述系统自变量和响应特征的复杂关系,从而替代有限元仿真和其他复杂模型进行更有效设计或计算的一种方法。响应面表达式一方面要尽可能简单,方便计算;另一方面又要考虑到能灵活反映各种真实曲面形状,拟合精度和效率是评价响应面建模方法好坏的重要标准[6]。二阶多项式响应面形式简洁,准确性高,在工程模拟中应用广泛,其形式为
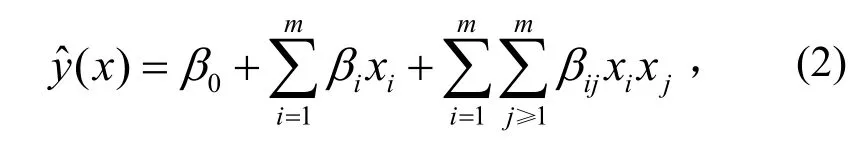
响应面模型质量可用两个标准检验,即均方根误差(root mean squared error,RMSE)的相对值和决定系数R2。
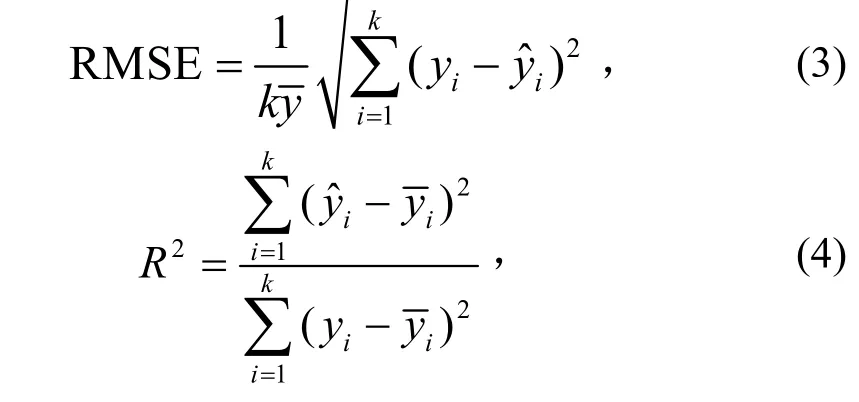
2 引进混沌搜索机制的粒子群算法
粒子群算法(particle swarm optimization,PSO)通过模拟鸟群觅食过程中的迁徙和聚集行为实现对问题的优化。算法中的每一个粒子都代表搜索空间的一个解,先随机初始化每个粒子的位置和速度,然后粒子在自身及整个种群最优位置的引导下飞向最优解[7-9]。标准粒子群算法中粒子速度和位置进化公式为

式中:pi,d(t)和pgd(t)分别为第t次迭代时第i个粒子第d维分量的最优位置和群体最优位置;常量c1>0,c2>0(c1+c2≈4),分别代表对自身经历的最优位置和种群最优位置的记忆能力;r1、r2用来增强粒子飞行的随机性以保持种群的多样性,r1∈rand(0,1),r2∈rand(0,1);ω 为惯性因子,ω>0,当 ω较大时群体以较大步长进行全局搜索,较小时算法以较小步长进行细致局部搜索。
混沌搜索的基本思想是:把混沌变量线性映射到原设计空间,然后利用混沌变量进行有效搜索。由于混沌的遍历性,混沌优化算法易跳出局部最优解,是一种很好的搜索机制[10-11]。Logistic映射是一种常用的混沌映射,其表达式为
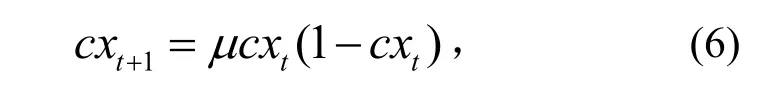
式中:µ为控制变量,一般在(3.5699456,4]之间取值;cx∈(0,1)。µ= 4时为完全混沌状态,此时cx在(0,1)范围内遍历。Logistic映射有3个不动点——0.25,0.5,0.75,在参数设定过程中应避免使用这些不动点。
混沌变量cx与普通变量x可以通过式(7)和式(8)进行往复映射。

式中:minx为设计空间中变量x的取值下限;maxx为取值上限。
引入混沌搜索机制的改进粒子群算法流程如图1所示。
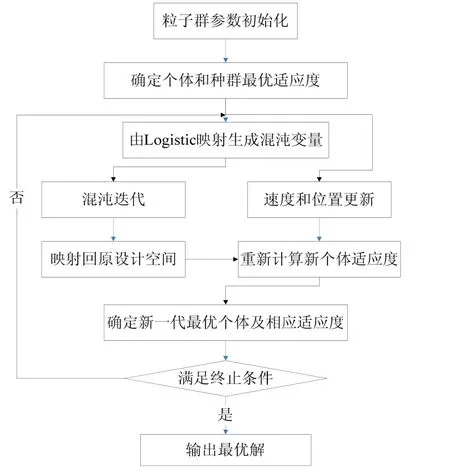
图1 引入混沌搜索机制的改进粒子群算法流程Fig.1 The improved PSO with chaos-search mechanism
3 卫星有限元模型修正
基于响应面方法和改进粒子群算法的有限元模型修正包括响应面模型的建立与粒子群算法的寻优两方面内容。其模型修正流程如图2所示。
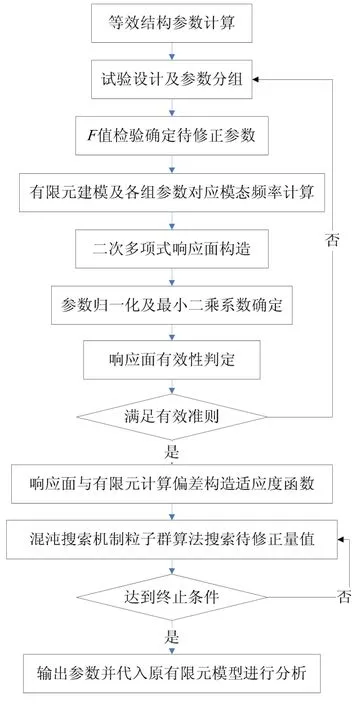
图2 基于响应面方法的模型修正流程Fig.2 Flow chart of the RSM-based model updating
1)用等效板理论计算构造卫星壁板和太阳帆板的蜂窝板的等效结构参数;
2)用正交试验设计方法进行试验设计,通过F值检验判定各结构参数对频率响应的影响,从而确定用于构造响应面的待修正参数;
3)用ANSYS中的SHELL63单元和BEAM4单元建立简化卫星模型并计算其在各组参数下的模态响应;
4)构造二次多项式响应面,参数归一化并用最小二乘法则确定响应面函数系数向量;
5)响应面模型有效性判定,若有效则进入下一步分析,否则返回第2步;
6)用响应面计算所得频率ˆy与有限元计算频率y的偏差构造适应度函数;
7)用带混沌搜索机制的粒子群算法修正结构参数;
8)判断是否满足终止条件,若满足则输出修正量,否则返回第7步继续计算;
9)将修正量代入有限元模型,模型计算质量得到改善,进行多种分析计算。
3.1 卫星简化有限元模型建立
某雷达卫星简化有限元模型如图3所示,卫星壁板和太阳帆板为蜂窝板结构,其等效板由ANSYS中的SHELL63壳单元建立,由等效板理论[12]计算所得壁板和帆板的等效参数均为:蜂窝板尺寸1 m×1 m,板厚req=0.06 m,等效弹性模量Eeq=831.4 MPa,等效泊松比µeq=0.3,等效密度ρeq=107 kg/m3。卫星箱体与蜂窝板之间由4根梁进行连接,用BEAM4梁单元建立,结构参数为:弹性模量E=70 GPa,密度 ρ=2.7×103kg/m3,泊松比 µ=0.3,截面积a =10-4m2,z向和y向抗弯惯性矩Izz=Tyy=10-8m4。
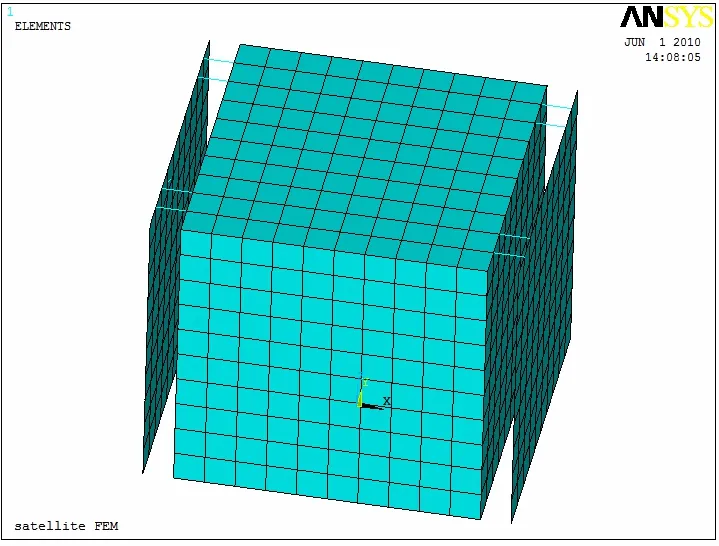
图3 卫星简化有限元模型Fig.3 Simplified FEM of the satellite
3.2 正交试验设计及待修正参数确定
对有限元模型中的4个等效结构参数req、Eeq、ρeq、µeq进行筛选,同时考虑结构损伤及阻尼材料的影响,将连接梁的3个材料参数E、ρ、a也作为待修正参数,每个参数取2个水平,即七因素二水平,水平1为7个参数原值,水平2为7个参数摄动后值(各减小20%)。正交设计方法设计试验时,首先用正交表从所有可能搭配中挑出若干必需的试验,然后再用统计分析方法对试验结果进行综合处理,可以减少试验次数,提高分析效率。本例选取正交表L8(27)设计8组试验数据如表1所示。
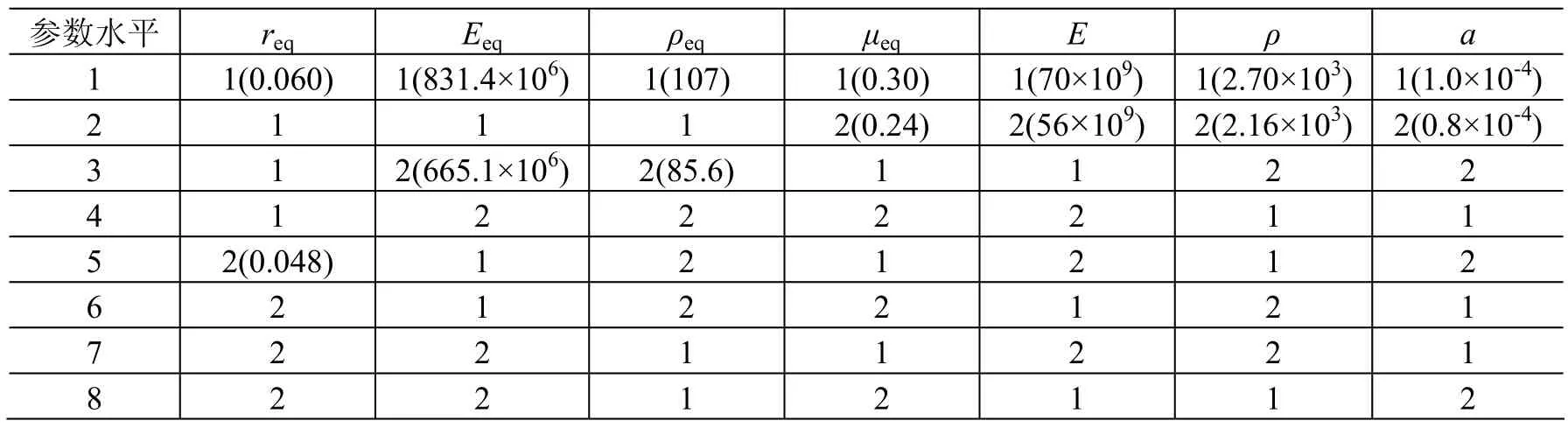
表1 不确定参数正交设计表Table 1 Orthogonal design for uncertain parameters
用有限元分别计算8组参数前6阶模态频率值,对计算所得的48个样本点进行方差分析。常用F(f,f )值检验水平有4个,即α =[0.25,0.10,αAe 0.05,0.01],各水平意义和符号见表2。方差分析过程中发现,ρ和a两个参数对模态频率影响最小,故将两者视为误差项,用于对其余5个参数的显著性水平进行计算。
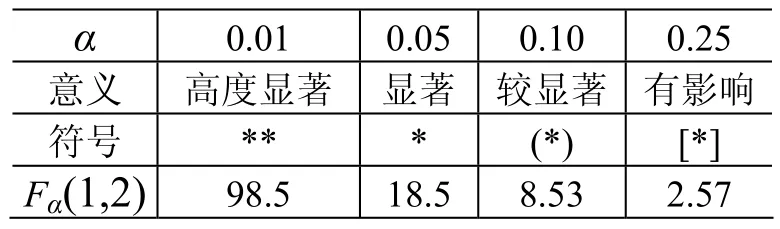
表2 显著性水平Table 2 Significance level
由表3的F值检验结果可知,req、Eeq和 ρeq对模态频率影响程度最高,E次之,µeq影响力最弱,由此选定板等效厚度req、等效弹性模量Eeq、等效密度ρeq及梁弹性模量E为待修正量。

表3 各参数显著性水平Table 3 Significance level of parameters
3.3 响应面构造及有效性检验
用F值检验确定的4个结构参数req、Eeq、ρeq和E构造响应面的完全二次多项式为
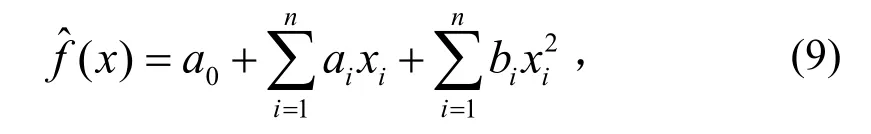
响应面模型有效性由相对RMSE和决定系数R2评价,如图4所示。
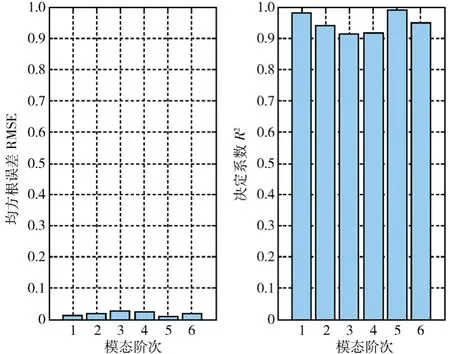
图4 响应面有效性评价Fig.4 Validity evaluation of the response surface
由图4可知,卫星前6阶模态的响应面计算值与相同结构参数的有限元计算值之间的RMSE均趋于0,决定系数R2均趋于1,响应面模型有效,可用于进一步分析计算。各阶模态拟合精度具体分析为:f1和f5拟合精度最高,原因在于对这两阶模态有影响的结构参数req、Eeq、ρeq和E都参与了响应面的构建;f3和f4拟合精度相对较差,原因在于对这两阶模态有影响的参数µeq未参与响应面构建。由此可见响应面构建中参数选择的重要性,在工程实际中可以对某重要模态单独分析其影响参数,构建相应响应面模型。
3.4 卫星模型修正及有效性检验
以参数水平(1,1,1,1)即x1=[req1,Eeq1,ρeq1,E1]所建有限元模型为基准模型M1,以参数水平(2,2,2,2)即x2=[req2,Eeq2,ρeq2,E2]所建有限元模型为待修正模型M2,两组结构参数的关系为x2=x1(1-20%)=x1(1+Δx), 其 中 Δx=[Δreq,ΔEeq,Δρeq,ΔE]为待修正量的偏差量,亦即粒子群算法搜索的目标解。模型结构参数如表4所示。
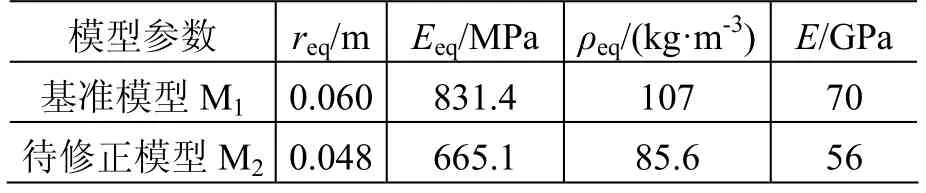
表4 模型结构参数Table 4 Structure parameters of the FEM
响应面模型修正中的适应度函数由基准模型M1计算所得模态频率f1和响应面模型S计算所得模态频率fˆ之间的差值构成,其可表示为
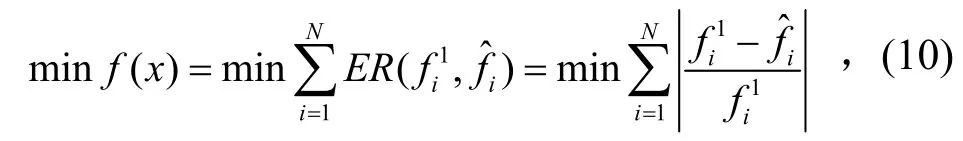
式中:N=6为模态频率阶数,该适应度函数的意义为使得各阶模态频率相对误差和最小;fi1(i=1,2,...6)为定值(基准模型M1计算所得模态频率);(i=1,2,...6)为响应面模型计算值,其值随待修正量x=[req,Eeq,ρeq,E2]的不断变化(由粒子群算法迭代搜索获得)而变化,至适应度函数值达到设定条件时,待修正量得到确定。
用带混沌搜索机制的改进粒子群算法对摄动后结构参数进行修正,每个粒子维数为D=4(对应4个待修正量),粒子群种群规模为N=50,即用50个粒子进行随机搜索,迭代次数设为Tmax=30。搜索空间范围(粒子位置x和速度v)由以下分析确定:任取待修正参数xi,设定其变化范围为原值(x1=[req1,Eeq1,ρeq1,E1])上下20%浮动,响应面构造过程中进行参数归一化得
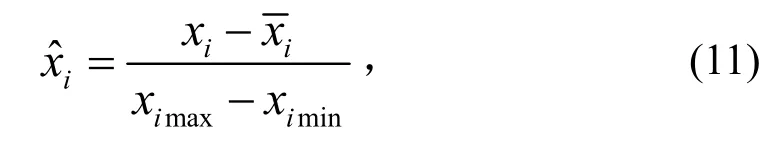
式中,ximax=(1+20%)xi1;ximin=(1-20%)xi1;为各水平参数平均值,则xi=(xi1+xi2)/2=0.9xi1。可得-0.25≤xˆi≤0.75,由此,粒子位置x和速度v变动范围-0.25≤x≤0.75,-0.25≤v≤0.75。
由于算法的随机性,用改进粒子群算法重复进行20次搜索,取各次搜索的适应度函数平均值绘制平均适应度函数收敛曲线;同时选各次搜索所得最优解的平均值作为修正量Δxˆ,将Δxˆ从归一化后的参数空间映射回原设计空间即可得到待修正参数的真实摄动量Δx;将Δx代入响应面模型和待修正的有限元模型得到修正后的响应面模型S1和修正后有限元模型M3;计算修正后模型M3的前6阶模态频率与基准模型M1比较,评价修正后模型对测试频段内模态频率的复现能力,同时为了考察修正后模型的预测能力,计算M3的7~10阶模态频率并与基准模型M1对比,分析修正后模型对测试频段外模态频率的预测效果。
由表5可知,用修正后参数建立的响应面模型S1和相同参数建立的有限元模型M3计算所得模态频率接近,证实了响应面模型代替有限元模型计算的可行性。由表6可知,修正后有限元模型M3的结构参数较待修正模型M2更接近基准模型M1,模型质量得到改善。同时由表5和图5可知:用摄动后所得待修正模型M2计算获得的模态频率明显偏离基准模型M1计算值,修正后有限元模型M3在测试频段内计算所得的前6阶模态频率与基准模型误差在1%以内(第3、4阶频率误差较大为0.93%和1.02%,与第3、4阶模态响应面构造中参数选择相对误差较大有关),测试频段外误差在3%~5%之间,大于测试频段内误差,但仍在可接受精度范围内。因此证实了响应面方法修正后的有限元模型不但能以高精度复现测试频段内模态频率,而且能以可接受的精度对测试频段外频率进行预测。
图6描述了重复执行带混沌搜索机制的改进粒子群算法20次迭代且每次迭代30个循环过程中的平均适应度函数收敛曲线。适应度值随迭代进行不断减小,意即修正后模型计算频率与实测频率之间差值随着迭代搜索过程的进行不断减小,粒子群在群体最优粒子的引导下逐渐向全局最优解靠近。将搜索到的最优解代入原有限元模型,所得模型计算模态频率能充分靠近实测值,证实了算法的有效性。
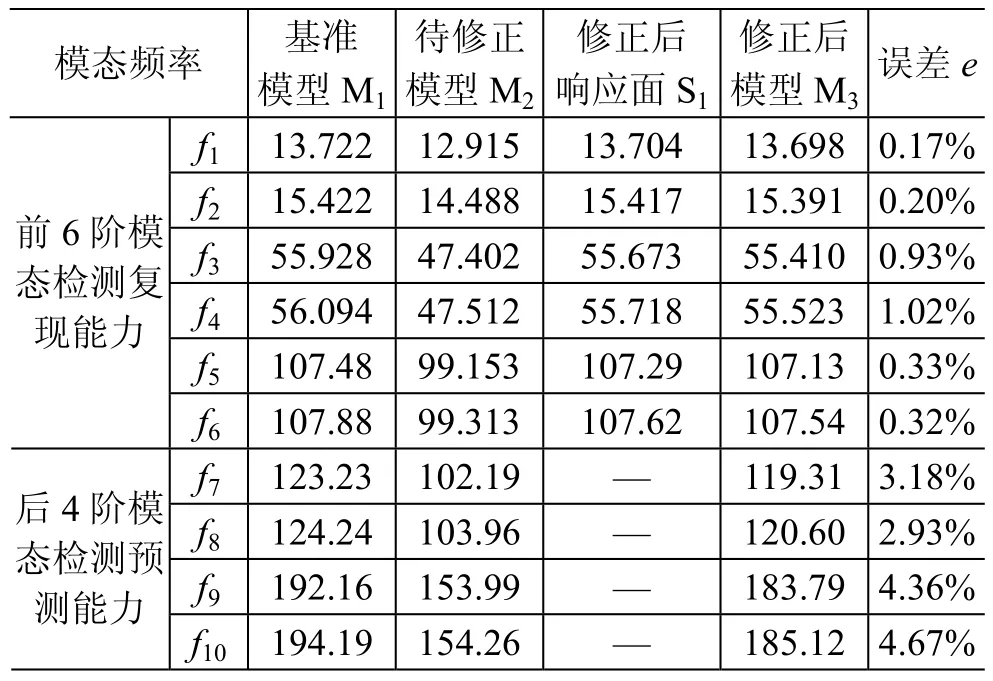
表5 响应面和有限元模型计算模态频率Table 5 Modal frequencies of the RSM and FEM
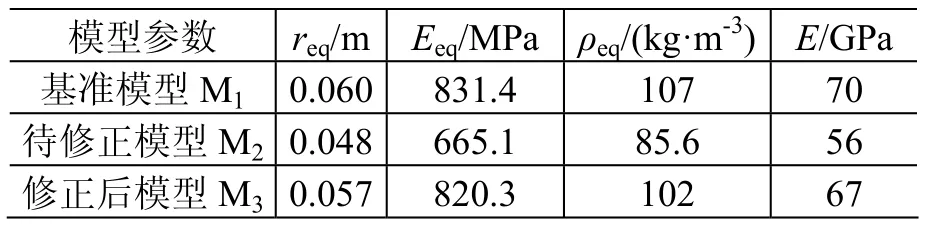
表6 模型参数对比Table 6 Comparison of the model parameters
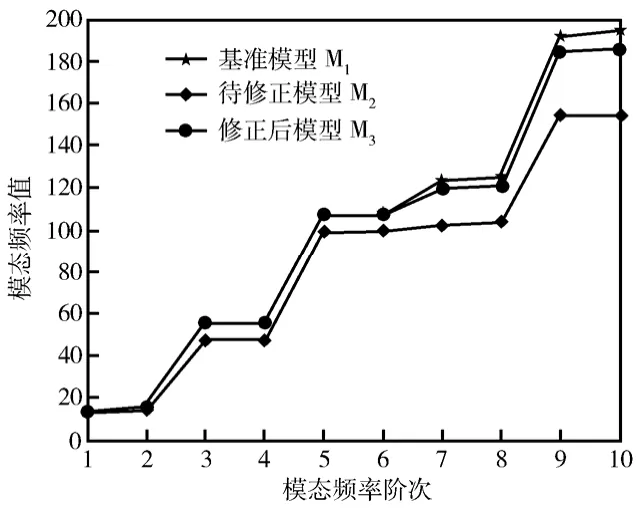
图5 模态频率对比Fig.5 Comparison of the modal frequencies
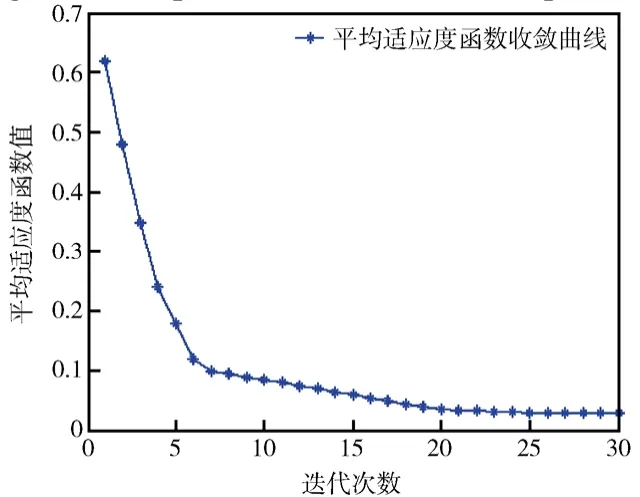
图6 平均适应度函数收敛曲线Fig.6 Mean convergence curve of the fitness function
4 结论
1)响应面模型计算所得的模态频率接近由相同结构参数的有限元模型计算所得频率,证实了响应面方法的可行性和可靠性。响应面模型便于与粒子群算法等优化算法相结合,用响应面模型代替有限元模型可以提高修正效率和模拟精度。
2)基于正交试验设计方法的响应面模型构造时,用F值检验结果作为选择待修正量的依据,待修正量的选取是决定响应面精度的重要因素,应通过改进试验设计方法或对现有方法增加补充条件以提高待修正量选取的准确性。
3)响应面模型的局限性在于一组响应面只能模拟一组响应数据与结构参数间的关系,要获得其他响应数据,必须再次通过多组试验数据获得另一组响应面,无法像有限元模型那样,通过一组结构参数,可以进行多种分析运算。因而用响应面模型修正所得结构参数重新建立有限元模型进行分析,可提高修正效率和计算效率。
(References)
[1]朱宏平, 徐斌, 黄玉盈.结构动力模型修正方法的比较研究及评估[J].力学进展, 2002, 32(4): 513-524 Zhu Hongping, Xu Bin, Huang Yuying.Comparison and evaluation of analytical approaches to structural dynamic model correction[J].Advances in Mechanics, 2002, 32(4):513-524
[2]任伟新, 陈华斌.基于响应面的桥梁有限元模型修正[J].土木工程学报, 2008, 41(12): 73-78 Ren Weixin, Chen Huabin.Response-surface based on finite element model updating of bridge structure[J].China Civil Engineering Journal, 2008, 41(12): 73-78
[3]Sobieski I P, Kroo I M.Collaborative optimization using response surface estimation[J].AIAA Journal, 2000,38(10): 1931-1938
[4]郭勤涛, 张令弥, 费庆国.用于确定性仿真的响应面法及其试验设计研究[J].航空学报, 2006, 27(1): 55-61 Guo Qintao, Zhang Lingmi, Fei Qingguo.Response surface method and its experimental design for deterministic computer simulation[J].Acta Aeronautica et Asrtonautica Sinica, 2006, 27(1): 55-61
[5]费庆国, 张令弥, 李爱群, 等.基于统计分析技术的有限元模型修正研究[J].振动与冲击, 2005, 24(3): 23-26 Fei Qingguo, Zhang Lingmi, Li Aiqun, et al.Finite element model updating using statistics analysis[J].Journal of Vibration and Shock, 2005, 24(3): 23-26
[6]Allen M S, Cambeves J A.Comparison of uncertainty propagation/ response surface techniques for two aeroelastic systems, AIAA 2009-2269[R]
[7]秦玉灵, 孔宪仁, 罗文波.GA-PSO组合算法模型修正[J].航天器环境工程, 2009, 26(4): 383-385Qin Yuling, Kong Xianren, Luo Wenbo.The model updating by GA-PSO algorithm[J].Spacecraft Environment Engineering, 2009, 26(4): 383-385
[8]孙木楠, 史志俊.基于粒子群优化算法的结构模型修改[J].振动工程学报, 2004, 17(3): 350-353 Sun Munan, Shi Zhijun.Structural model updating based on particle swarm optimization[J].Journal of Vibration Engineering, 2004, 17(3): 350-353
[9]Venter G, Sobieszczanski-Sobieski J.Particle swarm optimization[J].AIAA Journal, 2003, 41(8): 1583-1589
[10]林昆, 冯斌, 孙俊.混沌量子粒子群优化算法[J].计算机工程与设计, 2008, 29(10), 2610-2612 Lin Kun, Feng Bin, Sun Jun.Chaos quantum-behaved particle swarm optimization algorithm[J].Computer Engineering and Design, 2008, 29(10): 2610-2612
[11]侯力, 王振雷, 钱锋.基于混沌序列的自适应粒子群优化算法[J].计算机工程, 2008, 34(18): 210-212 Hou Li, Wang Zhenlei, Qian Feng.Adapting particle swarm optimization algorithm based on chaotics series[J].Computer Engineering, 2008, 34(18): 210-212
[12]夏利娟, 金咸定, 汪庠宝.卫星结构蜂窝夹层板的等效计算[J].上海交通大学学报, 2003, 37(7): 999-1001 Xia Lijuan, Jin Xianding, Wang Xiangbao.Equivalent analysis of honeycomb sandwich plates for satellite structure[J].Journal of Shanghai Jiaotong University,2003, 37(7): 999-1001

