不变本征算符法在含时二维双耦合谐振子系统中的应用
成泰民, 葛崇员
(沈阳化工大学数理系,辽宁沈阳110142)
最近,凌瑞良[1]等对不同频率、不同质量并含时双耦合谐振子系统进行了研究,并得到系统的简正频率的表达式及系统的严格波函数解.坐标与动量通过转动变换[1-2]对系统的哈密顿量进行退耦合处理.凌瑞良[1-2]等的工作没有给出很明显的系统的简正频率解析解表达式,并且对系统哈密顿量的退耦合处理较复杂.凌瑞良[3]等利用二次型理论及三次保对易的辛变换研究了三维各向异性耦合谐振子体系.徐世民[4]等利用有序算符乘积内的积分技术(IWOP)处理了两非全同谐振子体系,并推导出系统的波函数.上述系统的特点是系统的哈密顿量中只包含力学量的二次项.因此,上述系统的哈密顿量是线性的.范洪义[5-6]等对不同的哈密顿量系统,利用量子力学的不变本征算符法处理系统的元激发能量和能级差.为此,本文利用不变本征算符法推导明显的系统的简正频率解析解表达式及严格波函数,并讨论不变本征算符法对于线性哈密顿量系统的退耦合方面的普遍性和简捷性.
1 利用不变本征算符法对含时二维双耦合各向异性谐振子系统哈密顿量退耦合
考虑一般的情形,令m1(t)≠m2(t)、ω1(t)≠ω2(t)且坐标与动量耦合强度也均含时的双耦合谐振子系统的哈密顿量为:
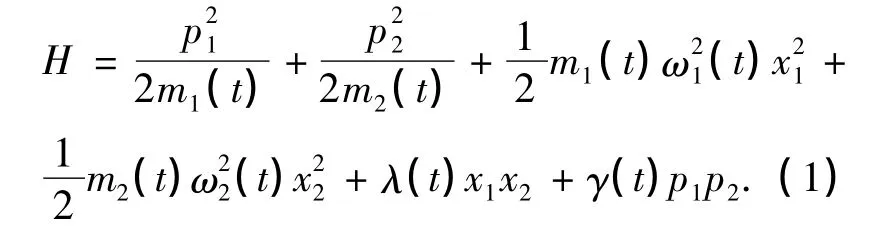
因为[xi,pj]=i¯hδij,[xi,xj]=[pi,pj]= 0(其中i,j=1,2),所以有如下对易关系:
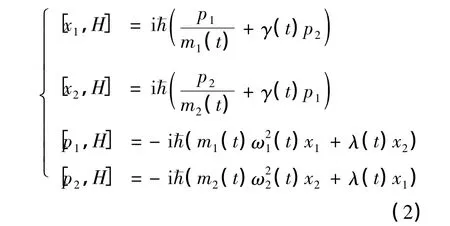
引入关于坐标的不变本征算符OCe=x1+ τCx2,由(2)式可得OCe与H的对易关系:
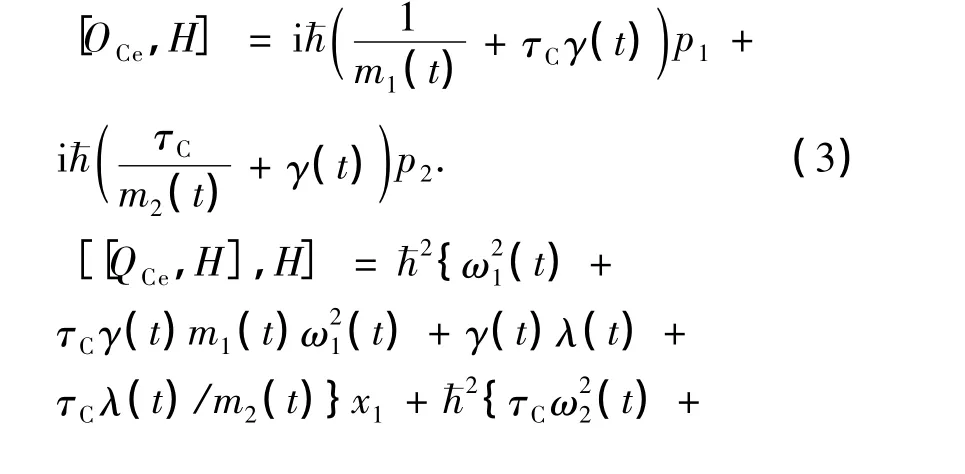
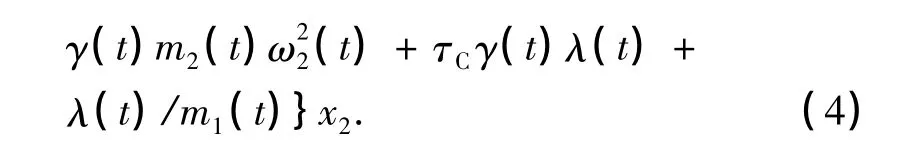
根据不变本征算符法可知:
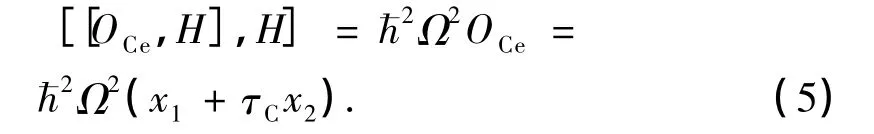
由(4)与(5)式可得:
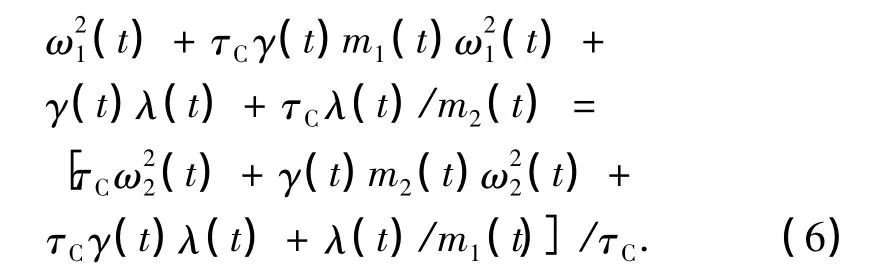
由(6)式可得:
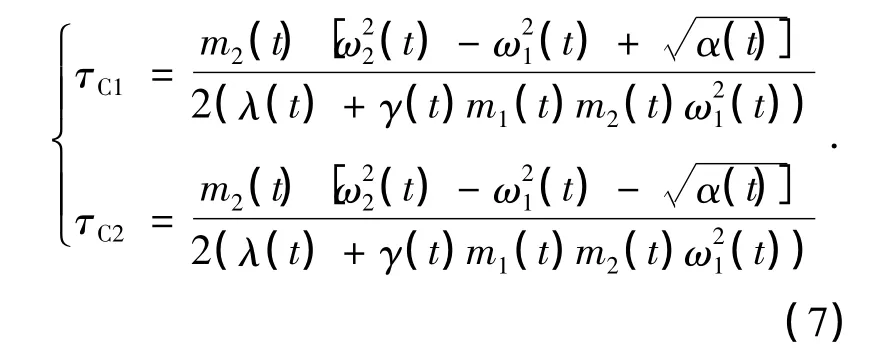
其中:
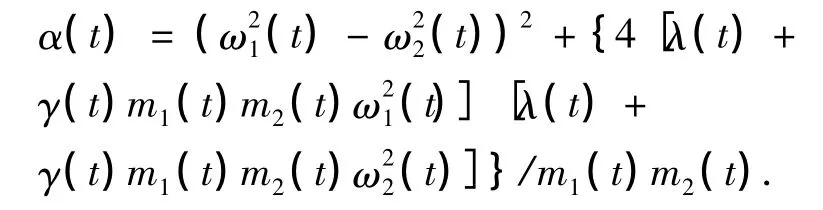
由(7)式可得关于坐标的不变本征算符:
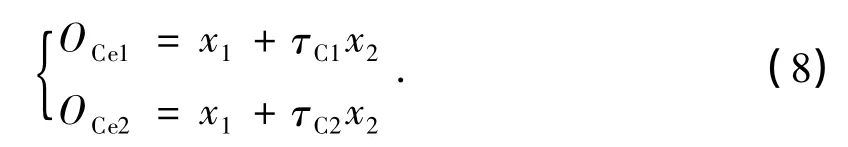
由(4)式、(5)式、(7)式可得系统的简正频率:
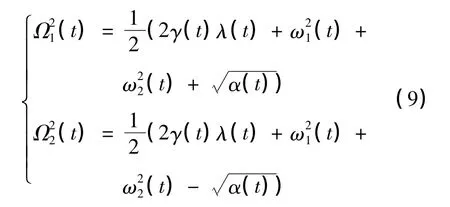
为得到与简正坐标对应的共轭动量,引入关于动量的不变本征算符OMe=p1+τMp2,由(2)式可得OMe与H的对易关系:
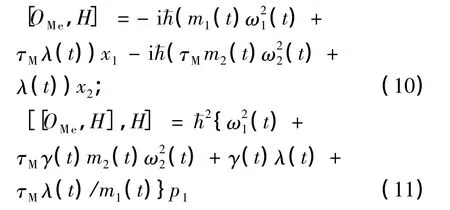
同理根据不变本征算符法可知:
[[OMe,H],H]=¯h2Ω2OMe=

由(11)与(12)式可得:
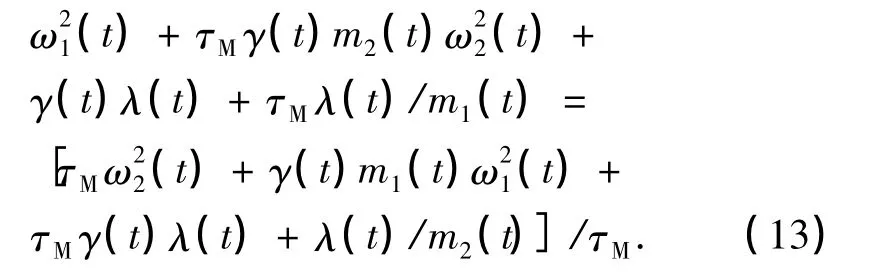
由(13)式可得:
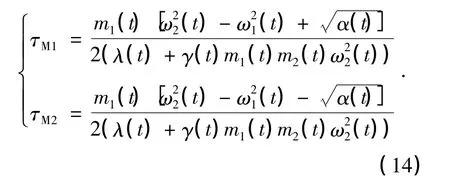
由(11)、(12)、(14)式,同样可得系统的简正频率(9)式,并由(14)式可得关于动量的不变本征算符:
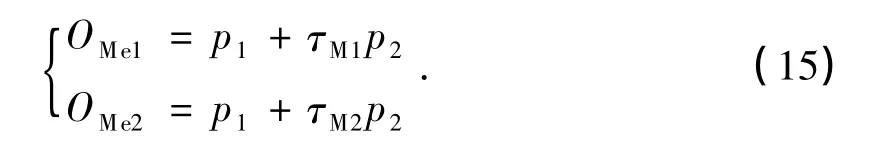
因为(8)式与(15)式分别对应简正坐标与其对应的共轭动量[7],为满足[Qi,Pj]=i¯hδij,[Qi,Qj]=[Pi,Pj]=0,对(8)式与(15)式的系数进行处理可得:

(16)式的逆变换为:

把(17)式代入(1)式可得:
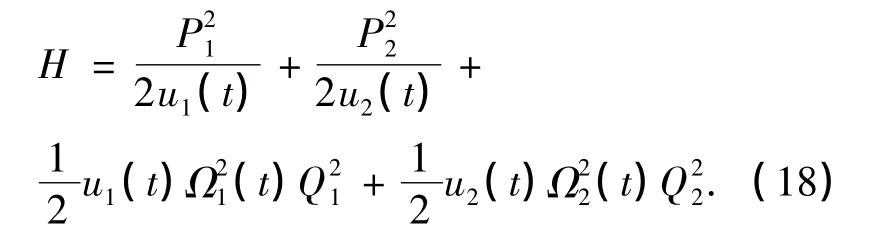
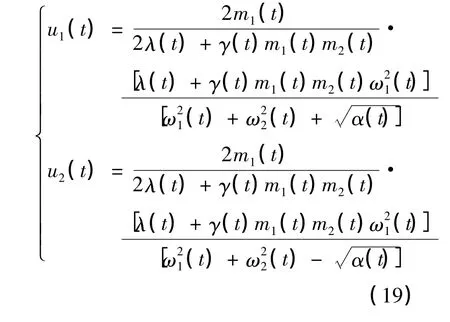
2 严格波函数的确定
将(18)式改写成:

其中:
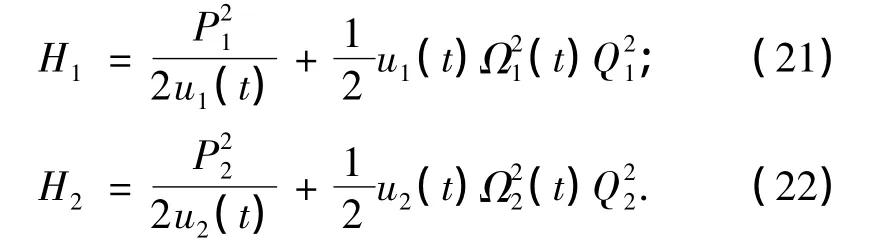
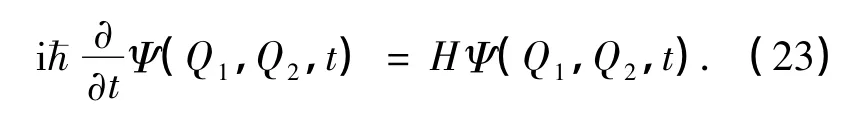
利用分离变量法,令:
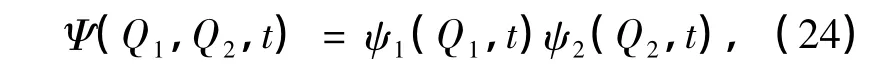
那么,可得:
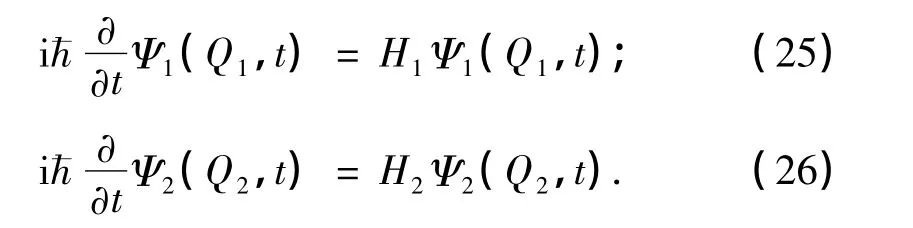
系统的薛定谔方程为:
根据(16)式、(19)式和文献[1-2]的处理方法及步骤,可得系统的严格波函数为:
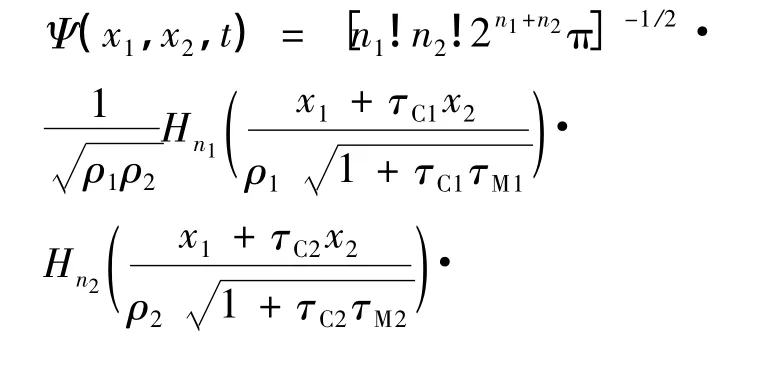
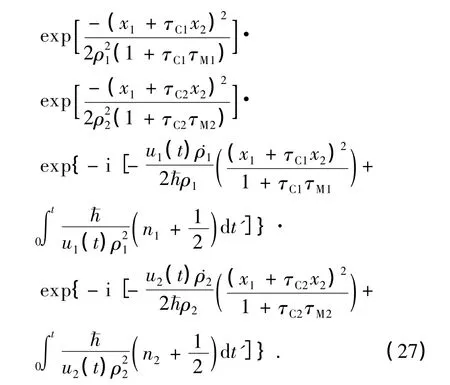
其中ρ1和ρ2由相应的辅助方程决定:
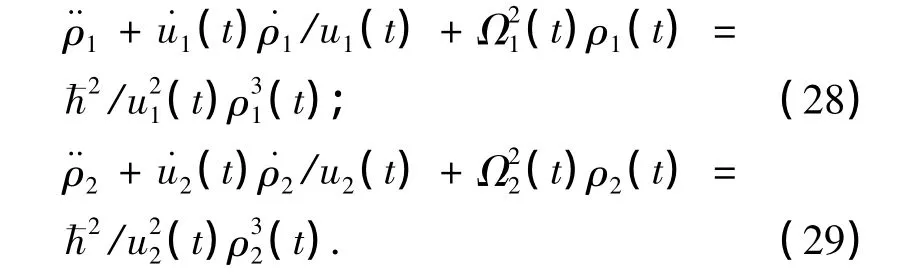
(27)式对应的能量本征值为:
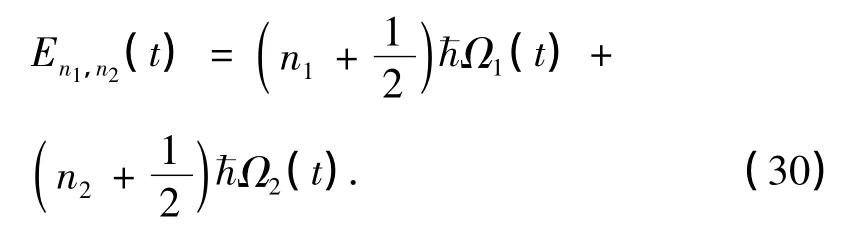
3 讨论
以两谐振子的质量和简正频率均相等且含时的系统为例,讨论不变本征算符法在含时二维双耦合各向异性谐振子系统处理中的正确性、简捷性、普适性.当
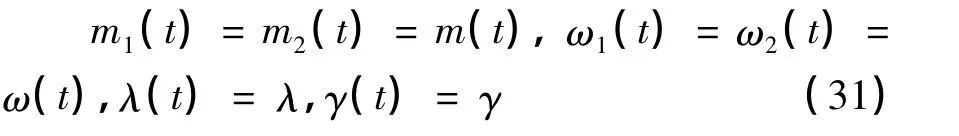
时,把(31)式代入到(7)、(9)、(14)、(16)、(19)、(27)式,可得:
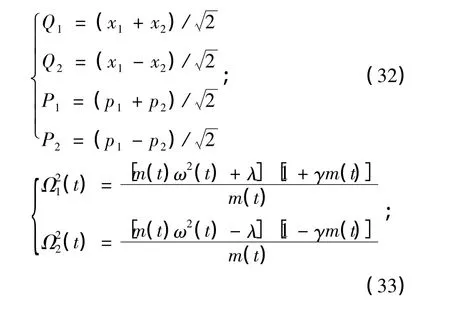
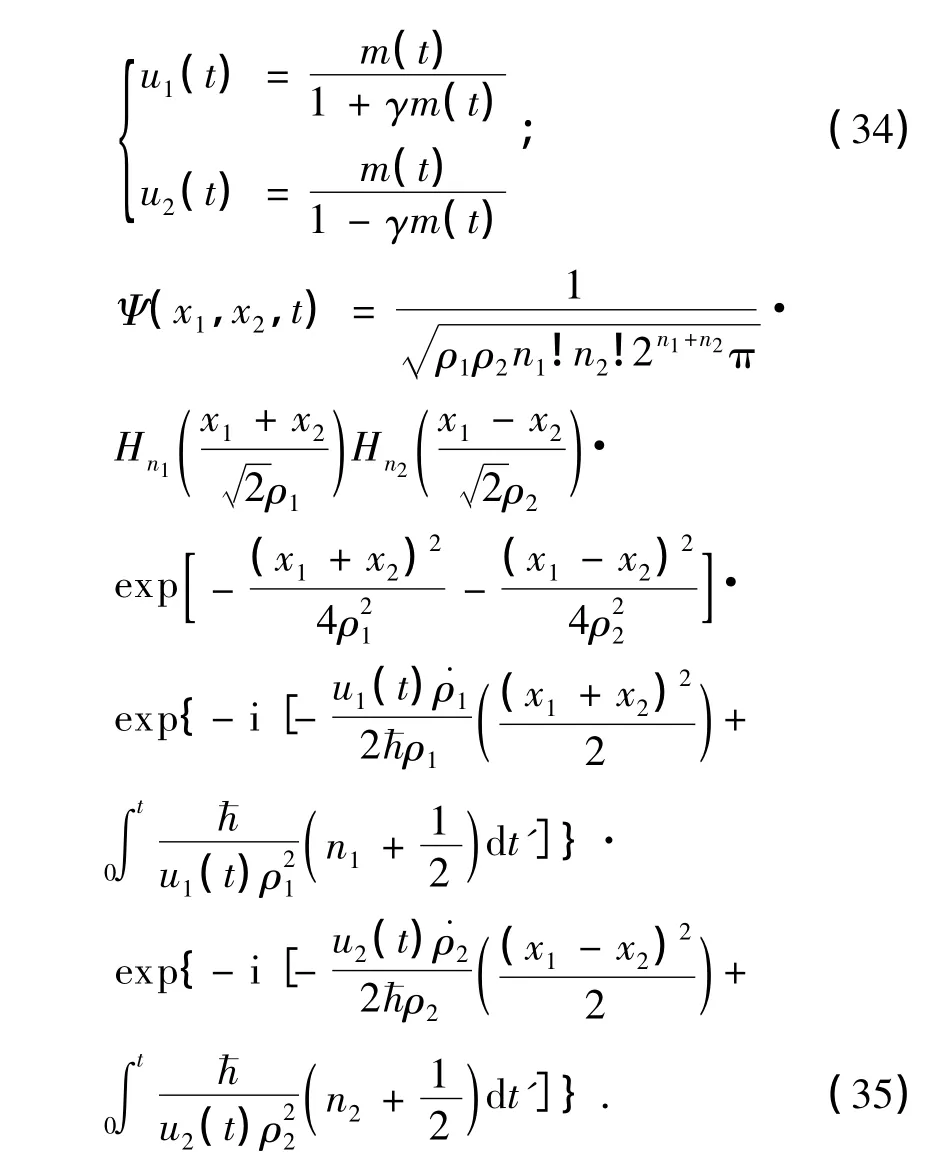
(32)~(35)式与文献[1-2]的结果相比较完全相同.
4 结论
根据以上推导及讨论可知:对于线性哈密顿量系统,利用不变本征算符法进行退耦合非常简捷,而且能够得到明显的系统简正频率的解析表达式,也不涉及耦合项前系数为零等处理.只要体系的哈密顿量中只含有力学量的二次项(线性化)时,利用“不变本征算符”方法计算体系的元激发能量非常简捷.因此,原则上利用“不变本征算符”方法也可计算多维多耦合各向异性谐振子系统的简正频率解析解与波函数.
[1] 凌瑞良,冯金福,胡云.含时二维双耦合各向异性谐振子的严格波函数[J].物理学报,2010,59(2): 759-764.
[2] 凌瑞良,冯金福.质量和频率均含时的耦合谐振子的严格波函数[J].物理学报,2009,58(4):2164-2167.
[3] 凌瑞良,冯进,冯金福.三维各向异性耦合谐振子体系的量子化能谱与精确波函数[J].物理学报,2010,59(12):8348-8358.
[4] 徐世民,蒋继建,李洪奇,等.两体组合坐标表象的建立、性质及应用[J].物理学报,2008,57(12): 7430-7437.
[5] Fan HongYi,Li Chao.Invariant‘Eigen-operator’of the Square of Schrödinger Operator for Deriving Energy-level Gap[J].Phys.Lett.A,2004,321(2):75 -78.
[6] Fan HongYi,Wu Hao.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method[J].Modern Physics Letters B,2005,19(26):1361-1366.
[7] 黄万霞.简正坐标的另一种求法[J].大学物理,2008,27(9):14-15.

