基于并发序列模式的偏序模式挖掘
逄玉俊, 刘 英, 陈未如
(沈阳化工大学计算机科学与技术学院,辽宁沈阳110142)
判断事务的偏序关系[1]在生活中应用越来越广泛,这个偏序关系是由一些相互关联的事务及其上的序关系构成,这里的序关系主要包括事务之间经常顺序出现的、经常伴随出现(无序)的及这2种关系的结合.这种相关事务集的划分和序关系的判断就是本文要研究的偏序关系模式,且利用并发事务与相关事务的联系和并发关系中隐含的符合偏序性质的关系,给出基于并发序列模式的偏序关系模式挖掘方法.偏序关系是对一组相关事务集及其上的序关系的描述,偏序关系模式挖掘是在事务序列数据库上发现事务间偏序关系的挖掘任务.并发序列模式[2]挖掘是一种在序列模式挖掘基础上发现序列间并发关系的挖掘任务,而在它基础上可以进一步挖掘偏序关系模式.目前未见与本文提到的挖掘偏序模式方法相同的相关文献报道.
1 并发序列模式
序列(Sequence)是由一组元素组成的有序表,即不同元素的有序排列,记作S=<s1,s2,…,sn>,其中sk(1≤k≤n)是一个元素.序列模式挖掘是挖掘频繁出现的有序事件或子序列[1].序列模式挖掘的侧重点在于分析数据间的前后序列关系.
并发序列模式是结构关系模式(Structural Relation Pattern)的一种,其含义可理解为,2个或多个序列模式在客户序列数据库中同时被足够多的客户序列所支持.详细概念及挖掘方法见文献[2].
并发序列模式包含2种关系,一是各序列内部的顺序关系,二是序列之间的并发关系.对并发序列模式中的任2个元素,如果它们同属于一个序列模式,则它们之间存在顺序关系;如果它们分别出现在不同的序列模式中,则它们之间存在并发关系.并发序列模式的这种特性使得可以基于并发序列模式进行偏序模式的挖掘.
2 偏序关系和偏序关系模式
2.1 有序关系与偏序关系序列
定义1 有序、偏序和全序.
有序[3](Orders)可以看成是一个由有序对组成的二元关系集合,可以应用集合操作来处理有序关系.
如果一个二元关系P⊂A×A是自反、反对称和传递的,则P是集合A上的偏序[4].即对于偏序关系P,有[3]
(1)自反性:对于所有的t∈A,有(t,t)∈P;
(2)反对称性:对于所有的t1,t2∈A,有(t1,t2)∈P和(t2,t1)∈P,当且仅当t1=t2时.
(3)传递性:对于所有的t1,t2,t3∈A,如果有(t1,t2)∈P且(t2,t3)∈P则有(t1,t3)∈P.
如果对于任意2个元素t1,t2∈A,有(t1,t2)∈P,则P是一个全序关系.
定义2 有序关系序列.
如果序列c是由互不相同的元素α1,α2,…,αn组成,且所处的位置分别是1,2,…,n,则所有元素之间都是有序的,称它们相对于c有序,表示为<α1,α2,…,αn>c,称c是一个有序关系序列.特别地,对于元素α和β,若它们相对于序列c有序,且出现次序是α在前β在后,则表示为<α,β>c或 <α,β>∠c,也可以省略表示为<αβ>.
单就一个序列来说,如果其中没有重复出现的元素,则将构成一个全序关系,即所有元素之间都有序.可以通过消去序列模式中重复元素的方法得到全序关系.
定义3 元素间的序.
设事务集I上的有序关系序列集A={s1,s2,…,sn},对于2个不相同的元素(事务)α,β∈I:
如果存在si∈A,使得<α,β>∠si,且对于任何sj∈A,或者<α,β>∠sj,或者α∉sj且β∉sj,称元素α,β相对于A是有序的;
如果不存在si∈A,使得α,β∈si,则称元素α,β相对于A是无序的;
如果存在si,sj∈A,且si≠sj,有<α,β>∠si和<β,α>∠sj,称元素α,β相对于A是次序矛盾的;
对于元素β∈I,如果存在α,γ∈I,si,sj∈A,且si≠sj,有<α,β>∠si,<α,β><sj和 <β,γ><si,<β,γ>∠sj,称元素β相对于A是次序不完全的.
定义4 序列对偏序关系的支持.
如果给定有序关系序列O和一个偏序关系P,O和P的元素即相同,而P的所有二元关系在O中都成立,则称有序关系序列O支持偏序关系P,或者说,O是P的一种全序表现形式、P可产生O,表示为O|→P.
一般地,如果序列S存在一个子序列O,O是一个有序关系序列,且O支持P,则称S支持P,或者说,S包含了P的一种全序表现形式、P可产生S的一个子序列,表示为S|→P.
2.2 偏序关系模式
构成偏序关系的所有元素属于一个集合,即它们之间有较强的关联关系.为衡量这种关系的强弱,引入相关度的概念.
定义5 相关度:对于基于事务集I中的序列数据库CSDB,元素α和β的相关度是指相对于α或β在CSDB的某一序列中出现,α和β同时出现的频度,形式地表示为:

一般地,对于元素α1,α2,…,αn的相关度可定义为所有包含α1,α2,…,或αn的客户序列中同时包含所有α1,α2,…,和αn的客户序列数的比例.即:
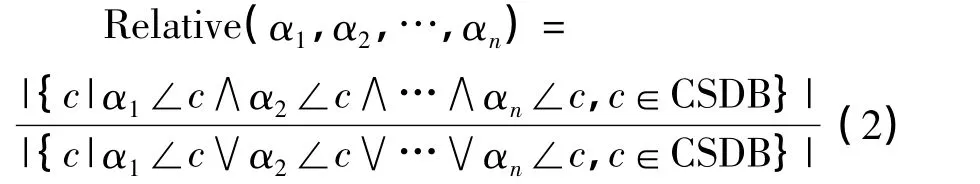
定义6 相关元素:对于基于事务集I中的序列数据库CSDB,如果元素α1,α2,…,αn的相关度足够大,即达到或超过了某一设定值minrel,即:Relative(α1,α2,…,αn)≥minrel,则称这些元素相对于序列数据库CSDB是相关的.特别地,如果对于元素 α和 β有Relative(α,β)≥minrel,则称α和β是相关的,表示为α||β.一般的,符号“||”表示前后两项之间是相关的.
上述提到的相关元素对和有序元素概念中涉及的minrel叫做最小相关度.
定义7 有序度:对于基于事务集I中的序列数据库CSDB,元素α和β的有序度是指相对于α或β在CSDB的某一序列中出现,α和β以<α,β>的次序同时出现的频度,形式地表示为:
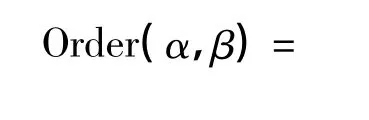
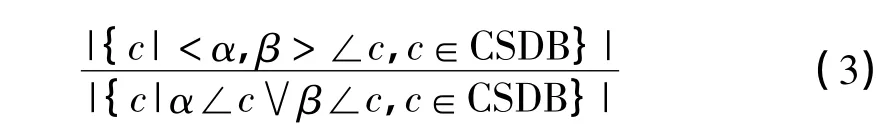
定义8 有序元素:对于基于事务集I中的序列数据库CSDB,如果元素α和β的有序度足够大,即达到或超过了某一设定值minrel,即: Order(α,β)≥minrel,则称元素α和β相对于序列数据库CSDB是有序的,它们构成一对有序元素,表示为α<β.一般的,符号“<”表示前后两项之间是有序的.
定义9 偏序关系模式.
对于基于事务集I中的序列数据库CSDB,一个偏序关系模式是指其上的一个相关元素集R以及该集合上的二元关系P,P是一个偏序关系,而每个二元关系中的两个元素都是CSDB的有序元素,且P在CSDB的序列中频繁地出现,即有足够多的序列支持P,称P是一个偏序关系模式.即:设用户给定的最小相关度为minrel,则
Relative(R)≥minrel;
P={<α,β>|Order(α,β)≥minrel,and α,β∈R};
P是偏序关系,且
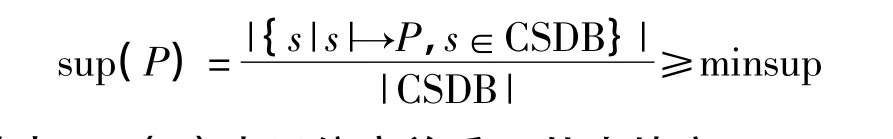
其中:sup(P)表示偏序关系P的支持度,minsup是用户指定最小支持度,表示P是频繁出现的,是一个模式.
3 偏序关系模式与并发序列模式
3.1 偏序关系模式的性质
对于序列数据库CSDB上相关元素集R的偏序关系P,α、β、γ是R的元素:
性质1 反单调性:R的子集R'上的二元关系P'仍是一个偏序关系模式,如果:
P'={<α,β>|α,β∈R',<α,β>∈P,R'⊂R}即:偏序关系模式的子模式仍是偏序关系.
性质2 相关性:R上的所有元素之间都是相关的.
性质3 交换律:α||β=β||α,即元素间的相关关系是相互的、对称的.
性质4 分配律:(α<β)||(α<γ)=α< (β||γ),(α<γ)||(β<γ)=(α||β)<γ,即:两个具有相同前驱(后继)的相关有序对,可以提取共同的前驱(后继).
分配律将在对偏序关系模式进行整理、组合、求精、优化过程中起到重要作用.
3.2 并发序列模式与偏序模式的联系
根据并发序列模式的定义和性质[2,5]与上述偏序关系模式的定义和性质,设最小相关度、最小并发度值相同,如果两个序列模式s1和s2是并发的,则可得到以下推论:
推论1 s1和s2的所有序列中的所有元素构成相关元素集;
推论2 分属s1和s2上的任意两个元素是相关的;
推论3 同属s1或s2上的任意两个元素之间是有序的;
推论4 如果s1或s2中无重复元素,那么s1或s2是有序关系序列.
定理1 有序关系序列集上的偏序关系.
对于事务集I上的有序关系序列集A={s1,s2,…,sn},如果A中不包含任何次序矛盾的元素对和次序不完全的元素,则A可构成一个偏序关系.
简要证明:A中不包含任何次序矛盾的元素对保证了反对称性;A中内部不包括次序不完全的元素保证了传递性.所以A可构成一个偏序关系.
定理2 由并发序列模式可得出偏序关系模式.
证明:首先根据推论1,并发序列模式的所有序列中的所有元素构成相关元素集,而偏序关系模式的基础是相关元素集;其次,根据推论4,如果并发序列模式的某个序列中无重复元素,那么这个序列是有序关系序列,即:若将所有并发序列模式的各序列中的重复元素去掉,可得到一组有序关系序列集;根据定理1,如果从前面得到的有序关系序列集中去掉那些包含次序矛盾元素对和包含次序不完全元素的序列,可得到一个偏序关系模式.
定理3 所有偏序关系模式可由并发序列模式导出.
证明:由于偏序关系模式要求在序列数据库中有足够多的客户序列支持P,而每个这样的客户序列将对应一个有序关系序列支持P.由于P是频繁的,则这些有序关系序列将构成一个并发序列模式.反过来说,这样的一个并发序列模式可产生给定的偏序关系模式.
由定理3可知所有偏序关系模式可由并发序列模式导出,定理2给出了由并发序列模式得出偏序关系模式的方法:首先,对并发序列模式的每个序列进行拆分,使之成为有序关系序列,得到有序关系序列集,详见算法1;其次,在有序关系序列集上消除包括次序相矛盾的元素对和次序不完全的元素的序列,详见算法2至4.
3.3 主要算法描述
(1)设定以偏序模式的最小支持度(minsup)为最小并发度进行并发序列模式挖掘,得到最大并发序列模式集CSPSet;
(2)对并发序列模式集CSPSet的每一个并发序列模式CSP;
(A)并发序列模式CSP中包含的所有元素构成关联元素集R;
(B)通过消除重复元素的办法拆分并发序列模式CSP的每个序列sp,得到一组有序关系序列opg,拆分过程见算法1,拆分后去掉有包含关系的序列.根据并发序列模式的性质,这些有序关系序列也是并发的.对CSP的所有序列拆分后得到一个并发的有序关系序列集COP;
(C)对COP进行重组,得到若干个新的有序关系序列集POP,使得每个POP中不包含次序相矛盾的元素对和次序不完全的元素,为已得到的每个偏序关系模式构造偏序关系图.过程见算法2~算法4;
(D)根据定理2,这些POP都是偏序关系模式.
算法1 拆分序列模式 //将含有重复元素的序列拆分成若干个无重复元素的有序关系序列.
输入:并发序列模式CSP
输出:有序关系序列集COP方法:
(1)令COP为空
(2)对于CSP中每一序列模式s做如下处理,直至CSP为空:
若s中存在某一重复出现的元素a,记录a重复出现的位置a1、a2、…、an和次数n,将s复制成n个序列s1、s2、…、sn,使该元素a在每个序列si中只出现在ai位置一次(i=1,2,…,n),其他元素不变,并存到CSP中;
否则,令 COP=COP∪{s},CSP=CSP-{s}.
(3)输出COP
算法2 构建偏序关系模式(POP_Graph).
输入:并发有序关系序列集COP={βi|βi∈SP,1≤i≤n,n是COP中有序关系序列个数}.
输出:偏序关系模式图(POP_Graph).
方法:
(1)为每一个有序序列(βi∈COP)构建序列模式图(SPG).每个SPG叫做一个偏序分支图(POBG),则有序序列βi的偏序分支表示为POBG(βi).
(2)POP_Graph=POBG(β1)∪POBG(β2)∪…∪POBG(βn).
(3)Call RefinePOP_Graph(POP_Graph).//求精构建最终的偏序关系模式图POP_Graph.
算法3 RefinePOP_Graph(POP_Graph)//对POP_Graph的求精.
输入:未求精的POP_Graph,用POPG表示.
输出:(the refined POPG)经组合后构成的偏序关系模式(POP_Graph).
方法:
(1)Call Combine(POBG(βi),POBG(βj)).对于任两个POBG(βi),POBG(βj)∈POPG,i≠j组合,得到一个新偏序分支图 POBG',如果POBG'不为空就存到POPG中.
(2)所有的可组合成新偏序分支图(新图不为空)的POBG'从POBGs中删除.
(3)重复步骤(1),(2)直到无新的偏序分支图要组合.
算法4 Combine将2个并发有序关系模式组合偏序关系模式.
输入:任意两个并发的有序模式图POBG (βi),POBG(βj).
输出:偏序关系模式.
方法:
(1)令POBG'为空
(2)如果(βi包含 βj)或(βj包含 βi),返回;
(3)如果(βi和βj包含次序相矛盾的元素对)或(βj和βi包含次序不完全的元素),返回;
(4)找出POBG(βi)和POBG(βj)的公共前缀,定义为preS.
(5)找出POBG(βi)和POBG(βj)的公共后缀,定义为postS.
(6)如果preS或postS不为空,令elemSi= (βi-preS-postS)和 elemSj=(βi-preS-postS);
(7)对 elemSi和 elemSj进行进一步求精(递归调用算法3);
(8)用有向边连接各部分构成偏序关系模式.
4 举例
在给定的序列数据库上挖掘偏序模式,且给定最小相关度minrel.步骤是先按最小并发度等于最小相关度进行并发序列模式挖掘,然后对每个并发序列模式应用算法得到偏序模式.
假设挖掘得到的一个并发序列模式为[<ebcb>+<eacb>+<efcb>+<fcbc>],以此为基础挖掘偏序模式,过程描述如下:
(1)首先,应用算法1对有重复元素的序列进行分解使之成为无重复元素的有序关系序列,则序列<ebcb>分解成2个序列<ebc>和<ecb>,<fcbc>分解成2个序列 <fcb>和<fbc>.原并发序列模式变成并发的有序模式[<ebc>+<ecb>+<eacb>+<efcb>+<fbc>+<fcb>].
(2)其次,去掉有包含关系的序列,由于序列<eacb>包含序列<ecb>,序列<efcb>包含序列<fcb>,则消除后,原并发的有序模式替换成[<ebc>+<eacb>+<efcb>+<fbc>].
(3)应用算法2~算法4可得到2个偏序关系模式,如图1所示.
其中相关元素:{a,b,c,e,f}相关关系如下:
①相关关系{<eb>,<ec>,<bc>,<fb>,<fc>}
②相关关系{<ea>,<eb>,<ec>,<ef>,<ac>,<ab>,<fb>}.
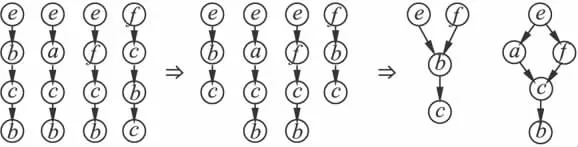
图1 从并发关系模式[<ebcb>+<eacb>+<efcb>+<fcbc>]生成偏序关系模式Fig.1 From concurrent pattem[<ebcb>+<eacb>+<efcb>+<fcbc>]to partial pattem
5 结束语
主要描述了基于元素间偏序关系的理论体系,分析偏序和并发的概念,给出有关偏序的定义,引入相关度、相关元素和偏序关系模式的定义,通过性质、定理推导出偏序与并发之间有着紧密的联系,在此基础上得出基于并发序列模式的偏序模式挖掘方法,并应用实例说明此方法的挖掘过程.本课题是把每个项集看作一个元素进行讨论.偏序关系模式挖掘具有实际的应用价值,这将是今后工作的重点研究方向.
[1] Gemma Gasas-Garriga.Summarizing Sequential Date with Closed Partial Orders[J].SIAM Conf,2005: 380-391.
[2] Chen Weiru,Zhang Yang,Chen Shanshan,et al.From Sequential Patterns to Structural Relation Patterns[C]//2009 International Conference on Scalable Computing and Communications;Eighth International Conference on Embedded Computing,Washington:IEEE Computer Society,2009:148-153.
[3] Antti Ukkonen.Data Mining Techniques for Discovering Partial Orders[EB/OL].(2004-10-31)[2010-12-17].http://users.ics.tkk.fi/aukkonen/pdf/aukkonen_thesis.pdf.
[4] 但红卫.基于偏序的频繁序列模式压缩算法研究[D].浙江:浙江大学,2007:37-65.
[5] Lu Jing,Chen Weiru,Osei Adjei,et al.Sequential Patterns Postprocessing for Structural Relation Patterns Mining[J].International Journal of Data Warehousing and Mining(IJDWM),2008,4(3):71-89.

