“动能定理”教学中的四点拓展

闫峰

(徐州市第一中学 江苏 徐州 221140)

1 “化曲为直、化变为恒” 思想的应用

人教版高中《物理·必修2》动能定理中通过“物体在恒力作用下做直线运动”的情境推导得到动能定理.对于变力作用、物体做曲线运动的情况教材没有深入讨论，只是做出了如下表述“当物体受变力作用，或做曲线运动时，仍可采用过去的方法，把过程分解成许多小段，认为物体在每小段运动中受到的是恒力，运动的轨迹是直线，这样也能得到动能定理.”那么究竟如何借助上述思想推导出动能定理呢？现从高中物理教学的角度尝试如下.

设一质点在平面内沿曲线路径由1运动到2，质点质量为m，所受合力为F.现将轨迹分为n小段，质点在每一小段内的位移称为元位移Δsi(i=1，2，…，n)，质点的运动可看作由许多元位移组成，如图1所示.

图1

解析：因为元位移Δsi很小，故可近似认为

(1)在Δsi内合力Fi(i=1，2，…,n)不变；

(2)Δsi的方向为该段位移起点处曲线的切线方向.

由(1)、(2)两步得

对上式求和

考虑到在曲线运动中vτ2=v2，且m为恒量，上式即为

或

该式表示的物理意义为“质点动能的增量等于作用于质点的合力所作的功”即动能定理.

2 质点系的动能定理及其应用

高中阶段主要是对单个质点使用动能定理，以至于不少教辅资料都将动能定理的研究对象表述为单个质点.实际上，如同牛顿第二定律，动能定理不但适用于单个质点，也适用于质点系，质点系动能定理的表述为“质点系动能的增量在数值上等于一切外力所作功与一切内力所作功的代数和”即

W外总+W内总=ΔEk.

【例1】如图2(a)所示，有一光滑的“T”形支架，在它的竖直杆上套有一个质量为m的物体a，用长为l的不可伸长的细绳将a悬挂在套于水平杆上的小环b下，b的质量也为m.开始时a处于静止状态，细绳处于竖直状态.今用水平恒力F=3mg拉小环b使a上升.求当拉至细绳与水平杆成θ=37°角时，a的速度为多大?

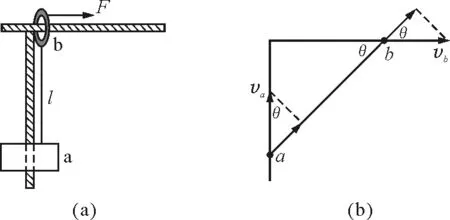
图2

解析：将a，b和绳看作质点系统.在外力方面，F做正功，a的重力做负功

W外总=Flcosθ-magl(1- sinθ)

在内力方面，绳与a之间、绳与b之间有相互的拉力作用，但相互拉力做功的代数和为零.由此可知本题中W内总=0.

由质点系动能定理得

因绳不可伸长，由图2(b)知

vasinθ=vbcosθ

解得

【例2】 a，b，c三物体由不可伸长的轻绳和两定滑轮连接，如图3(a)所示.体积很小的物体a叠放在平板b的右端，平板长l=0.4 m，物体的质量分别为ma=mb=1 kg、mc=2 kg，a，b之间以及b与水平桌面之间的动摩擦因数μ=0.25，整个系统从静止开始运动，求a滑离b时各物体的速度?(g=10 m/s2)

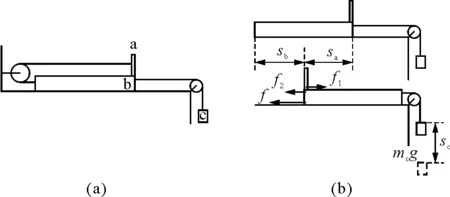
图3

解析：将a，b，c及轻绳看作一质点系统.如图3(b)所示，在外力方面，c的重力mcg作正功、桌面对b的摩擦力f作负功

W外总=mcgsc-fsb

在内力方面，a,b间的滑动摩擦力f1和f2都作负功、绳与a，b，c之间虽有相互的拉力作用，但相互拉力作功的代数和为零，W内总= -f1sa-f2sb.

因绳不可伸长，有

va=vb=vc=v

由质点系动能定理得

其中

f=μ(ma+mb)gf1=f2=μmag

sa=sb=sc=0.5l

解得

v=1 m/s

3 动能定理在非惯性系中的应用

由于动能定理是在牛顿运动定律的基础上推得的，因此只能在惯性系中使用.但是有些问题在惯性系中分析比较繁琐，而在非惯性系中考虑反而比较简单.那么在非惯性系中能否使用动能定理呢？在引入惯性力后，也可以在非惯性系中讨论质点动力学问题而保持质点动力学方程的形式不变，动能定理的形式是依然成立的，此时动能定理中的速度应理解为相对非惯性系的速度.

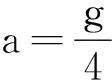
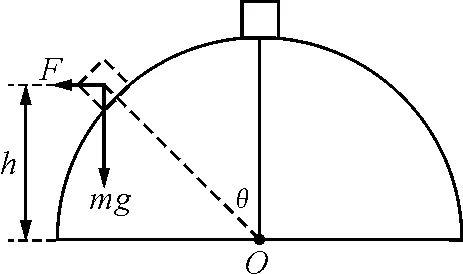
图4

解析：选半球体为参考系.设滑块刚离开半球体时的速度为v，滑块受到的惯性力为F.由动力学方程有

由非惯性系中的动能定理有

其中

解得

h=0.81R

4 赝动能定理及其应用

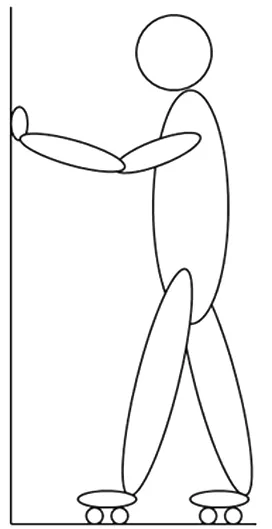
图5

如图5所示，穿无摩擦溜冰鞋的溜冰者站在水平地面上，用手推墙，使自己向后运动.溜冰者所受的外力(重力、地面和墙面对人的弹力)不做功，人获得的动能是内力做功的结果.但是没有外力是不能改变系统质心的运动状态的，即没有外力是不能改变质心平动动能的，那么外力和质心的平动动能间的定量关系如何呢？

外力对质点系的赝功定义为

式中Fi为作用于质点系的第i个外力，rC为质心的位矢.由此可得

上式表明“作用于一个质点系的合外力所作的赝功，等于该质点系质心平动动能的增量”这就是赝动能定理.赝动能定理能够帮助学生理解外力不做功时系统质心的平动动能如何改变，高中教学中向学生简单介绍还是有意义的.

【例4】如图6所示，把质量均为m的两个小钢球用长为2l的线连接，放在光滑的水平面上.在线的中点O作用一个恒定的拉力F，其方向沿水平方向且与开始时连线的方向垂直；连线非常柔软且不会伸缩，质量可忽略不计.经过若干次碰撞后，最后两个钢球一直在接触状态下运动，若此时绳中点的位移为s，那么系统因碰撞而失去的能量是多少?

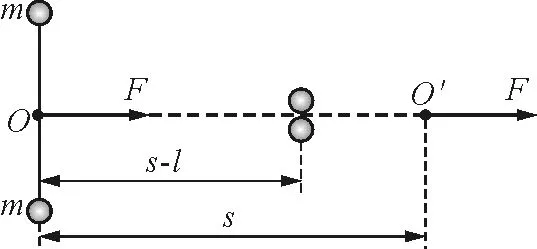
图6

分析：本题的关键是要求得两小球最后的共同速度，对绳球系统使用赝动能定理得

这里vC是系统质心的速度，当然也是最终两小球的共同速度；求得此速度后该题得到解决(以下略).

动能定理是高中物理的重点教学内容.在教学中教师如何适时渗透科学探究的思想、引导学生从多角度认识同一物理规律，笔者在此进行了粗浅的探索，欢迎大家批评指正.