“数形结合”是解决物理问题的有效方式
——“光穿过平行玻璃砖之侧移量”的一种简单定性解答
晏志武
(临沧市临翔区第一中学 云南 临沧 677000)
曾读一篇文章[1],文中介绍了 “光穿过上下表面平行的玻璃砖时发生侧移的量”的两种求解方法.作为长期从事高中物理教学的一线教师,笔者不赞同上述两种偏重数学推导,而冲淡其物理意义的解法(请参看原文).在此提出一种“数形结合”方法,既突出问题本身物理情景,所用数学知识又极其简单,且有“中学味”的定性解决办法,简述于下.
1 光侧移量
笔者认为,光侧移量是光的入射点与光的出射点的间隔距离,即图1中的AB.

图1
2 需要证明的两个前提
(1)入射角越大,入射角与折射角的差角i-r偏离法线越多,相同差角在玻璃砖中对应的底边越长.这是显而易见的,无须更多说明.
(2)随着入射角的增大,入射角与折射角的差角也增大.
证明:
设入射角为i,折射角为r,玻璃砖的折射率为n.
由折射定律
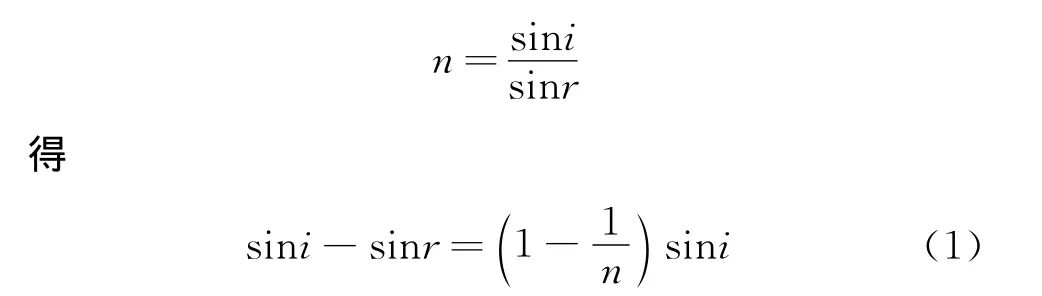
可见,sini-sinr随i而增大.
接下来证明,i-r又是随sini-sinr而增大.
如图2,将单位圆的半径等分为4份,O1B,O2C,O3D,OE分别表示4个角θ1=∠AOB,θ2=∠AOC,θ3=∠AOD,θ4=∠AOE的正弦值.

图2
显然

即在角度正弦值之差相等的情况下,角度越大,角度差也越大.实际情况是,角度正弦值之差越来越大,[上述(1)式]即可说明.也就是说
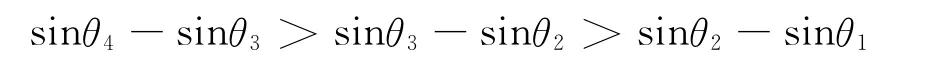
则θ4-θ3比θ3-θ2,θ3-θ2比θ2-θ1就会较正弦值之差相等时大得更多,“i-r随sini-sinr而增大”得证.
由以上易知,“i-r随i而增大”,前提(2)成立.以上两个前提得证,即入射角增大时,入射角与折射角的差角也增大,且差角偏离法线量增多.因此,光侧移量随着入射角的增大而增大.
3 结束语
物理学科与数学的联系是密切的,但也不能将解决物理问题等同于做数学题.物理情景怎样,物理意义如何,始终应该是教师和学生们摆在物理教学首位的东西.
1 余红岩.微元法在修正几何光学题中的应用.物理通报,2011(2):35~36

