基于DBBC+Mark 5B记录系统的脉冲星观测*

李志玄，汪 敏，郝龙飞，罗近涛

(1.中国科学院国家天文台云南天文台，云南 昆明 650011;2.中国科学院研究生院，北京 100049;3.中国科学院天体结构与演化重点实验室，云南 昆明 650011;4.中国科学院上海天文台，上海 200030)

云南天文台40 m射电望远镜配备有S和X波段馈源及S/X双波段(本振分别为1 600 MHz与9 100 MHz)致冷接收机。终端主要为基于ABBC+Mark 5A与基于DBBC+Mark 5B的两套VLBI终端。

脉冲星是一种具有高速稳定自转的天体，自转周期从约1.6 ms到几秒。大多数脉冲星在射电波段有连续的辐射，辐射谱服从幂律谱，在1 400 MHz处的辐射强度约为0.1 mJy到1 Jy［1］。由于脉冲星的辐射具有很强的方向性，且辐射轴与自转轴一般不重合，所以接收到的脉冲星辐射是周期性的脉冲，周期与脉冲星自转周期相同。通过对脉冲星周期和辐射的监测，可以开展很多天体物理与基础物理学方面的研究［2］。

脉冲星辐射在到达望远镜时受到星际介质的影响有色散、散射和法拉第旋转。其中，散射与法拉第旋转效应相对较弱。色散效应是指不同频率的电磁波经过星际介质后产生的延迟不同，从而到达望远镜的时间也不同，它与观测频率、带宽及色散量(DM，Dispersion Measure)有关。色散效应会导致所看到的脉冲星轮廓展宽，当色散延迟与脉冲星的周期相当甚至远远大于脉冲周期时，就得不到脉冲轮廓。所以，在进行脉冲星观测时通常都要进行消色散处理。消色散算法一般分为非相干消色散与相干消色散两种。其中实现非相干消色散的系统有滤波器组，如乌鲁木齐天文站的2(偏振)×128(通道)×2.5 MHz(单通道带宽)多通道滤波器组［3］; 自相关频谱仪，如 Caltech FPTM［4］(Fast Pulsar Timing Machine)。实现相干消色散的系统有基带记录系统(Baseband Recording System)，如澳大利亚的Parkes射电望远镜配备的CPSR2［5］(the second Caltech Parkes Swinburne Recorder)相干消色散系统。

本文采用基带记录系统和相干消色散方法。对数据进行消色散和作适当平均之后，得到时域数据流。然后将得到的时域上的数据流存储为文件，以备进行各种处理。文中所提及的有周期折叠获得平均轮廓，直接作图得到单个脉冲图像，按不同的折叠时间得到的轮廓的信噪比各量与时间的关系。通过这些分析，证明40 m天线在现有终端设备条件下可以开展一些脉冲星观测研究。

1 观测系统与观测流程

1.1 观测系统

观测采用基于DBBC+Mark 5B记录系统的VLBI终端，系统结构及信号流程如图1。

图1 系统结构与信号流程Fig.1 Block diagram of the observation system

射频信号由天线接收进入馈源，经过接收机后，分两路中频信号(分别为S、X波段)至中频分配器，然后进入两个中频自动增益控制单元(AGC，Automatic Gain Controller)，经A/D转换后，由数字下变频器将中频信号转换为基带信号，最后通过VSI接口输出到Mark 5B记录器，将信号记录到磁盘阵列。

1.2 观测流程

观测时，首先打开FS控制计算机，按所需仪器设置编写过程文件控制文件，在此选择4个S波段(BBC05～BBC08)通道上边带，每个通道带宽为8 MHz，本振分别为606.99 MHz，614.99 MHz，622.99 MHz，630.99 MHz;采样率为16 MHz，2 bits量化。接着用FS计算机控制DBBC与Mark 5B，并进入FS环境，载入过程控制文件，使所有终端设备准备就绪，然后打开天线驱动器及控制系统，让天线跟踪所要观测的脉冲星，最后在FS计算机上控制Mark 5B使之开始(结束)记录，这样，数据就按照过程控制文件里所设置的模式记录在Mark 5B的硬盘组里。然后，由数据回放命令将数据取至Mark 5B主计算机硬盘里，或是直接通过网络传送到数据处理计算机硬盘中。

2 数据处理及结果分析

2.1 色散效应与相干消色散方法

当电磁波经过星际等离子体时，会产生延迟效应，延迟量为:

其中vg为电磁波在等离子体中的群速;d为源到地球的视向距离;c为光速。vg可由下式求得:

其中μ为等离子体的折射率;f为电磁波的频率;fp为等离子体的特征频率，且:

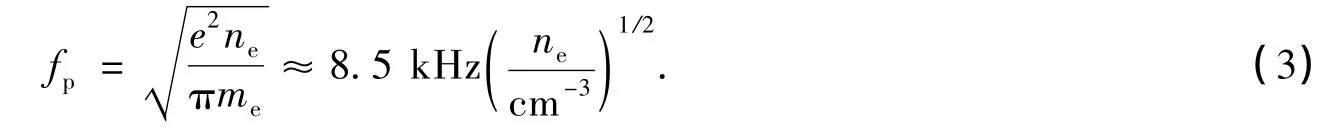
式中ne为星际介质电子柱密度，cm－3为所取单位(下同)，me为电子质量。这样代入 (1)式即得:

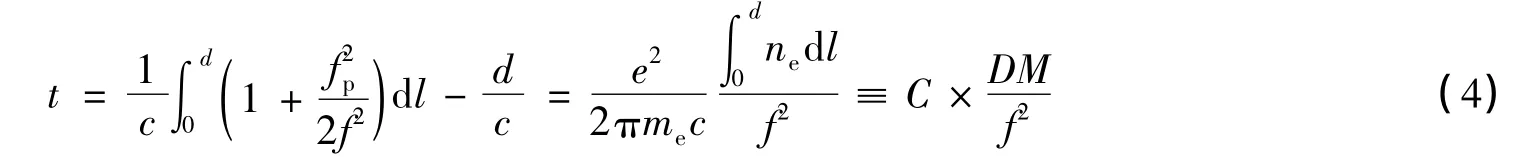
式中C为常数，

DM称为色散量:

一般取其单位为pc/cm3。由以上各式，可得两不同频率的电磁波经过等离子体时，所产生的色散延迟差为:

由于此效应，脉冲星信号的不同频率成分到达天线的时刻也不同，于是导致脉冲宽度展宽失真，甚至完全观测不到脉冲信号。

相干消色散算法就是将所接收到的信号进行快速傅里叶变换(FFT)到频域，然后将频域上的各频点的信号乘一个相应的相位因子以达到时域平移目的，再反变换到时域，实现将不同频率成分的信号对齐到某一个频点以消除色散效应。这里，相移规则由一个Chirp函数［6］表示:

式中f0为所选基准频率;f为电磁波频率与基准频率的差fx－f0。数据变换到频域后，与上式相乘即可实现所需相移。

2.2 相干消色散的实现及平均轮廓的获取

数据的相干消色散及求得平均轮廓的算法如图2，由C语言实现，编译环境为Linux下的gcc编译器，FFT(Fast Fourier Transform)及IFFT(Inverse Fast Fourier Transform)由FFTW函数库来实现，程序在一台普通台式计算机上运行。解码时须参照Mark 5B的数据格式(Mark 5B System User's Manual，MIT Haystack Observatory，August2006)以及观测时所使用的过程控制文件来选择解码设置，并显示帧头信息，如同步字、所在帧的记录起始时刻，这样不但可以了解程序运行的进度，更重要的是可以检验程序的解码部分是否正确。作平均是为了在允许的时间分辨率下尽量增加积分时间，以提高信噪比。本文中涉及到的有关PSR J0835-4510的数据，采取4096点的平均，时间分辨率为4096/16 MHz=0.256 ms，这样一个周期内约有349个点;PSR J0332+5434的数据，取8 192个点的平均，时间分辨率为0.512 ms，一个周期内约有1 395个点。进行平均后，将平均所得到的数据写入一个文件并将其存储起来，以备下一步的处理。

首先，可以按周期折叠相加得到脉冲星的平均轮廓。所谓折叠相加，就是将数据依次取为许多小段，每段数据长度为一个脉冲周期，然后将这些小段依次点对点叠加。要注意的是，一般情况下一个周期内数据的点数并不为整数，若将点数向下取整，则每取一段就会产生小数位个点的误差，当此误差累加到大于1的时候，在取下一段的时候向后跳过一点，这样就能保证误差不大于一个采样点，得到平均轮廓如图3。其中观测频率及带宽为2206.99 MHz+32 MHz，折叠数据总时长为10 min，观测时间分别为MJD 55145(PSR J0835-4510)和MJD 55165(PSR J0332+5434)。折叠周期选取为修正(见2.3节)后的视周期。

图2 相干消色散处理程序流程Fig.2 Flowchart of the algorithm of the coherent de-dispersion

图3 PSR J0332+5434与PSR J0835-4510的平均脉冲轮廓Fig.3 The mean pulse profiles of PSR J0332+5434 and PSR J0835-4510

2.3 由平均轮廓展宽对视周期进行修正

由于台站坐标、钟差等的影响，按理论算法求得的视周期与实际的视周期会有一定差别。这就会导致折叠所得的轮廓变宽，且易知变宽的程度与折叠次数(或积分时间)成正比。所以可根据变宽的程度 Δt，和积分时间 tint作出修正［7］:

其中ptrue为真实视周期;p为初始折叠所用周期即由计算所得的视周期; +对应向右展宽Δt，－对应向左展宽Δt，如图中所示为向右展宽，则取+。修正的过程及效果见图4。

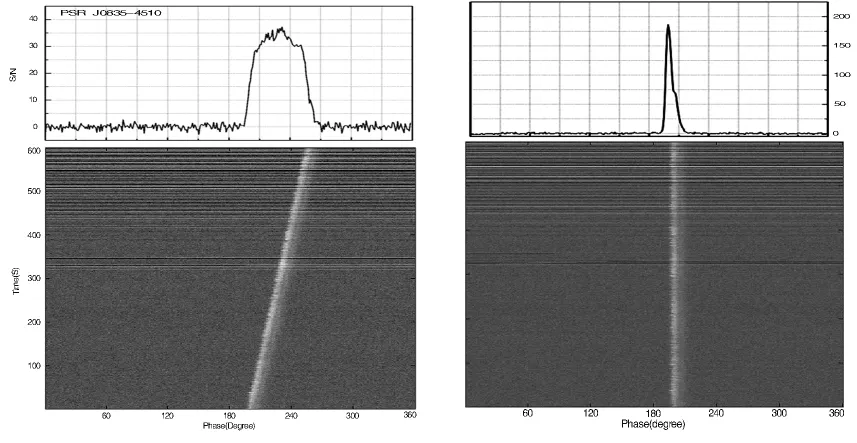
图4 PSR J0835-4510视周期的修正Fig.4 The improving process for the pulse period of PSR J0835-4510

图中灰度图为将600 s的数据按10个周期为一组，分为673组，然后将每组数据按周期折叠，从下至上分别对应的时间段为从前到后。左图为进行周期修正之前的，易知每组数据的轮廓所在位置在向右漂移，即对应总的轮廓的向右展宽(左上)，而总的漂移的时间即为(9)式中的Δt，由此即可得到修正后的周期ptrue，右图为修正后的结果。

2.4 PSR J0332+5434的单个脉冲

若将时域上数据直接画出，可得到单个脉冲的图像(图5)。由图可明显的看出周期性信号，且经计算易得其周期约0.714 s与脉冲星周期相符。其他与平均值偏离较大的点为随机干扰。

图5 PSR J0332+5434的单个脉冲Fig.5 Single pulses of PSR J0332+5423

2.5 结果及分析

根据前面提到的折叠获得脉冲星平均脉冲轮廓的原理，可知若假定观测中脉冲星的流量稳定，干扰较少，且系统性能稳定时，则轮廓的信噪比仅与折叠次数也即用来折叠的数据的时长有关，且

因为若以每次用来折叠的Np个点(一个脉冲周期)为一组数据，由于噪声的随机性，则各组数据中噪声部分可视为相互独立的，这样经过n次点对点相加(即折叠)后，噪声的均方根(r.m.s.)可大致认为是每单个组数据的倍，而脉冲信号则是单个脉冲信号的n倍，于是S/N应正比于而n=tint/Np，所以可得到(10)式所示关系。实际观测的信噪比与时间的关系图如图6。

图6 (a)噪声r.m.s.－tint (b)PSR J0835-4510平均轮廓S/N－tintFig.6 (a)The relation between the r.m.s.of noise and the integration time(b)The relation between the SNR of the mean profile of PSR J0835-4510 and the integration time

两图中虚线均为函数f(t) =t1/2×Const的曲线，可见虚线与实线是大体上符合的。由于短时间内脉冲星的流量一般有较高的稳定度，则由上面两图可知，在此次观测的10 min内系统是比较稳定的。

3 结论

通过对这两颗流量较强的脉冲星的观测和数据处理，初步证实昆明站40 m射电望远镜系统是能够开展脉冲星观测研究的。就所观测的两颗源来说，数据的信噪比已经达到作进一步研究如计算TOA的要求。而且对类似PSR J0332+5423的脉冲星，还可以做一些单个脉冲方面的研究。但由于系统灵敏度相对较低，数据的信噪比还是很低，于是需要加大带宽和提高观测系统其他方面性能来提高信噪比，同时为了得到一些流量较小的源的平均轮廓，还需要加长观测时间来提高轮廓信噪比，这样就会产生更多的数据，大量的数据对后期软件处理的计算机系统的速度要求也相应提高，并行处理将成为必不可少的工具。

致谢:由衷感谢北京大学吴鑫基教授给予的脉冲星理论与观测技术方面的指导，乌鲁木齐天文台艾力·伊沙木丁老师在数据处理方面提供的帮助。感谢云南天文台施硕彪、许春在天线和观测系统整体运作方面的大力协助。

［1］Manchester R N，Hobbs G B，Teoh A，et al.The Australia Telescope National Facility pulsar catalogue ［J］.Astron J，2005，129(4):1993－2006.

［2］J H Taylor，D R Stinebring.Recent Progress in the Understanding of Pulsars ［J］.Ann Rev Astron Astrophys，1986，24:285 －327.

［3］N Wang，R N Manchester，J Zhang，et al.Pulsar Timing at Urumqi Astronomical Observatory;Observing System and Results［J］.MNRAS，2001，328(3):855－866.

［4］Navarro，Jose.A Wide Bandwidth Pulsar Timing Machine ［D］.PhD Dissertation，California Inst of Tech Pasadena，CA United States，1994.

［5］A W Hoton，M Bailes，S M Ord.High-precision Baseband Timing of 15 Millisecond Pulsars［J］.MNRAS，2006，369(3):1502 －1520.

［6］Jenet F A，Cook W R，Prince W R，et al.A Wide-Bandwidth Digital Recording System for Radio Pulsar Astronomy ［J］.PASP，2001，109:707－718.

［7］D R Lorimer，M Kramer.Handbook of Pulsar Astronomy ［M］.Cambridge University Press，2005:168－170.