随机行走的扩散方程

焦潍苹,李宏亮

(1.潍坊工商职业学院信息工程系,山东诸城262200;2.浙江外国语学院理工学院,浙江杭州310012)

扩散方程的物理模型一般是气体的扩散,液体的渗透,布朗运动等,而在这里我们将建立一个随机行走模型来得到扩散方程.

1 随机行走模型

我们假设一个粒子作一维的随机行走,它只有两个运动方向,向左或向右.我们假设粒子在x轴上运动,初始位置在原点.设其每次移动的长度为δ,xi为一随机变量,并且令

设每一步都是独立的,P(xi=δ)=p,P(xi=-δ)=q,由于粒子只有向左或向右移动两种可能,因此p+q=1(见文献[1]).第n步粒子所在的位置为应用二项分布,在给定的步数后粒子在某个固定位置的概率是确定的.但我们更感兴趣的是,当δ→0,步数n→时,该随机行走问题的连续极限,然而我们不是要确定这个问题的确切的解,而是通过确定随机变量Xn的数学期望与方差来研究这个问题,随机变量Xn数学期望得到的是n步之后粒子在的平均位置,而方差得到的是实际位置偏离平均位置的程度.我们先考虑离散的情况.

2 期望与方差

2.1 离散型随机变量的数学期望

定义2.1 (见文献[3])设离散型随机变量x的分布律为P(xk)=pk,k=1,2,….若级数随机变量x的数学期望,记为E(x),即

定理2.2

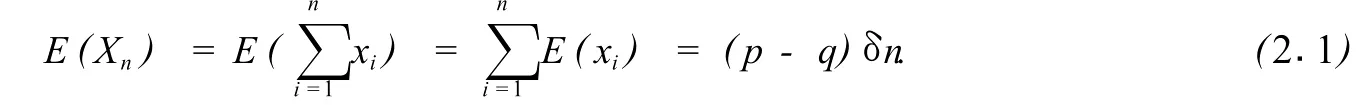
证明 对于上述随机行走模型中的粒子在第i步移动后,随机变量xi的期望为E(xi)=(+δ)P(xi=δ)+(-δ)P(xx=-δ)=(p-q)δ.E(x)为关于x的线性函数,因此我们有

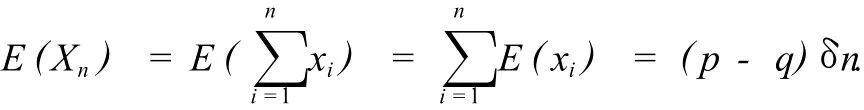
2.2 离散型随机变量的方差

定义2.3 设x是一随机变量,若的方差E[(x-E(x))2]存在,则称E[(x-E(x))2]为x的方差,记为D(x)(见文献[3]).

定理2.4

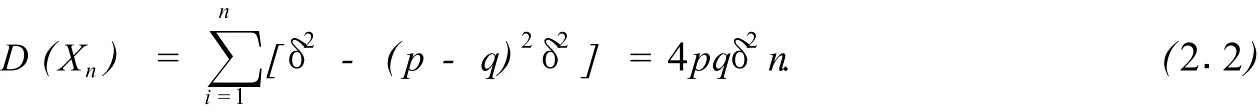
证明 由方差的定义我们可得方差的计算公式D(x)=E(x2)-[E(x)]2,对于独立随机变量X和Y有D(X+Y)=D(X)+D(Y)(见文献[3]),这样我们可得独立随机变量和的方相互独立的随机变量,i=1,2…,n,有

又因为p+q=1,所以

3 差分方程

假设该随机行走模型满足:

(i)单位时间内粒子移动r步;

(ii)粒子在t=0时刻,由x=0处开始移动;

(iii)粒子移动n步的时间为t,且其移动n步后的位置在x处.

定义3.1 设v(x,t)为t时刻粒子在x位置的概率分布,这里t=nτ,即v(x,t)=P(Xn=x).

定理3.2

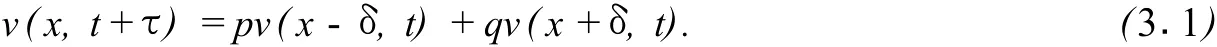
证明 由定义3.1知v(x,t+τ)为在(t+τ)时刻粒子在位置x的概率,v(x-δ,t)为t时刻粒子在位置x-δ的概率,v(x+δ,t)为t时刻粒子在位置x+δ的概率.又因为粒子只有向右和向左两个移动方向,所以在(t+τ)时刻粒子在位置x的概率为t时刻粒子在位置x-δ的概率乘以向右移动的概率p在加上t时刻粒子在位置x+δ的概率乘以向左移动的概率,即v(x,t+τ)=pv(x-δ,t)+qv(x+δ,t).

又p+q=1,因此应用泰勒级数将v(x,t+τ)及v(x±δ,t)在点(x,t)处展开得:

代入(3.1)式得差分方程:

4 扩散方程

布朗运动是小颗粒的无规则运动.布朗运动最初是由英国生物学家布朗于1827年根据观察花粉微粒在夜面上做“无规则运动”的物理现象而提出的,爱因斯坦于1905年首次对这一现象的物理规律给出了一种数学描述,使得这一课题有了显著发展.布朗运动作为具有连续时间参数和连续状态的一个随机过程,在其它许多领域有着十分重要的应用,如物理、经济、通讯理论、生物、管理科学和数理统计等(见文献[2]).

本文提出的随机行走模型可用于一维的布朗运动,给定一个粒子,由假设(i)其在一个给定的单位时间里有r次碰撞发生,每一个碰撞假设是独立的且给定一个大小为δ的位移,假设向右移动的概率为p,向左移动的概率为q.对于我们的随机行走模型,r步之后,粒子在位置Xr,由(2.1)及(2.2)知,粒子在位置Xr的期望与方差为E(Xr)=(p-q)rδ,D(Xr)=4pqδ2r.实验上,在液体或气体中(一维运动)的粒子平均速度为c,方差为D＞0,根据假设每单位时间内有r次碰撞(r不是一个试验结果,而是假设很大).

因为布朗运动是连续的,我们必须考虑当δ→0,r→时的极限,设c和D是极限过程中的定值(见文献[1]).

证明 由(4.1)知,当δ→0,r→时,有E(Xr)=(p-q)δr→c,D(Xr)=4pqδ2r→D.如果当→D＞0矛盾.因此当δ→0,r→时,必须有

定理4.2 当δ→0,τ→0时,(3.3)式的极限为微分方程

此方程为一维扩散方程.

本文从一个随机行走的模型出发,利用期望与方差及泰勒展式,得到了一个一维的扩散方程,这个方程与布朗运动有着紧密联系,更有助于理解渗透与扩散的实质.同时这个方程的得到过程也揭示了概率与分析之间有着密切的联系.该方法也可用于更加复杂的随机运功动情况,有待于进一步的研究.

[1]Zauderer E.Partial differential equations of applied mathematics.2nd edition[M].New York:John W iley&Sons,Inc,1989:891.

[2]黄新,李俊锋.布朗运动的扩散方程[J].湖南城市学院学报:自然科学版,2010(3):45-46.

[3]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008:90-103.