水下加肋双层圆柱壳体振动传递特性分析

金广文，章林柯，缪旭弘，贾 地，王雪仁

(1.中国人民解放军92537部队，北京 100161;2.海军工程大学 振动与噪声研究所，武汉 430033)

水下加肋双层圆柱壳体振动传递特性分析

金广文1，章林柯2，缪旭弘1，贾 地1，王雪仁1

(1.中国人民解放军92537部队，北京 100161;2.海军工程大学 振动与噪声研究所，武汉 430033)

研究水下双层圆柱壳体振动传递特性具有重要的工程意义，尤其对于水下结构噪声快速预报和外壳表面速度场实时重构。以此为出发点，通过双层加肋圆柱壳体模型水下振动试验研究了不同激励条件下内外壳体振动特性;然后建立了水下双层圆柱壳体有限元模型，计算分析了壳体在流固耦合条件下的振动路径及特性，找出了不同激励方向、流体耦合方式和内外壳体连接方式等典型因素下内、外壳体间振动传递规律，为速度场重构和水下噪声预报提供了一定的理论指导。

速度场;圆柱壳体;振动传递;流固耦合;振动试验

研究像潜艇这样的水下双层圆柱壳体结构噪声快速预报技术具有重要的现实意义，双层壳体结构在系统激励下最终由外壳体振动激励外场水介质形成辐射声场，因而要预报圆柱壳体水下噪声有必要先重构出系统激励下的外壳体表面振动速度场。流固耦合作用下的双层圆柱壳体结构振动传递路径非常复杂，主要决定于系统的激励特性、内外壳体间连接方式和边界条件等因素。可见，有必要从重构这种复杂结构壳体表面速度场出发研究内外壳体结构声传递规律，此外该研究对水下圆柱壳体结构噪声源识别和声学故障定位等研究也具有重要的指导意义。针对水下复杂的双层圆柱壳体结构，国内外许多学者对无限长和有限长双层加肋圆柱壳体的振动及声辐射特性进行过比较深入的研究［1～3］，但从壳体表面速度场重构出发深入研究其内、外壳体振动传递规律的报道还很少见。文献［4］重点研究了空气中双层圆柱壳体结构的振动路径和特性，本文就是在此基础上通过水下振动试验和有限元数值计算相结合的方法，研究水下双层圆柱壳体振动传递特性。

从工程上来说，通过试验研究振动传递特性最可信，但代价会很大，也很难研究不同因素对振动传递特性的影响。因此本文先设计了一个典型的双层圆柱壳体模型进行试验分析，然后根据试验模型建立有限元分析模型，并用试验结果对有限元分析结果进行验证。在此基础上，在改变有限元计算模型的不同参数，分析不同影响因素下的振动传递特性。

1 水下双层圆柱壳体速度场重构理论

水下双层加肋圆柱壳体结构的传递路径非常复杂，重构外壳体表面速度场最直接的工程方法就在壳体上布置大量传感器获取其振动响应，但由于外壳体内外都充满水介质，要布置大量湿端传感器的工程实施难度非常大。现实的工程方法可以考虑在机座和内壳体上布置大量传感器监测壳体振动状态，并根据内壳体测点信号实时重构出外壳体表面速度场。文献［5］已经给出了基于这种工程方案的双层圆柱壳体速度场重构方程:

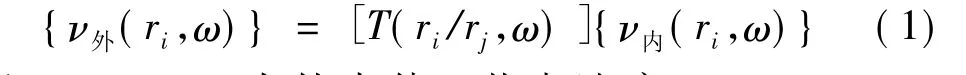
这里 ν外(ri，ω)为外壳体 i节点速度，i=1 ～N;ν内(ri，ω)为内壳体第 i个振动测点振速，i=1～M;［T(ri/rj，ω)］为内壳体测点与外壳体速度场之间的振动传递矩阵，即传递率矩阵。这里振动传递率的定位为在指定激励下内外壳体振动响应比值，它与激励位置、内、外壳体响应点位置、方向都有关，随结构动力学特性和边界条件变化而变化。

式中［H内(ri/pj;ω)］H和［H外(ri/pj;ω)］H分别为内、外壳对激励P的频响函数矩阵，“+”表示M-P广义逆。可见只需实时测得内壳测点的振动信号就可以重构出外壳体表面速度场，其关键就是要预先得到内、外壳体振动传递矩阵［T(ri/rj，ω)］，而［T(ri/rj，ω)］又决定于壳体结构振动传递路径、激励特征、内外壳连接方式、以及流固耦合边界条件等因素。可见，有必要从这几方面入手深入研究双层加肋圆柱壳体振动传递特性，以指导建立准确的振动传递矩阵及重构模型。

以此为出发点，本文用水下振动试验研究和理论计算方法相结合的方法分析壳体振动传递规律，以及不同因素对双层壳体传递特性的影响，为水下双层圆柱壳体表面速度场的重构以及水下辐射噪声的预报提供一定的理论指导。

2 水下双层圆柱壳体振动试验研究

为了研究双层圆柱壳体在水下的振动传递特性，本文进行了双层圆柱壳体缩比模型的水下振动试验，模型结构及主要尺寸如图1所示，用两个电磁激振器在图示机座板位置进行激励，内、外壳分别布置2个和3个加速度计测量振动响应。试验在120 m×80 m×4 m的水池中进行，模型吃水0.9 m，见图2。试验测量采样频率为1 kHz，采样时间10 s，参考速度5×10－8m/s。

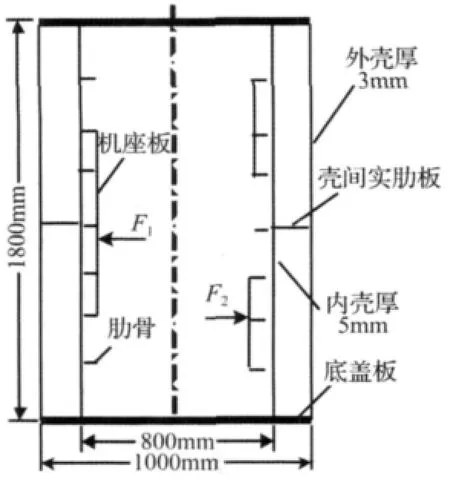
图1 双层圆柱壳体模型Fig.1 Schematic diagram of submerged cylindrical double-shell model

图2 水下振动试验现场Fig.2 Underwater vibration test locale

分别用白噪声和双点稳态信号激励壳体，得到的内外壳体振动响应曲线如图3和图4所示。从图3可以看出在激励点附近的机座板振幅明显大于其它位置;壳体中间位置激励(F1)下外壳体的振动传递率明显大于端部处激励(F2)，这是因为壳体两端盖板刚度较大，可见壳体速度场重构时更应该关心中部位置的激励源;同样可以得出中部位置的噪声源比端部噪声源更容易定位和识别。由图4同样可知机座板上振幅明显大于内外壳体，而内壳振幅整体又比外壳大。内、外壳体振动线谱基本一致，尤其是在低中频段耦合较强，可见速度场重构的测点应该优先考虑内壳体，而不是机座;而进行噪声源识别时也应该重点考虑内、外壳体间的耦合。

3 水下结构振动有限元数学模型

而为了进一步分析不同参数和条件对水下结构振动传递特性的影响，采用有限元分析进行数值计算是一种有效而经济的方法［6］。根据波动理论，流体的波动方程:

式中:p为瞬时声压;t为时间变量;c为声速。

对上式进行有限元离散，用矩阵形式表示为:

同理，含有阻尼的弹性结构振动的有限元矩阵方程为:

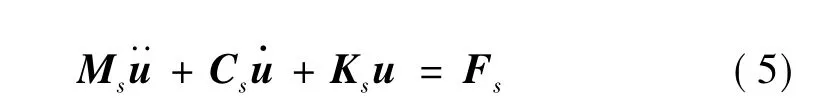
式中:Ms为结构的质量矩阵;Ks为结构的刚度矩阵;Cs为结构阻尼矩阵;Fs为结构载荷力向量。

当弹性结构置于声学介质中时，在流体与结构的交界面上流体与结构之间存在着相互耦合作用，声压对结构产生一个面力的作用。根据虚功原理可将该面力等效移置到单元节点上，于是，弹性结构与声场的耦合振动矩阵方程为:

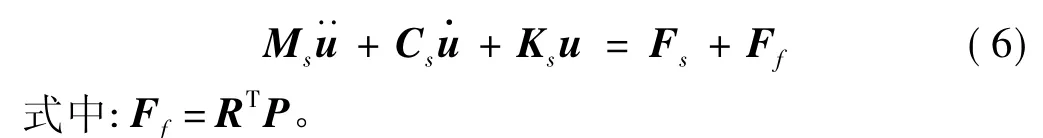
联立(4)、(6)两式，即可得到流固耦合系统统一的运动方程:

根据以上有限元理论，建立典型水下双层加肋圆柱壳体结构模型，见图1，在内外壳体间增加了实肋板的数量，双层壳体间和外场充满流体。假设圆柱壳两端为满足自由边界条件，结构振动响应在线性范围内，流体满足线性声学条件。流体为无粘无旋可压缩的，密度为 ρf=1 000 kg/m3，声速 c0=1 500 m/s。内外壳体、肋板材料一致，密度 ρs=7 800 kg/m3，弹性模量 E=210 GPa，泊松比v=0.3。对壳体进行有限元离散，整个模型划分了11 527个单元，其中壳体单元4 800个。

4 不同因素下的壳体振动传递特性分析

根据以上计算模型，用有限元分析软件ANSYS对壳体结构进行单点激励下的振动响应分析。由前面传递矩阵［T(ri/rj，ω)］的定义可知，矩阵的内的每个元素实际上反映了内、外壳体在指定激励下的传递率，因此下面主要就内外壳体振动传递率进行分析。

4.1 圆柱壳体振动传递路径分析

进行完全浸没在水中模型的谐响应分析，典型位置内、外壳体对应点位移幅值线谱如图5所示，图中下标“r”和“θ”分别代表径向和周向。从图中可知此时壳体在1 150 Hz下内、外壳体、肋板径向振型基本一致，可见低中频段内，内、外壳体、肋板之间的耦合作用比较强。进一步分析壳体结构的振动响应特征，发现计算结果得出的规律上节的试验分析结果基本一致，可见通过本文建立的有限元计算模型可以有效计算典型双层圆柱壳体的振动传递规律。

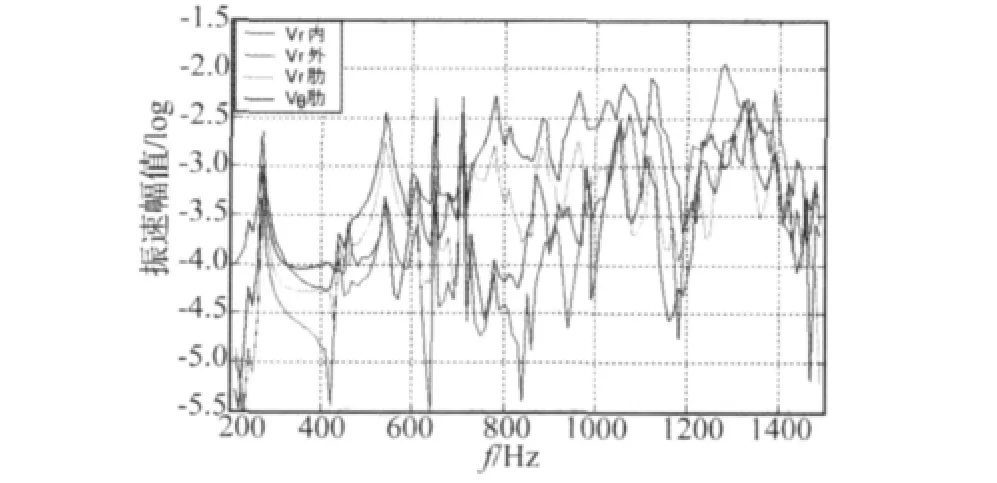
图5 水中内壳—肋板—外壳振动路径上响应线谱Fig.5 Vibration response on path of vibration transmission

而对比计算结果与试验曲线发现，在低中频段计算结果的外壳体振幅明显偏低，内、外壳体振幅差距较试验结果偏大，这主要是因为计算模型是完全浸没水下，而试验是半潜，且计算模型增加了壳间实肋板数量，这都使壳体结构的刚度增加，从而使外壳体振动幅值偏小，这将导致计算结果中内、外壳体振动传递率偏小。在高频段，内、外壳体、肋板振动幅度相差不明显，这主要是因为高频内外壳体耦合减弱，壳体以局部振动为主。

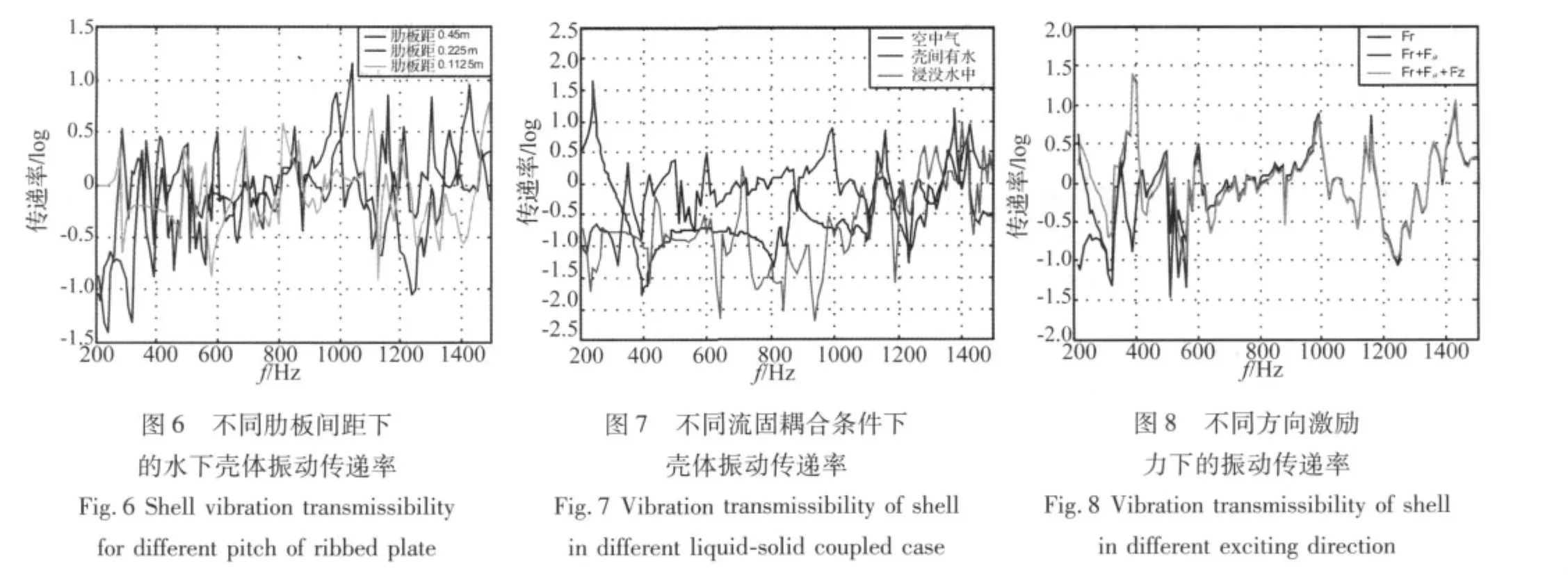
4.2 肋板间距振动传递路径的影响

为了分析壳体间连接方式对振动传递率的影响，对比不同肋板距下的内、外壳体振动传递率，见图6。图中传递率定义为外壳体中部典型位置与内壳体中部典型位置之间的振动响应比值，根据前面分析结果，内外壳体振动方向都取径向。从图中可以看出不同肋板距对壳体振动传递率频谱特征及幅值大小影响都较大，从总体趋势看来肋板距越密传递率越低，这是因为肋板距变密厚壳体结构刚度增大，使壳体振动幅度减少，尤其是外壳体(外壳体板厚较小对结构刚度更加敏感)，从而使内、外壳体振动传递率变小。

4.3 流固耦合作用对传递特性的影响

为了分析流固耦合条件对内外壳体振动传递特性的影响，又建立了空气中模型和双层壳间充满水的模型(此时外场无水)。分析空气中、壳间有水、浸没水中的内外壳体振动传递率，见图7。从图中可知流固耦合对低中频的壳体振动传递率影响较大，而对高频段(大于1 100 Hz)影响不太明显。比较空气中和水中的传递率，可知两层壳体间增加了水的传递作用后，中频段(320 Hz～1 100 Hz)内外壳振动传递率明显增强;而完全浸没在水中时，传递率又明显降低，此时外壳体内外都受到水压的影响，可见外场流体对振动传递率有很强的抑制作用。

4.4 不同方向激励力对传递特性影响

工程上分析壳体振动响应时，往往只考虑了机座板上径向激励。为了分析机座板上周向激励和轴向激励对内外壳体传递率的影响，对比了不同激励方向下的内外壳体振动传递率，见图8。分析结果可知，考虑了周向激励和轴向激励后，壳体振动传递率在550 Hz以上几乎没有影响，但在低频段影响相对较大。因此研究低频段内外壳体振动传递关系时必须考虑周向和轴向激励。

5 结论

综上所述，速度场重构时应该重点关注壳体中部激励源，重构方案中测点位置应该偏重于内壳体上。进行速度场重构和噪声源识别时，传递路径上应该重点考虑内壳体和肋板径向振动，尤其是低中频段内。流固耦合作用、壳体间肋板连接尺寸对内外壳体振动传递特性影响较大，中高频段内壳体周向和轴向的激励作用对内外壳体传递特性影响较小，但在低频段内不可忽略。可见，外壳体速度场重构工程实施时应该重点考虑激励点位置、测点布置、壳体间的不同连接方式，以及低中频段内流固耦合作用的影响，而对内壳体机座板上周向和轴向激励只须考虑其在低频段内的振动传递。

［1］ Yoshikawa S，Williams E G，Washburn K B.Vibration of two concentric submerged cylindricalshells coupled by the entrained fluid［J］.J.Acoust.Soc.Am.，1994，95(6):3273－3286.

［2］吴文伟，吴崇健，沈顺根.双层加肋圆柱壳振动和声辐射研究［J］.船舶力学，2002，6(1):44－51.

［3］陈小宁，李 宁，骆东平.潜艇舱段结构静动力性能有限元分析［J］.武汉理工大学学报(交通科学与工程版)，2003，27(5):674－677.

［4］金广文，何 琳，姜荣俊.基于速度场重构的双层圆柱壳体振动传递特性试验研究［J］.振动与冲击，2007，26(10):180－183.

［5］金广文，何 琳，姜荣俊.基于频响函数求逆法的双层圆柱壳体速度场重构［J］.振动与冲击，2007，26(8):60 －63.

［6］徐张明，汪 玉，华宏星.船舶结构的建模及水下振动和辐射噪声的 FEM/BEM 计算［J］.船舶力学，2002，6(4):89－95.

Vibration transmissibility of a submerged cylindrical double-shell based on reconstructing velocity field

JIN Guang-wen1，Zhang Lin-ke2，MIAO Xu-hong1，Jia Di1，Wang Xue-ren1

(1.People's Liberation Army.Beijing 100161，China;2.Research Inst.of Vibration ＆ Noise，Navel Univ.of Engineering，Wuhan 430033，China)

In order to reconstruct velocity field and evaluate noise on outer shell surface of a submarine，vibration transmissibility between double shells of a submerged cylindrical double-shell structure was studied with underwater vibration test.An finite element model of a ribbed cylindrical double-shell was established here，its vibration response was analyzed.The law of vibration transmissibility for cylindrical double-shells in different forms was found，with typical influencing factors of fluid-structure coupling，exciting forces and connection condition between double shells.The results of tests and calculations provided some theoretical basis for velocity field reconstruction of outer shell and noise source identification of a submarine.

velocity field;cylindrical shell;vibration transmissibility;fluid-structure coupled;vibration test

O327

A

博士后科学基金资助(200904061463);博士后科学基金(200904061463，201003763);国家自然科学基金资助(50979111)

2009－11－23 修改稿收到日期:2010－02－17

金广文 男，博士后，1978年生