埋置块式基础地基阻抗函数的简化计算方法研究

胡灿阳，陈清军，徐庆阳，熊琴琴

(1.南京审计学院 江苏省公共工程审计重点实验室，南京 210029;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

埋置块式基础地基阻抗函数的简化计算方法研究

胡灿阳1，2，陈清军2，徐庆阳1，熊琴琴1

(1.南京审计学院 江苏省公共工程审计重点实验室，南京 210029;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

目前关于地基阻抗的分析和计算方法都比较繁琐，不易为工程设计人员所掌握。基于此，提出了埋置基础地基阻抗函数的简化计算方法。首先，采用锥体模型分析均质半空间内埋置圆盘一维振动波的传播过程，得到了平动和转动时的地基阻抗。在此基础上，利用埋置圆盘组来模拟埋置基础，分析得到了埋置基础地基阻抗函数。最后，通过算例表明此方法计算效率高，误差小，适用于工程计算。

锥体模型;块式基础;阻抗函数;埋置基础;土－结构相互作用

土－结构动力相互作用是新近发展起来的与多学科相互交叉和渗透的学科，描述其动力学行为的数学模型(通常为一组控制方程)十分复杂。由于实际问题的复杂性和计算过程的繁琐性，使得这些模型不便用于实际工程中。近年来，一种采用锥体模型求解土－结构相互作用中地基阻抗函数的方法，因其简便性和实用性，受到了重视，但这一方法目前尚处于起步阶段，需要做进一步的研究。

锥体模型最早是由Ehlers［1］在1942年提出，最初用它来分析明置圆盘的平动，继而也用它分析转动。Gazetas［2］和 Gazetas 和 Dobry［3］使用楔形体和锥体来阐述二维和三维情况下的辐射阻尼。Meek和Wolf使用锥体模型得到了均质半空间表面基础动力响应的简便计算方法。他们又分别计算了刚性基岩覆盖层表面基础的动力响应，分析了柔性基岩覆盖层表面基础的动力响应。1993 年，Meek 和 wolf［4］利用 Boussinesq 等理论详细说明了锥体模型的物理意义，讨论了利用锥体模型代替弹性半空间的可行性，从而消除了众多学者对锥体模型的疑虑。此外，2002年，Jaya和 Prasad［5］使用了同样的截头锥段研究了层状土内埋置基础的动力刚度。然而，这种截头锥段法也存在缺陷，它的主要问题是:当低频时，阻尼系数会变成负值，这在物理上是不可能的。文献［6］对于锥体模型的初步应用有详细地总结。2003年，Pradhan等［7］利用波在锥中的传播，计算了层状土表面圆形基础的动力阻抗，这就克服了利用上面截头锥段分析时的缺陷。2008年，Pradhan等［8］利用锥模型对于层状土表面机器基础振动进行了分析，并同时进行了实验研究，通过对比，验证了锥体模型对于机器基础振动分析的有效性。目前，国内对锥体模型的研究较少，张剑寒等［9，10］基于锥体模型概念，得到了层状半空间地基上明置基础阻抗函数的计算方法，并与薄层法进行对比来研究它的精度。

1 埋置圆盘

可以把地基－基础接触面看作一个无质量刚性板，下面的均质半空间地基近似看作具有不同顶点高度z0的截头半无限弹性锥体，分为平动和转动锥体，表面圆盘相对应的锥体模型顶高半径比等参数以及平动锥模型与转动锥模型中波反射系数和相应的阻抗函数见文献［6］。

对于埋置在均质半空间里的半径为r0，埋深为e的圆盘，利用锥模型可以得到阻抗函数S(ω)的闭合解。先分析如图1所示竖向自由度的情况。使用双边锥模型，每个初始锥的动力刚度都相同。圆盘的初始位移幅值(ω)与圆盘上的作用力幅值 P0(ω)的关系为［11］:

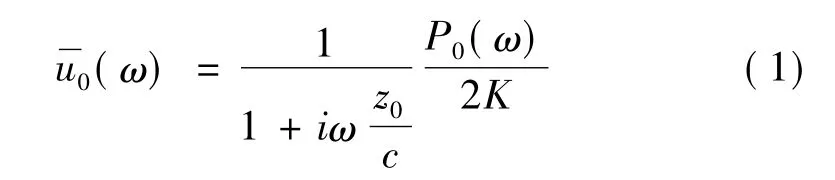
式中:K是半空间表面圆盘的静刚度系数;c是圆盘振动波传播速度，对于水平振动和扭转振动用剪切波速，对于竖向振动和扭转振动用胀缩波速;ω为频率。

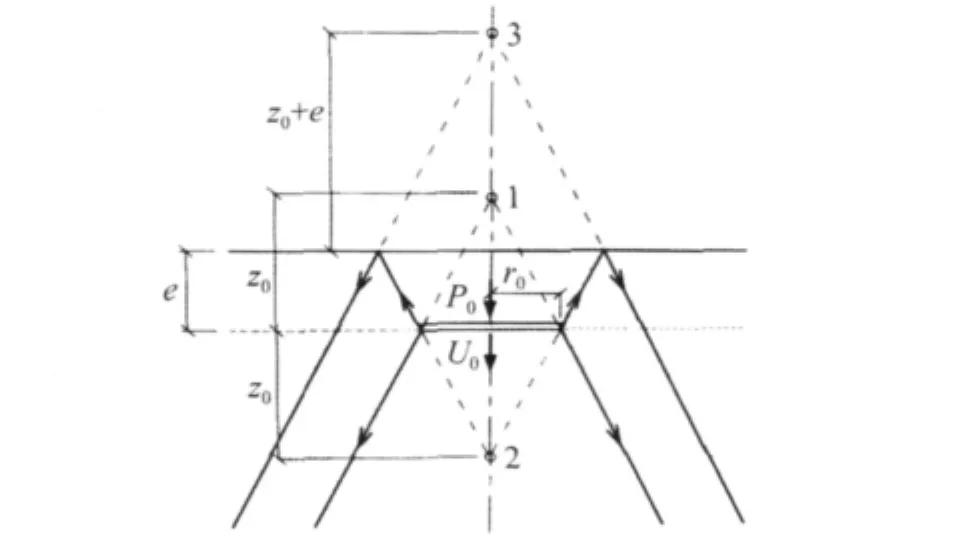
图1 埋置在均质半空间里圆盘波传播过程Fig.1 Wave propagation from disk embedded in homogeneous half-space

波在圆盘下面的初始锥内(顶点为1)向下传播，没有反射波产生，锥的张角也即顶点高半径比z0/r0，可以通过均质半空间表面圆盘的锥模型静力刚度系数与相应的用三维弹性理论求得的半空间上圆盘的静刚度精确解相等求出［6］，不同的平截锥具有不同的张角。波在圆盘上面的初始锥内(顶点为2)向上传播时，在自由表面产生反射，自由表面处入射波幅值为:

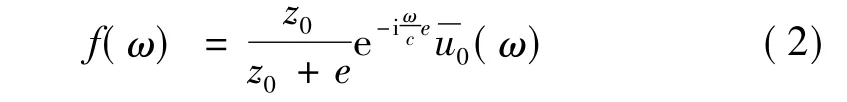
在自由表面处，反射系数 －α(ω)=1，反射波幅值为:

反射波在顶点为3的新锥内传播。当它传播到圆盘所在深度时，幅值衰减为:

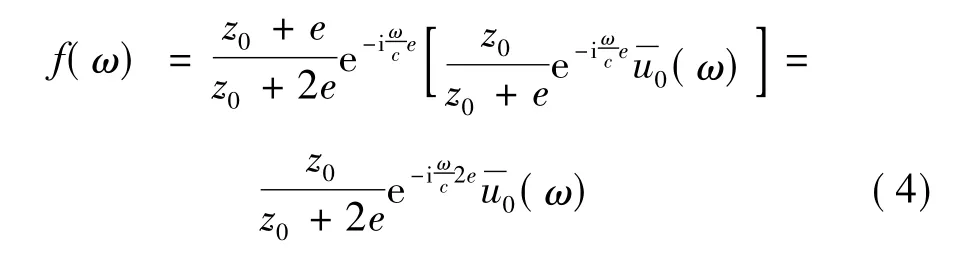
因为半空间是均质的，这个波会继续在截头锥内向无限远处传播，而不再产生反射。圆盘处的总位移u0(ω)是由这个反射波［式(4)］和原始激励波［式(1)］叠加而成的。于是有幅值:

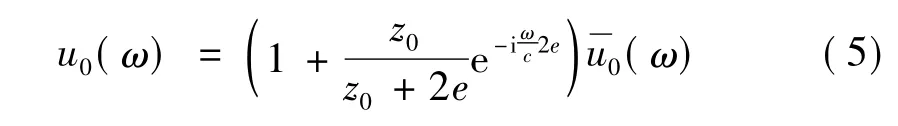
引入几何参数k=2e/z0和传播的时间参数T=2e/c，后得到:

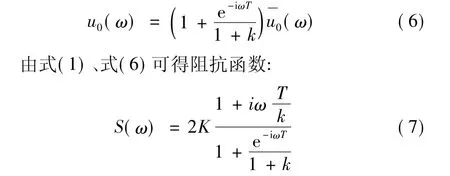
式(7)也即为平动锥的阻抗函数，对于水平振动和竖向振动，分别取相应的K、T和k进行计算。

对于转动自由度，分析过程是类似的。埋置在均质半空间里的圆盘地基阻抗函数:

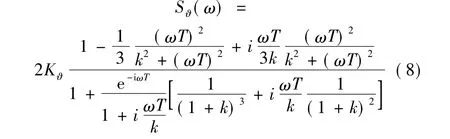
同样，对于摇摆振动和扭转振动，取相应的Kϑ、T和k进行计算。

2 埋置圆盘组

如图2所示，为了表示在半空间里半径为r0，深度为e的圆柱形基础，可以在基础位置处放置m个圆盘。也就是说，在以后将要开挖的地方可以看作是m个圆盘和其中的 m－1个分层。第一个圆盘在层状半空间的表面，第 m个圆盘在埋置基础的刚性基底处。文献［5］建议两个相邻圆盘的最大竖向间距Δe应该满足以下要求:每个波长度内至少要分为6层。

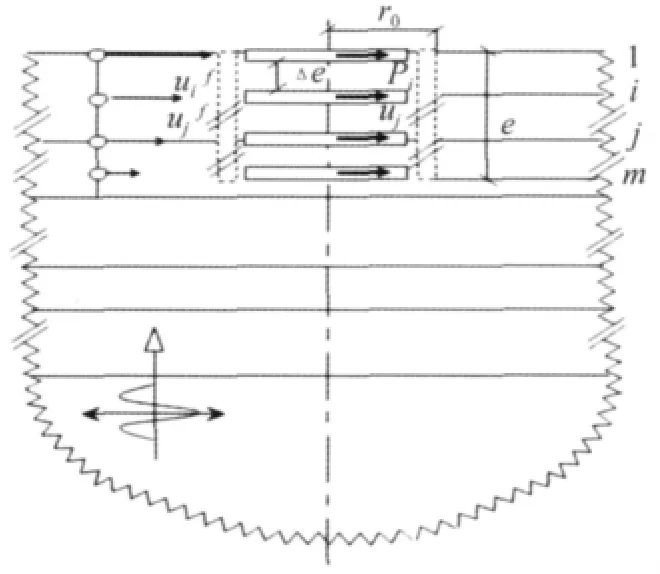
图2 半空间内埋置圆盘组Fig.2 Stack of disks to represent cylindrical foundation embedded in half-space

为了精确，本文采用每个波长度内要分为10层，波长为λ=c/(ω/2π):

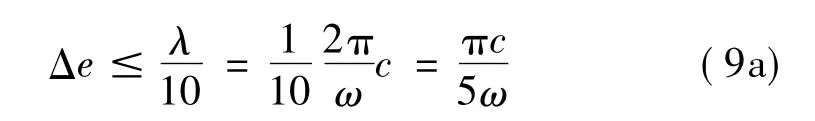
式中ω代表了动力模型的最高频率，c是波速(通常是剪切波速cs)。当使用无量纲频率a0=ωr0/cs时，有:

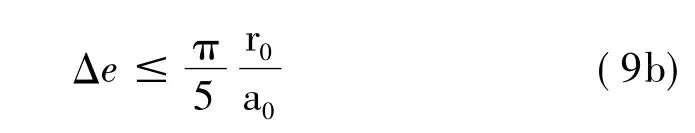
对于竖向自由度(图3)，有:

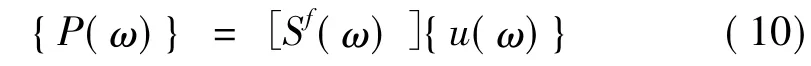
式(10)给出了埋置在未开挖的层状半空间内圆盘的力－位移关系，这里［Sf(ω)］是指与自由场圆盘组有关的阻抗矩阵。在自由场中，幅值为{u(ω)}的竖向位移分量之间是相互独立的。在刚性基础中，各点的竖向位移和基底的竖向位移相同，幅值都为u0(ω)。这种刚体位移表示为:

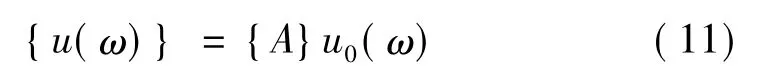
运动约束矢量{A}={111…1}T。力Q0(ω)等于各个荷载Pi(ω)之和:

则，由式(10)、式(11)、式(12)得:

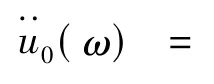
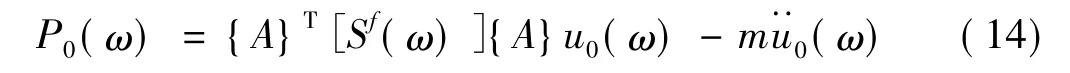
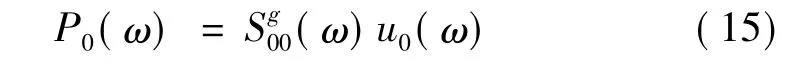
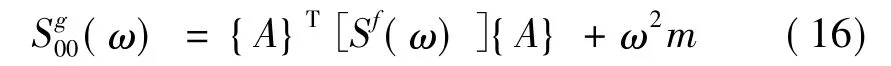
扭转自由度的分析过程类似，埋置基础地基阻抗是:

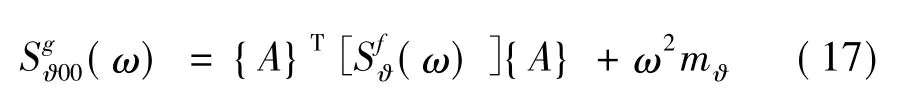
这里mϑ是开挖区域的质量极惯性矩，{A}和上面定义相同。

图3 竖向自由度时刚体位移和相互作用力Fig.3 Enforcement of rigid-body displacement for verticaldegree of freedom

分析耦合水平和摇摆自由度(图4)。埋置圆盘的水平位移幅值{u(ω)}和转动幅值{ϑ(ω)}都和基底的刚体运动相关，基底的水平位移幅值为{u0(ω)}，转动幅值为{ϑ0(ω)}，则有:

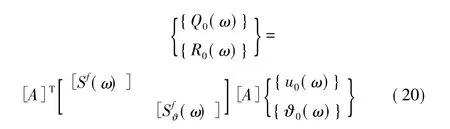
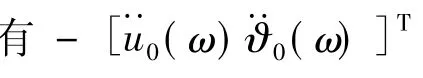
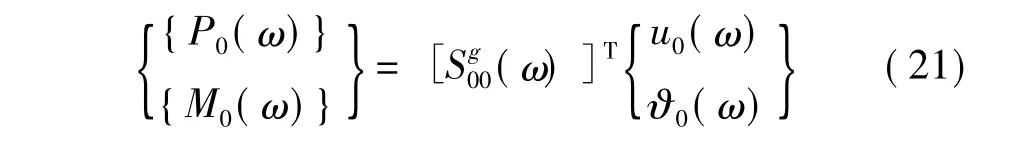
于是有埋置基础的阻抗函数矩阵:

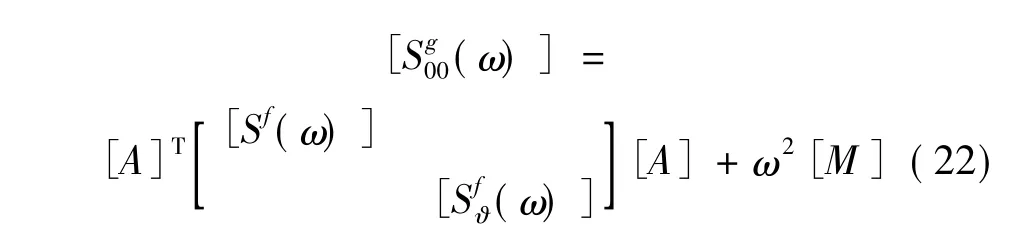
对上面的过程很容易进行一定的扩展。比如，当基础墙没有刚度和刚体约束时，矩阵［A］不再需要了。在这种情况下，位移和转动幅值［u(ω)］和［ϑ(ω)］都是未知的，由这些自由度来确定埋置基础的地基阻抗函数。圆盘中间的区域仍然通过对内部域的动力刚度矩阵进行抽取进行分析。后者是(上标e表示开挖):

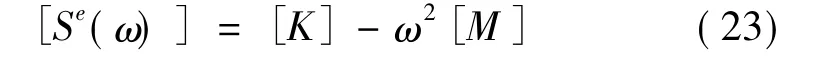
其中，［K］和［M］分别为开挖部分相应于{u(ω)}和{ϑ(ω)}的静力刚度矩阵和质量矩阵，可以通过将内部域模型化为具有竖轴的杆或者梁得到。修改后的相互作用力－位移关系为:

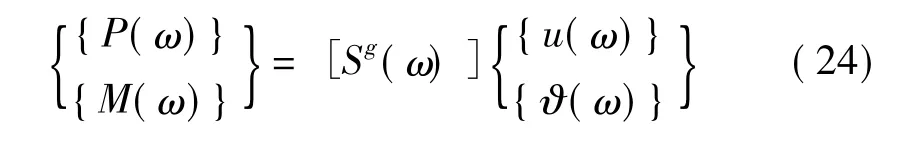
埋置基础的地基阻抗函数矩阵等于自由场阻抗矩阵与开挖部分刚度矩阵的差:

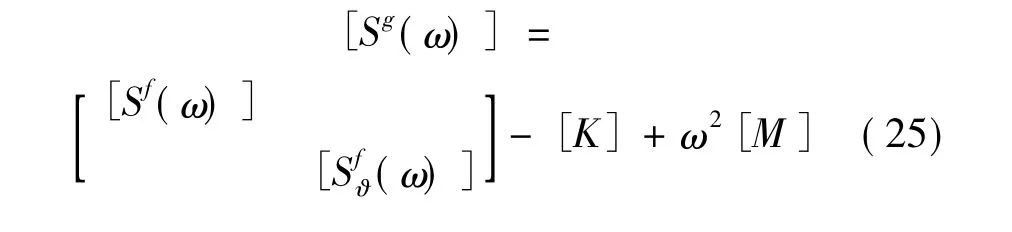
3 算例

如图5所示，在泊松比为υ=0.25的均质半空间里，有半径为r0埋置深度为e的刚性圆柱基础，计算它的所有自由度的阻抗函数。埋深率e/r0分别为0.5、1和2(这个范围包含了大多数实际工程的情况)。结果根据无量纲频率a0=ωr0/cs范围从0到4来确定。

由式(9b)可知两个相邻圆盘的最大竖向距离为Δe=(π/20)r0，这时a0=4。对于最大埋深率e/r0=2时，至少要分为13层，也就是要14个圆盘。本文使用16层，因此 Δe==0.125r0。同理，当 e/r0=1 时，模型分为8层，当e/r0=0.5时，模型分为4层。

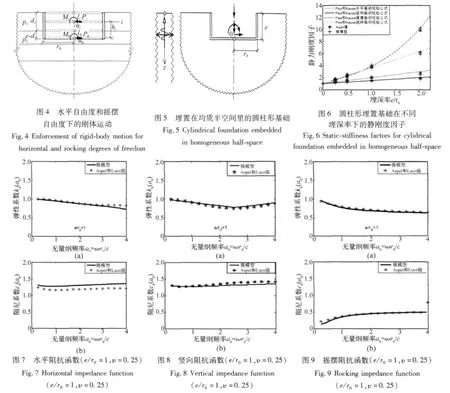
使用锥模型时，埋置基础静力刚度系数的计算也可以用同样的过程，这时ω=0。它们除以相同运动下明置基础的相应静力刚度系数，得到无量纲的静力刚度因子，并且在图6中和文献［12］的数值解进行对比。图6中的曲线相应于文献［13］中的经验公式，它适用于e/r0≤2，由图上可见锥模型的精度对于所有自由度都是很好的。

图7到图10给出了水平、竖向、摇摆和扭转运动阻抗函数对应于无量纲频率a2的弹性系数和阻尼系数。由图上可见，水平运动时，动力弹性系数的锥模型结果与文献［12］的数值解在低频部分吻合很好，在高频部分存在很小的偏差，动阻尼系数的锥模型结果与文献［12］的偏差不超过10%，在竖向、摇摆和扭转的情况下，锥模型的结果与文献［12］的值吻合的很好(这里是埋深率e/r0=1的情况，也可以在其它情况下进行比较)。由此可见，使用锥模型分析均质半空间里的埋置基础阻抗函数具有很高的精度。

图10 扭转阻抗函数(e/r0=1，υ=0.25)Fig.10 Torsional impedance function(e/r0=1，υ =0.25)

4 结论

本文首先基于锥体模型，对振动波在锥段内的传播进行分析，得到了埋置无质量刚性圆盘的地基阻抗函数。进而用一组埋置圆盘来模拟埋置基础，可以得到地基阻抗函数。最后，通过算例表明，此方法物理意义明确、分析和计算过程简单，结果具有很高的精度，适于工程人员掌握和应用。

［1］Ehlers G.The effect of soil flexibility on vibrating systems［J］.Beton Eisen，1942，41(21/22):197 －203.

［2］Gazetas G. Simple physical methods for foundation impedance.Dynamic behaviour of foundations and buried structures［M］.In:Banerjee PK，Butterfield R，editors.Developments in soil mechanics and foundation engineering，vol.3.London:Elsevier，1987.［chapter 2］.

［3］Gazetas G，Dobry R.Simple radiation damping model for piles and footings［J］.Journal of Geotechnical Engineering，ASCE，1984，110(6):937 －956.

［4］Meek J W，Wolf J P.Why cone models can represent the elastic half-space［J］.Earthquake Engineering and Structural Dynamics，1993，22(1):759 －771.

［5］Jaya K P，Prasad A M.Embedded foundation in layered soil under dynamic excitations［J］.Soil Dynamics and Earthquake Engineering，2002，22(6):485 －498.

［6］Wolf J P.Foundation vibration analysis using simple physical models［M］.Englewood Cliffs，NJ:Prentice-Hall，1994.

［7］Pradhan P K，Baidya D K，Ghosh D P.Impedance functions of circular foundation resting on layered soil using cone model［J］.Electronic Journal of Geotechnical Engineering，2003，8(B).

［8］ Pradhan P K，Mandal A，Baidya D K，et al.Dynamic response of machine foundation on layered soil:cone model versus experiments［J］. Geotechnicaland Geological Engineering，2008，26(4):453 －468.

［9］张剑寒，蒋 通.层状地基上块式基础地基阻抗函数简化计算方法［J］.工业建筑，2007，37(8):68－72.

［10］张剑寒，刘志杰，蒋 通.层状地基对块体基础地基刚度的影响［J］.工业建筑，2008，38(s1):664 －666.

［11］ Meek J W，Wolf J P.Cone models for embedded foundation［J］.Journal of Geotechnical Engineering Division，ASCE，1994，120(1):60－80.

［12］ Aspel R J，Luco J E.Impedance functions for foundations embedded in a layered medium: an integralequation approach［J］. Earthquake Engineering and Structural Dynamics，1987，15(2):213 －231.

［13］ Pais A， KauselE. Approximateformulasfordynamic stiffnesses of rigid foundations［J］.Soil Dynamics and Earthquake Engineering，1988，7(4):213 －227.

Simplified calculation method for impedance function of embedded block foundation

HU Can-yang1，2，CHEN Qing-jun2，XU Qing-yang1，XIONG Qin-qin1

(1.Nanjing Audit University，Jiangsu Key Laboratory of Public Project Audit，Nanjing 210029，China;2.State Key laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China)

Analysis and calculation methods for impedance function of a foundation are complicated，and it is difficult for engineering designers to grasp and use them.A simplified method was proposed here to calculate impedance function of a foundaton embedded in a half-space.Firstly，based on a cone model，one-dimensional vibration wave propagating of a rigid massless circular disk embedded in a homogeneous half-space was analysed.Impedance functions of translational and rotational cone models were derived.Then，the embedded foundation was modeled with a stack of disks and its impedance function was calculated.The model was validated by comparing the results with the rigorous analysis ones. The numerical results indicated that this method has higher precision and efficiency，it is applicable for engineering calculation.

cone model;block foundation;impedance function;embedded foundation;soil-structural interaction

TU470+.3

A

科技部国家重点实验室基础研究资助项目(SLDRCE08－B－03);江苏省高校自然科学研究项目(10KJB560003);江苏省高校优势学科建设工程资助项目(PADD)

2009－12－21 修改稿收到日期:2010－04－06

胡灿阳 男，博士，讲师，1974年1月生